行测-数量关系：1. 代入排除法、倍数特性法、方程法

本文主要是介绍行测-数量关系：1. 代入排除法、倍数特性法、方程法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1、代入排除法

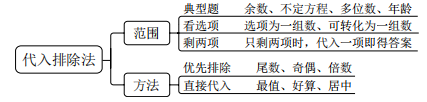
例题

A

D，设姐姐 x 岁，x - 3 - 4 > 0，x > 7

B，快速方法，$(18+余数{)}^2=361$

C

B

2、倍数特性法

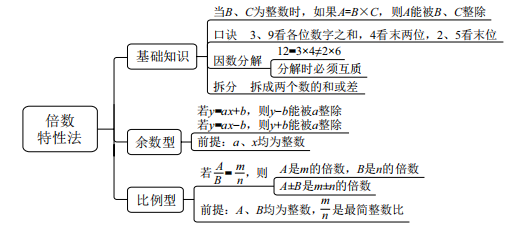
2.1 基础知识（整除型）

B

A，能被 9 整除那么被除数所有位数加起来为 9。

2.2 余数型

C，x - 70 能整除 50

B

D

D

2.3 比例型★★★

3，5，8，2

m 和 n 互质指的是 m 和 n 没有公约数。

A，全书一定是七的倍数。

C，总人数是 25 的倍数。直接看百分数更为简便，如果用常规方法需要列方程组。

C

B，全部出警次数肯定是 40 的倍数，带入选项求全部的次数即可。或者求乙是 7 的倍数，代入 95 - 甲的次数也能求得。

A = 13N，B = 20N，C = 39N，D = 50N，E = 5N，F = 4N，G = 7N，H = 10N

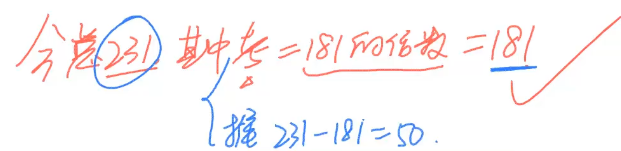
C

B

整除判定基础知识

3、方程法

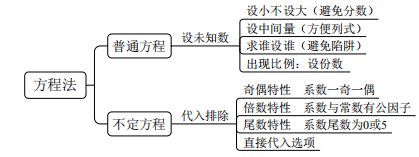
3.1 普通方程

C

B，设乙为 7x，总数为 40x，95 + 140 = 7x + 40x

3.2 不定方程

3.2.1 奇偶

B，x 一定是奇数，排除 AC，然后再代入其他选项。

3.2.2 倍数

C，7x 也必须是 3 的倍数。

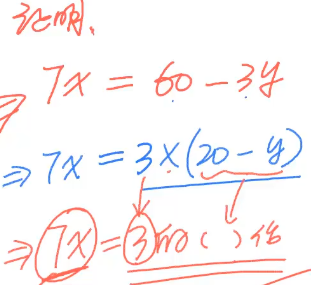
3.2.3 尾数

C，7x 的尾数只能是 1。

C

A

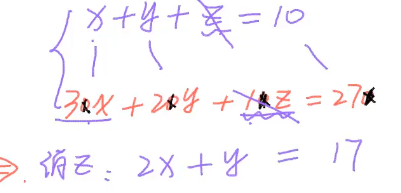
C，问最多有多少位选手获得一等奖，因此代入从大往小代入。

这篇关于行测-数量关系：1. 代入排除法、倍数特性法、方程法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---