多层感知机实现XOR门

单层感知机无法实现XOR门（即，无法求解非线性问题），这个也不是什么大问题，其实可以通过“叠加层”来表示，先不管叠加层的物理意义是什么，实现了再说！

XOR门通过NAND，AND，OR配置就能实现。

先看下面一张表，前三个门都实现了的。那么如何组合三个基础门实现XOR？

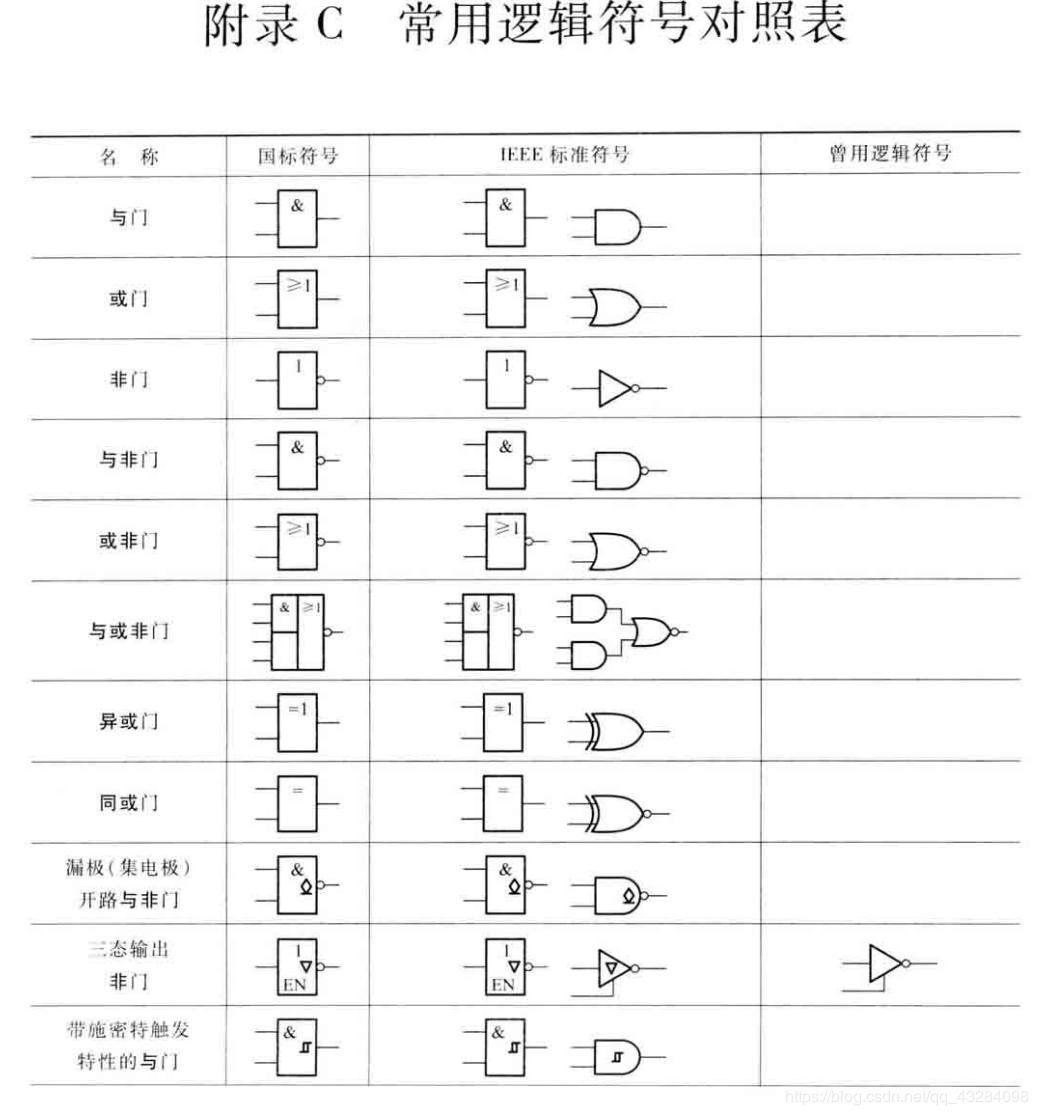
 XOR门可以通过下面这种配置来（NAND+OR+AND）实现。A和B表输入信号，Y表示输出。

 XOR门的真值表，对应上图，替换A，替换B，是NAND门的输出，是OR门的输出。

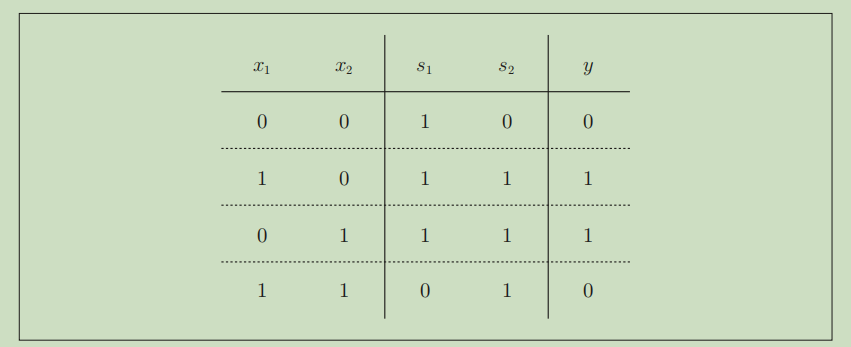
 现在用py实现下：

import numpy as np
def XOR(x1,x2):s1=NAND(x1,x2)s2=OR(x1,x2)y=AND(s1,s2)return ydef AND(x1,x2):x=np.array([x1,x2])   #inputw=np.array([0.5,0.5]) #set weightb=-0.7                #set offsettmp=np.sum(w*x)+bif tmp<=0:return 0else:return 1def NAND(x1,x2):x=np.array([x1,x2])   #inputw=np.array([-0.5,-0.5]) #set weightb=0.7                #set offsettmp=np.sum(w*x)+bif tmp<=0:return 0else:return 1
def OR(x1,x2):x=np.array([x1,x2])   #inputw=np.array([0.5,0.5]) #set weightb=-0.2                #set offsettmp=np.sum(w*x)+bif tmp<=0:return 0else:return 1print(XOR(0,0))
print(XOR(1,0))
print(XOR(0,1))
print(XOR(1,1))

 打印出来结果：

 以上貌似跟感知机没有啥关系，都是逻辑电路的思想，其实多层感知机就是一种多层结构的神经网络。换一种表达方式：

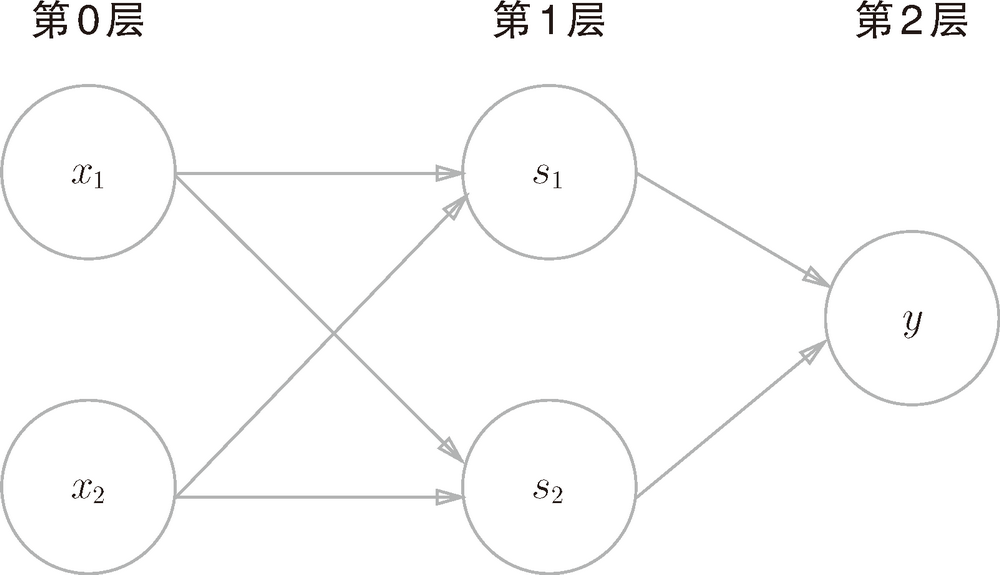
看上图，XOR门为多层结构的神经网络（这里就是多层感知机 multi-layered perceptron），0层、1层、2层都是划分好的，那么到底叫它几层感知机呢？严格意义上讲，权重的设置只存在于0-1层之间和1-2层之间，应该叫做2层感知机。不过有些paper把它认为是3层感知机，这里不纠结这个问题了。

XOR门的感知机的实现可以解释为：单层感知机无法表示的东西，通过增加层数来实现。反过来讲，通过叠加层，感知机能够表达更多更有意义的事情，例如：加法运算，进制转换,......。

其实，目前主流的计算机系统都可以用感知机表示。因为，主流计算机系统都是建立在Input-Porcess-Output (IPO)模式上的，那么问题来了，要什么样构造的感知机才能够表示计算机系统，多深才可以构建？

理论上，仅仅是理论上，2层就能构建。很多paper都说了，2层感知机，使用非线性的sigmoid函数激活，可以表示任意函数。但是弊端是，很难找到一个合适的权重。

所以，一般的思路还是按照：门电路-->半加器-->全加器-->ALU-->CPU，这一逻辑去构造计算机系统比较理性一点。