9_机械臂运动学_正解C++推导验证

1.前置知识

1.1  D-H矩阵表达式(改进型)

相邻连杆间坐标系变换通式：

R = Rot  T = Trans

i-1iT = Rx(αi-1)Tx(ai-1)Rz(θi)Tz(di)                         (9-1)

i-1iT = Screwx(ai-1, αi-1 )Screwz(di, θi)

ScrewQ(r, φ)代表沿Q轴平移r，再绕Q轴旋转角度φ的组合变换。由矩阵连乘计算表达式(9-1)得i-1iT的一般表达式为：

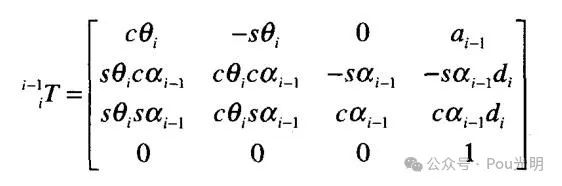
1.2 连续的连杆变换

如果已经定义了连杆坐标系和相应的连杆参数，就可以直接建立运动学方程。分别计算出各个连杆变换矩阵就能得出各个连杆参数的值。把这些连杆变换矩阵连乘就能得到一个坐标系{N}相对于坐标系{0}的变换矩阵：

0NT = 01T12T23T...N-1NT

变换矩阵0NT是关于n个关节变量的函数。如果能得到机器人各个关节位置传感器的值，机器人末端连杆在笛卡尔坐标系里的位置和姿态就能通过0NT计算出来。

1.3 使用C++ Eigen库验证遨博机械臂

/* D-H参数表 */    
double a[6] = {0.0, 0.0, 408.0, 376.0, 0.0, 0.0};
double al[6] = {0.0, -M_PI/2, M_PI, M_PI, -M_PI/2, M_PI/2};
double d[6] = {98.50, 121.50, 0.0, 0.0, 102.50, 94.0};
//各关节角度,单位弧度double th[6] = {0.0, 0.0, 0.0, 0.0,0.0, 0.0,};cos(th[i]),            -sin(th[i]),               0.0,          a[i],
sin(th[i])*cos(al[i]),  cos(th[i])*cos(al[i]),  -sin(al[i]),  -sin(al[i])*d[i],
sin(th[i])*sin(al[i]),  cos(th[i])*sin(al[i]),   cos(al[i]),   cos(al[i])*d[i],
0.0,  0.0,   0.0,   1.0;

for(int i=0; i<6; i++){
Eigen::Matrix4d tmp;
tmp <<  cos(th[i]),         -sin(th[i]),             0.0,           a[i],sin(th[i])*cos(al[i]),  cos(th[i])*cos(al[i]),  -sin(al[i]),  -sin(al[i])*d[i],sin(th[i])*sin(al[i]),  cos(th[i])*sin(al[i]),   cos(al[i]),  cos(al[i])*d[i],0.0,  0.0,   0.0, 1.0;T = tmp;if(0 == i) T06 = tmp;elseT06 = LastT*T;LastT = T06;}

程序结果：

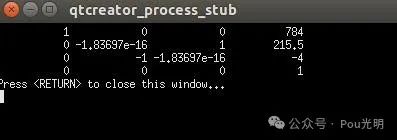
显然和遨博机械臂对不上，不过这个数值和之前matlab仿真的结果是一致的。所以需要加上offset调整一下。

 double offset[6] = {M_PI, -M_PI/2, 0.0, -M_PI/2, 0.0, 0.0};

double th[6] = {offset[0], offset[1], 0.0, offset[3], 0.0, 0.0};    

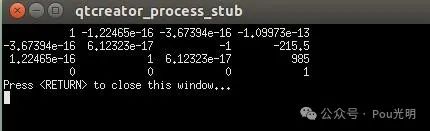
验证角度为30度，并打印姿态：

double th[6] = {M_PI/6+offset[0], M_PI/6+offset[1], M_PI/6, M_PI/6+offset[3], M_PI/6, M_PI/6};

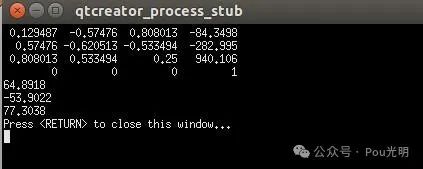
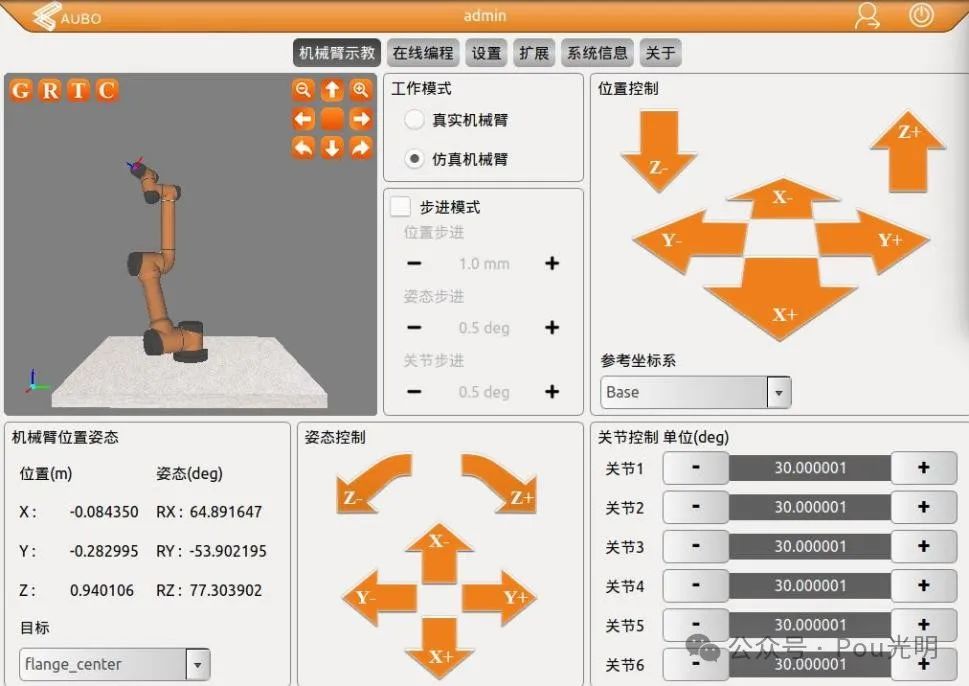
 结果是正确的。

 预计年前还有3篇笔记用来记录机械臂运动学6~8之间的学习记录。大概分别是刚体的转动、刚体空间转动的其他表示、齐次变换与D-H矩阵。   

      需要完整C++验证程序可在公众号后台留言：机械臂C++正解验证。 

机械臂其他相关笔记：

机械臂运动学正解验证

Matlab机械臂运动学示教演示

机械臂运动学D-H参数学习笔记(2)

3_机械臂运动学之刚体的运动

4_机械臂运动学基础向量空间

5_机械臂运动学基础_矩阵