本文主要是介绍python 基础知识点（蓝桥杯python科目个人复习计划27），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
今日复习内容：基础算法中的递归
1.介绍
- 递归：通过自我调用来解决问题的函数
- 递归通常把一个复杂的大问题层层转化为一个与原问题相似的规模较小的问题来解决
- 递归要注意：（1）递归出口；（2）当前问题如何变成子问题。
- 举个例子：
题目：写一个函数，求n的阶乘。
def f(n):# 递归出口if n <= 1:return 1ans = n * f(n - 1)return ans
print(f(5))运行结果：
我来解释一下这几行代码的计算过程：
输入5后，开始调用函数；
5 > 1，则f(5)= 5 * f(4) ;
4 > 1 , 则f(4)= 4 * f(3) ;
3 > 1 , 则f(3)= 3 * f(2) ;
2 > 1 , 则f(2)= 2 * f(1) ;
1 = 1 , 则f(1)= 1 ;
最终结果为：f(5) = 5 * 4 * 3 * 2 * 1 = 120
ok，具体计算过程就是这样。
2.汉诺塔问题
（我不会做动画，只能通过文字描述，我尝试过用word作图，但效果没那么好，所有就不粘贴图了）
大家应该都玩过这个游戏，有n个不同大小的圆盘和三根木柱（记为a,b,c），开始时，这些圆盘由大到小依次套到木柱a上，我们要做的就是把a上的圆盘通过b全部转移到c上，而且顺序也是从小到大。
游戏规则：（1）一次只能移动一个圆盘；（2）圆盘只能在3个木柱上存放；（3）在移动过程中，不允许大盘压小盘。
当n = 1时，只有一个盘子，移动一次就可以把a木柱上是所有盘中全部移动到c木柱上；
当n = 2时，以b木柱为中间桥梁，此时a木柱上有两个木柱（记为1，2），先把圆盘1移动到b木柱上，再把圆盘2移动到木柱c上，最后，再把圆盘1移动到木柱c上就ok了。所有，需移动3次。
......
具体操作步骤就是这样。
- 我把它转化成题的形式
定义函数Move，有n个盘子 ，3个木柱（记为A,B,C），圆盘从A移动到C，中间需借助B来完成。
即Move(n, A, B, C)；
考虑n个盘子的时候，将上面的（n - 1）个盘子视为一个整体：
（1）首先将（n - 1）个盘子从A移动到B，通过C，这就又变成了一个递归问题，即
Move(n - 1, A, C, B)；
（2）然后将A上剩下的那个圆盘移动到C，即A --> C；
（3）最后将（n - 1）个圆盘从B移动到C，通过A，又是一个递归函数，即Move(n - 1, B , C , A)；
（4）n = 0时，就是递归出口。
变成代码就是：
def Move(n,A,B,C):# 递归出口if n == 0:return# n - 1个盘子从A移动到B，通过CMove(n-1,A,C,B)# 第n个盘子从A移动到Cprint('{} --> {}'.format(A,C))# n-1个盘子从B移动到CMove(n-1,B,A,C)Move(3,'A','B','C')当n = 3时，运行结果为：
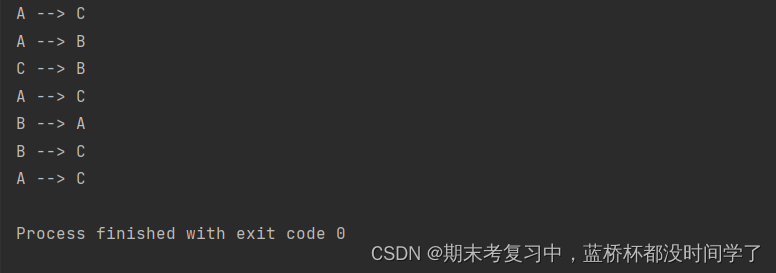这个思想就是把一个问题转化为n个子问题。
例题：
题目描述：
我们要求找出具有下列性质的数的个数（包括输入的自然数n）
先输入一个自然数n（n <= 1000),然后对此自然数按照如下方法进行处理：
1.不作任何处理；
2.在它的左边加上一个自然数，但该自然数不能超过该数的一半；
3.加上自然数后，继续按此规则进行处理，直到不能再加自然数为止。
思路：
将该问题分解成若干个子问题，上述操作等价于f(n)分解成所有f(i)方案之和，i <= n//2。
参考答案：
def f(n):if n == 1:return 1ans = 1for i in range(1,n //2 + 1):ans += f(i)return ans
n = int(input())
print(f(n))运行结果：
其中快速排序和归并排序也是递归的典型例子，可以结合着看。
若有疑问，可以提出。
OK，这篇就写到这里 ，下次继续！
这篇关于python 基础知识点（蓝桥杯python科目个人复习计划27）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
