本文主要是介绍python 基础知识点(蓝桥杯python科目个人复习计划26),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
今日复习内容:基础算法中的前缀和
1.定义:
- 前缀和:对于一个长度为n的列表a,前缀和为: sum[i] = a[1] + ...+a[i];
- 例如:a = [1,2,3,4,5],则它的前缀和数组sum为:[1,3,6,10,15]。
2.前缀和的性质
- sum[i] = sum[i-1] + a[i]
- a[l] + ... + a[r] = sum[i] - sum[l-1]
- 第一条性质用于处理前缀和
- 第二条性质可以在O(1)的时间内求出区间和
将其转化为代码得:
第一种方式:
# 求出a的前缀和
def get_presum(a):n = len(a)sum = [0] * nsum[0] = a[0]for i in range(1,n):sum[i] = sum[i-1] + a[i]return sum
# 求区间a[i]...a[r]之和
def get_sum(sum,l,r):if 1 == 0:return sum[r]else:return sum[r] - sum[l - 1]a = [1,2,3,4,5]
sum = get_presum(a)
print('a = ',a)
print('sum = ',sum)
print(get_sum(sum,2,3))运行结果:
第二种方式:
from itertools import accumulate
# 求出a的前缀和
def get_presum(a):sum = list(accumulate(a))return sum
# 求区间a[i]...a[r]之和
def get_sum(sum,l,r):if l == 0:return sum[r]else:return sum[r] - sum[l-1]a = [1,2,3,4,5]
sum = get_presum(a)
print('a = ',a)
print('sum = ',sum)
print(get_sum(sum,2,3))运行结果:

3.习题
例题1:区间次方和
题目描述:
给定一个长度为n的整数数组a以及m个查询。
每个查询包括三个整数l,r,k表示询问l至r之间所有元素的k次方和。
请对每个查询输出一个答案,答案对10^9 + 7 取模。
输入格式:
第一行输入两个整数n和m,其含义如上所述。
第二行输入n个整数a[1],a[2],...a[n];
接下来m行,每行输入三个整数l,r,k表示一个查询。
输出格式:
输出m行,每行一个整数,表示查询的答案对10^9 + 7 取模的结果。
(k <= 5,对于每个k可以利用前缀和求解)
参考答案:
from itertools import accumulate
MOD = 1000000007
# 求出a的前缀和
def get_presum(a):sum = list(accumulate(a))sum = [x % MOD for x in sum]return sum
# 求区间a[i]...a[r]之和
def get_sum(sum,l,r):if l == 0:return sum[r]else:return (sum[r] - sum[l-1] + MOD) % MODn,m = map(int,input().split())
a = list(map(int,input().split()))# 存储a数组的前缀和,a数组平方的前缀和......
sum_list = []
for i in range(1,6):tem_a = [x ** i for x in a]sum_list.append(get_presum(tem_a))for _ in range(m):l,r,k = map(int,input().split())print(get_sum(sum_list[k - 1],l - 1,r - 1))
运行结果:

这个题本身不难,需搞懂我前面所提到的知识点。
例题2:小郑的蓝桥平衡串
题目描述:
平衡串指的是字符串,其中包含两种不同字符,并且这两种字符的数量相等;
例如:ababab 和aababb都是平衡字符串,因为每种字符各有三个,而abaab和aaaab都不是平衡字符串,因为每种字符串的数量并不相等;
平衡串在密码学和计算机科学中有重要应用,比如可以用来构造哈希函数或者解决一些数学问题。
小郑拿到一个仅含义L和Q的字符串,他的任务就是找到最长平衡串,且满足平衡串的要求,即保证子串中L和Q数量的相等。
输入格式:
输入一行字符串,保证字符串中只有L和Q。
输出格式:
输出一个整数,为输入字符串中最长平衡串的长度。
思路:
可以将L和Q转换成数字,例如L为+1,Q为-1,问题就变为求区间和为0的最长区间,再枚举所有的区间即可。
参考答案:
from itertools import accumulate
MOD = 1000000007
# 求出a的前缀和
def get_presum(a):sum = list(accumulate(a))sum = [x % MOD for x in sum]return sum
# 求区间a[i]...a[r]之和
def get_sum(sum,l,r):if l == 0:return sum[r]else:return (sum[r] - sum[l-1] + MOD) % MOD
S = input()
n = len(S)
a = []
for x in S:if x == 'L':a.append(1)else:a.append(-1)
sum = get_presum(a)
ans = 0
for l in range(n):for r in range(l,n):if get_sum(sum,l,r) == 0:ans = max(ans,r - l + 1)
print(ans)运行结果:

4.二维前缀和
(1) 定义:
前缀和:对于N*M的二维列表a(下标统一从1开始),前缀和为:
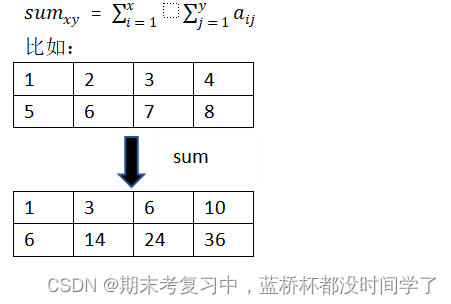
(2)公式
- 下标从1,1开始,有如下统一公式:

这个公式的证明过程和《概率论与数理统计》中“概率求和公式的推导” 是一样的。
- 举个例子

把它转化成代码,如下:
def output(a,n):for i in range(1,n+1):print(' '.join(map(str,a[i][1:])))
n,m = map(int,input().split())
# 下标从1开始
a = [[0] * (m + 1) for i in range(n + 1)]
sum = [[0] * (m + 1) for i in range(n + 1)]
# 输入一个二维数组
for i in range(1,n + 1):a[i] = [0] + list(map(int,input().split()))
output(a,n)for i in range(1,n + 1):for j in range(1,m + 1):sum[i][j] = sum[i-1][j] + sum[i][j-1] + a[i][j] - sum[i-1][j-1]
output(sum,n)运行结果:

增加点难度 :

(3)习题
例题1:统计子矩阵
题目描述:
给定一个N*M的矩阵A,请你统计有多少个子矩阵(最小为1*1的,最大为N*M的)满足子矩阵中所有数的和不超过给定的整数K?
输入格式:
第一行包含三个整数N,M,K;
之后N行每行包括M个整数,代表矩阵A。
输出格式:
一个整数代表答案。
对于30%的数据,N,M <= 20;
对于70%的数据,N,M <= 100;
对于100%的数据,1 <= N,M <= 500;0 <= A(ij) <= 1000;1 <= K <= 250000000。
思路:
枚举所有的子矩阵,然后利用二维前缀和求解矩阵中元素之和。
参考答案:
n, m, k = map(int,input().split())
# 下标从1开始
a = [[0] * (m + 1) for i in range(n + 1)]
sum = [[0] * (m + 1) for i in range(n + 1)]# 输入一个二维数组
for i in range(1,n + 1):a[i] = [0] + list(map(int,input().split()))# 求二维前缀和
for i in range(1,n + 1):for j in range(1,m + 1):sum[i][j] = sum[i-1][j] + sum[i][j-1] - sum[i-1][j-1] + a[i][j]def get_sum(sum,x1,y1,x2,y2):return sum[x2][y2] -sum[x1-1][y2] -sum[x2][y1-1] +sum[x1-1][y1-1]ans = 0
# 枚举左上角
for x1 in range(1,n + 1):for y1 in range(1,m + 1):# 枚举右上角for x2 in range(x1,n + 1):for y2 in range(y1,m + 1):if get_sum(sum,x1,y1,x2,y2) <= k:ans += 1
print(ans)运行结果:
OK,今天就写到这里了,这个题我做了50分钟左右,心累啊。
若有疑问,可以提出,一起交流。
下次继续!
这篇关于python 基础知识点(蓝桥杯python科目个人复习计划26)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







