本文主要是介绍直线拟合(支持任意维空间的直线拟合,附代码),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 一、问题描述
- 二、推导步骤
- 三、 M A T L A B MATLAB MATLAB代码
一、问题描述
给定一系列的三维空间点 ( x i , y i , z i ) , i = 1 , 2 , . . . , n (x_i,y_i,z_i),i=1,2,...,n (xi,yi,zi),i=1,2,...,n,拟合得到直线的方程。本文的直线拟合方法适用于任意维空间的直线拟合,不失一般性,这里以三维空间的直线拟合为例。本文的直线拟合方法的基本思想参考博文:最小二乘法三维(k维)直线拟合。
二、推导步骤
设直线的点向式方程为:
x − x 0 a = y − y 0 b = z − z 0 c = s (1) \frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}=s \tag 1 ax−x0=by−y0=cz−z0=s(1)
由式(1),得到直线的参数方程为:
{ x = x 0 + a s y = y 0 + b s z = z 0 + c s (2) \left\{ \begin{array}{c} x=x_0+as \\ y=y_0+bs \\ \tag 2 z=z_0+cs\end{array}\right. ⎩ ⎨ ⎧x=x0+asy=y0+bsz=z0+cs(2)
式(2)写成向量形式为:
L = L 0 + v s (3) \bm{L}=\bm{L_0}+\bm{v}s \tag 3 L=L0+vs(3)
其中, L = [ x , y , z ] T \bm{L}=[x,y,z]^T L=[x,y,z]T, L 0 = [ x 0 , y 0 , z 0 ] T \bm{L_0}=[x_0,y_0,z_0]^T L0=[x0,y0,z0]T为直线上任意一点, v = [ a , b , c ] T \bm{v}=[a,b,c]^T v=[a,b,c]T为直线的单位方向向量。
如下图,红色点 L i ( x i , y i , z i ) L_i(x_i,y_i,z_i) Li(xi,yi,zi)为给定的一系列三维空间点,根据给定三维空间点,拟合直线方程(3),也就是计算 L 0 \bm{L_0} L0和 v \bm{v} v,使得在某种“距离”的度量下,达到最佳的直线拟合效果。
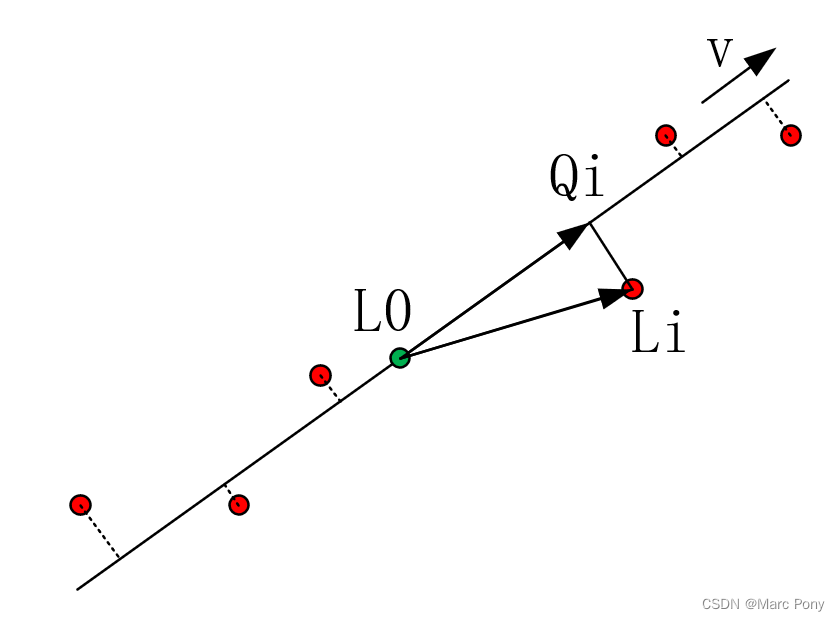
点 L i L_i Li到直线距离的平方为:
∣ ∣ Q i L i ∣ ∣ 2 = ∣ ∣ L 0 L i ∣ ∣ 2 − ∣ ∣ L 0 Q i ∣ ∣ 2 (4) ||\bm{Q_iL_i}||^2 = ||\bm{L_0L_i}||^2 -||\bm{L_0Q_i}||^2 \tag 4 ∣∣QiLi∣∣2=∣∣L0Li∣∣2−∣∣L0Qi∣∣2(4)
L 0 L i \bm{L_0L_i} L0Li在直线的投影的平方为:
∣ ∣ L 0 Q i ∣ ∣ 2 = ( L 0 L i ⋅ v ) 2 (5) ||\bm{L_0Q_i}||^2= (\bm{L_0L_i} \cdot \bm{v})^2\tag 5 ∣∣L0Qi∣∣2=(L0Li⋅v)2(5)
令向量 Y i = L 0 L i = L i − L 0 \bm{Y_i}=\bm{L_0L_i}=\bm{L_i}-\bm{L_0} Yi=L0Li=Li−L0,式(4)写成:
∣ ∣ Q i L i ∣ ∣ 2 = ∣ ∣ Y i ∣ ∣ 2 − ( Y i ⋅ v ) 2 = Y i T Y i − ( v T Y i ) 2 (6) ||\bm{Q_iL_i}||^2 = ||\bm{Y_i}||^2 -(\bm{Y_i} \cdot \bm{v})^2= \bm{Y_i}^T \bm{Y_i} -(\bm{v}^T \bm{Y_i})^2 \tag 6 ∣∣QiLi∣∣2=∣∣Yi∣∣2−(Yi⋅v)2=YiTYi−(vTYi)2(6)
在最小二乘准则下,可以建立直线拟合的优化模型目标函数:
f = ∑ i = 1 n ∣ ∣ Q i L i ∣ ∣ 2 = ∑ i = 1 n [ Y i T Y i − ( v T Y i ) 2 ] (7) f=\sum\limits_{i=1}^{n} ||\bm{Q_iL_i}||^2 = \sum\limits_{i=1}^{n}[ \bm{Y_i}^T \bm{Y_i} -(\bm{v}^T \bm{Y_i})^2] \tag 7 f=i=1∑n∣∣QiLi∣∣2=i=1∑n[YiTYi−(vTYi)2](7)
计算 L 0 \bm{L_0} L0:
目标函数 f f f对向量 Y i \bm{Y_i} Yi求偏导数:
∂ f ∂ Y i = ∑ i = 1 n ( 2 Y i − 2 v T Y i v ) = ∑ i = 1 n ( 2 Y i − 2 v v T Y i ) = ∑ i = 1 n 2 ( I − v v T ) Y i (8) \frac{ \partial f }{ \partial \bm{Y_i} }=\sum\limits_{i=1}^{n} ( 2\bm{Y_i} -2\bm{v}^T \bm{Y_i}\bm{v})=\sum\limits_{i=1}^{n} ( 2\bm{Y_i} -2\bm{v}\bm{v}^T \bm{Y_i})=\sum\limits_{i=1}^{n}2 (\bm{ I} -\bm{v}\bm{v}^T ) \bm{Y_i}\tag 8 ∂Yi∂f=i=1∑n(2Yi−2vTYiv)=i=1∑n(2Yi−2vvTYi)=i=1∑n2(I−vvT)Yi(8)
式(8)中,利用了恒等式 v T Y i v ≡ v v T Y i \bm{v}^T \bm{Y_i}\bm{v}\equiv \bm{v}\bm{v}^T \bm{Y_i} vTYiv≡vvTYi,简单进行验算可以证明该恒等式。
由于 v \bm{v} v为单位向量,可以证明 I − v v T ≠ 0 \bm{ I} -\bm{v}\bm{v}^T\ne \bm{0} I−vvT=0。
因此
∑ i = 1 n Y i = ∑ i = 1 n ( L i − L 0 ) = ∑ i = 1 n L i − n L 0 = 0 (9) \sum\limits_{i=1}^{n}\bm{Y_i}= \sum\limits_{i=1}^{n}(\bm{L_i}-\bm{L_0})=\sum\limits_{i=1}^{n}\bm{L_i}-n\bm{L_0}=\bm{0}\tag 9 i=1∑nYi=i=1∑n(Li−L0)=i=1∑nLi−nL0=0(9)
L 0 = 1 n ∑ i = 1 n L i (10) \bm{L_0}=\frac{1}{n}\sum\limits_{i=1}^{n}\bm{L_i}\tag {10} L0=n1i=1∑nLi(10)
可以得到结论:待拟合的直线经过一个点 L 0 \bm{L_0} L0,该点的坐标为所有给定点的坐标平均值。如下图所示,一旦确定直线的单位方向向量 v \bm{v} v,则直线的方程便确定。
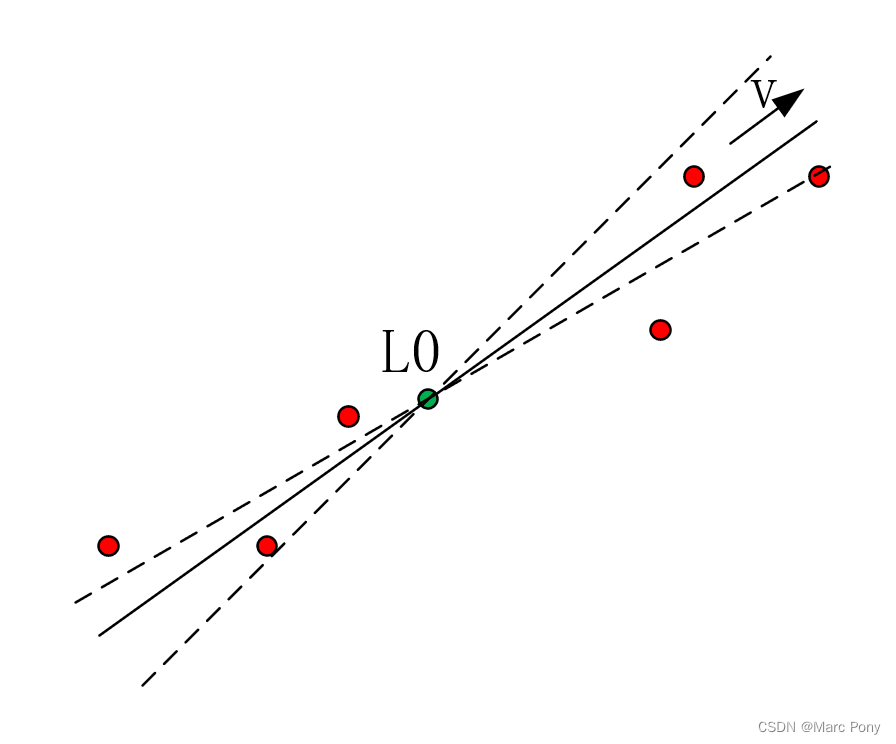
计算 v \bm{v} v:
对于单位向量 v \bm{v} v, v T v = 1 \bm{v}^T\bm{v}=1 vTv=1,可以证明: Y i T Y i ≡ v T ( Y i T Y i ) v \bm{Y_i}^T \bm{Y_i} \equiv\bm{v^T}(\bm{Y_i}^T \bm{Y_i})\bm{v} YiTYi≡vT(YiTYi)v, ( v T Y i ) 2 ≡ v T ( Y i Y i T ) v (\bm{v}^T \bm{Y_i})^2 \equiv \bm{v}^T(\bm{Y_i}\bm{Y_i^T})\bm{v} (vTYi)2≡vT(YiYiT)v
式(7)可改写成:
f = ∑ i = 1 n [ Y i T Y i − ( v T Y i ) 2 ] = ∑ i = 1 n [ v T ( Y i T Y i ) v − v T ( Y i Y i T ) v ] = v T ∑ i = 1 n [ ( Y i T Y i ) I − Y i Y i T ] v (11) f=\sum\limits_{i=1}^{n}[ \bm{Y_i}^T \bm{Y_i} -(\bm{v}^T \bm{Y_i})^2] =\sum\limits_{i=1}^{n}[ \bm{v^T}(\bm{Y_i}^T \bm{Y_i})\bm{v} -\bm{v}^T(\bm{Y_i}\bm{Y_i^T})\bm{v}] = \bm{v^T}\sum\limits_{i=1}^{n}[ (\bm{Y_i}^T \bm{Y_i}) \bm{I} -\bm{Y_i}\bm{Y_i^T}] \bm{v}\tag {11} f=i=1∑n[YiTYi−(vTYi)2]=i=1∑n[vT(YiTYi)v−vT(YiYiT)v]=vTi=1∑n[(YiTYi)I−YiYiT]v(11)
令矩阵 S = ∑ i = 1 n [ ( Y i T Y i ) I − Y i Y i T ] S=\sum\limits_{i=1}^{n}[ (\bm{Y_i}^T \bm{Y_i}) \bm{I} -\bm{Y_i}\bm{Y_i^T}] S=i=1∑n[(YiTYi)I−YiYiT],式(11)可写成:
f = v T S v (12) f= \bm{v^T}S \bm{v}\tag {12} f=vTSv(12)
f f f的最小值为矩阵 S S S最小特征值对应的特征向量。直线方向向量 v v v的求解问题转化为矩阵最小特征值对应的特征向量的求解问题!
三、 M A T L A B MATLAB MATLAB代码
%{
Function: line_fitting
Description: 直线拟合
Input: 任意维直线点数据points,行数为点个数,列数为点的维数
Output: 拟合得到的直线经过的一点L0,直线的单位方向向量v
Author: Marc Pony(marc_pony@163.com)
%}
function [L0, v] = line_fitting(points)
n = size(points, 1);
x = points(:, 1);
y = points(:, 2);
z = points(:, 3);L0 = [mean(x); mean(y); mean(z)];
S = zeros(3,3);
for i = 1 : nYi = [x(i) - L0(1); y(i) - L0(2); z(i) - L0(3)];S = S + (Yi' * Yi * eye(3, 3) - Yi * Yi');
end
[V, ~] = eig(S);v = V(:, 1); %矩阵S最小特征值对应的特征向量
end
%{
Function: generate_line_points
Description: 直线路径点生成
Input: 直线经过的一点L0,直线的单位方向向量v,点个数n,路径标量最小值minS,路径标量最大值maxS
Output: 任意维直线点数据points,行数为点个数,列数为点的维数
Author: Marc Pony(marc_pony@163.com)
%}
function points = generate_line_points(L0, v, n, minS, maxS)
points = zeros(n, length(v));
s = linspace(minS, maxS, n);
for i = 1 : npoints(i, :) = (L0 + v * s(i))';
end
end
clear
clc
close all%% 验证恒等式: v'*Yi*v = v*v'*Yi
syms v1 v2 v3 y1 y2 y3 real
v = [v1; v2; v3];
Yi = [y1; y2; y3];
res1 = simplify(v'*Yi*v - v*v'*Yi)%% 验证恒等式: Yi'*Yi = v'*(Yi'*Yi)*v, 其中v'*v=1
res2 = [Yi'*Yi; simplify(v'*(Yi'*Yi)*v)]%% 验证恒等式: (v'*Yi)^2 = v'*(Yi*Yi')*v
res3 = simplify((v'*Yi)^2 - v'*(Yi*Yi')*v)% points = [1 0 0
% 1 10 0
% 1 20 0
% ];
% points = [0 1 0
% 10 1 0
% 200 1 0
% ];
% points = [1 1 1
% 2 1 2
% ];figure
axis([-10, 10, -10, 10])
hold on
pointCount = 6;
points = zeros(pointCount, 3);
for i = 1 : pointCount[points(i, 1), points(i, 2)] = ginput(1);plot(points(i, 1), points(i, 2), '+')
end[L0, v] = line_fitting(points)n = 100;
len = sqrt((max(points(:,1)) - min(points(:,1)))^2 + (max(points(:,2)) - min(points(:,2)))^2 + (max(points(:,3)) - min(points(:,3)))^2);
minS = -0.6 * len;
maxS = 0.6 * len;
p = generate_line_points(L0, v, n, minS, maxS);
plot3(p(:,1), p(:,2), p(:,3), '-')
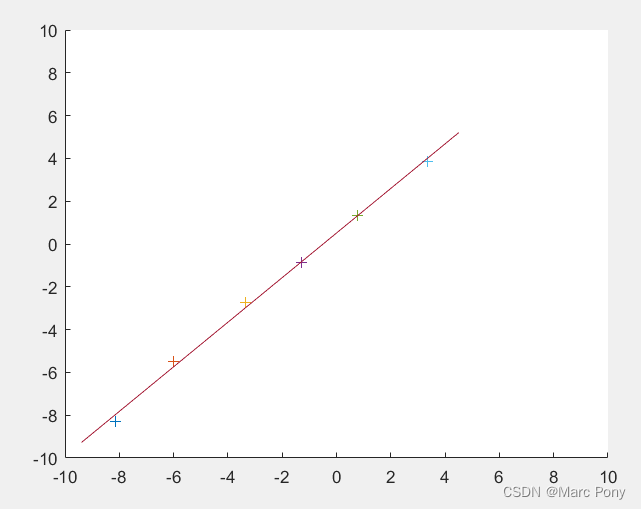
这篇关于直线拟合(支持任意维空间的直线拟合,附代码)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




