本文主要是介绍刷题总结 1.23，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
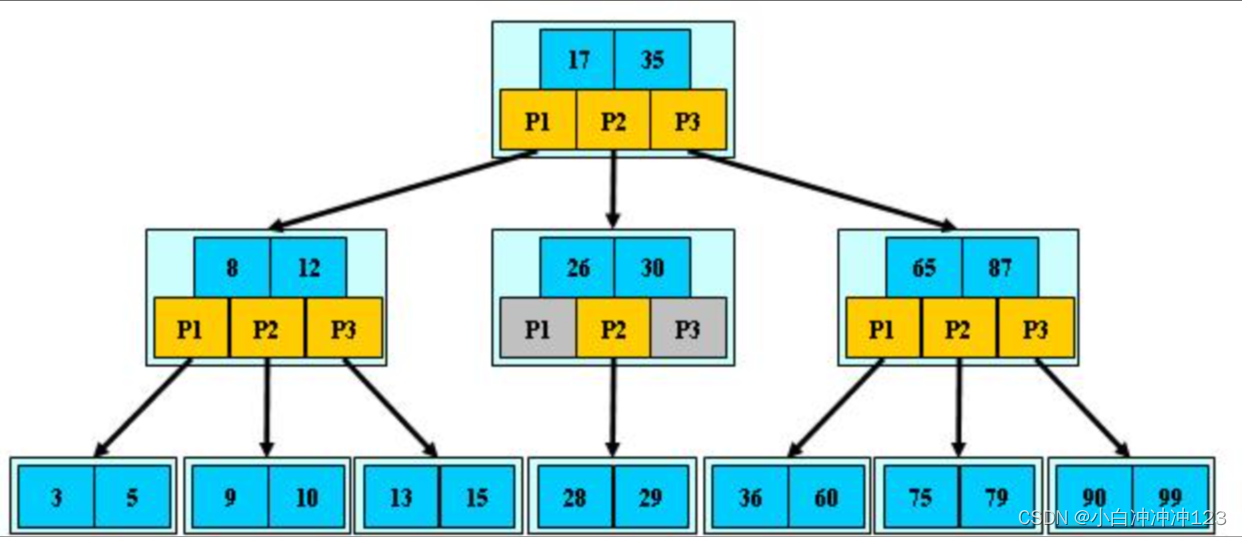
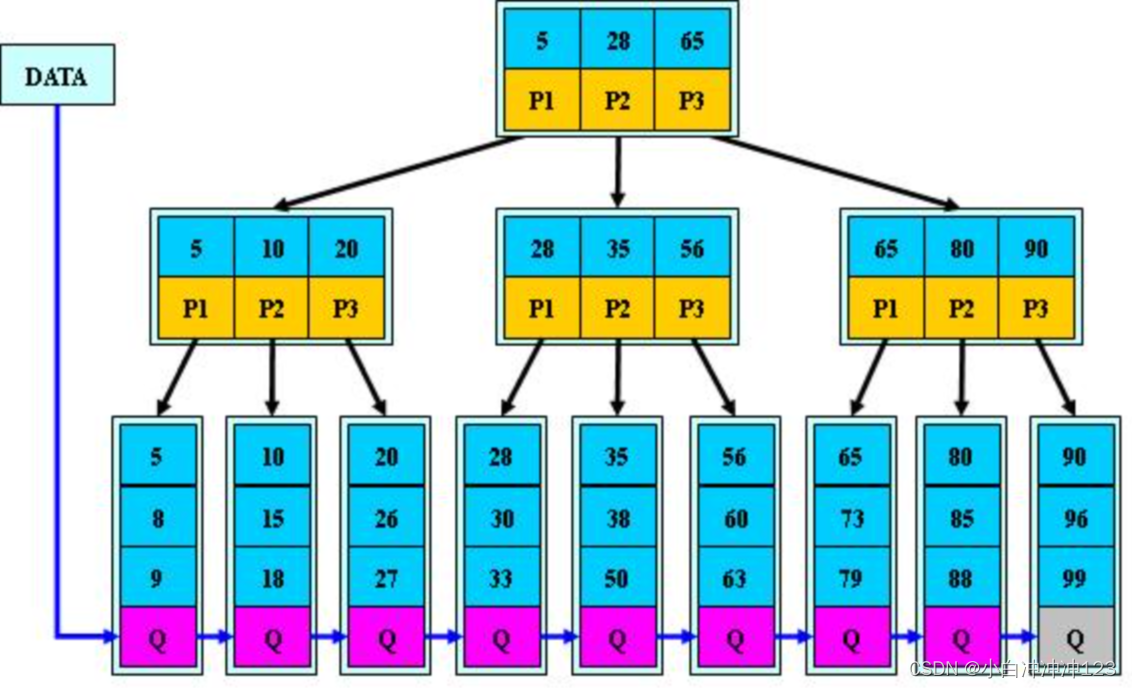
三阶B-树根节点最少有一个关键字，其他节点最少【3/2】-1（向上取整），即为1；
所以该B树为一颗满二叉树，关键字个数为31；
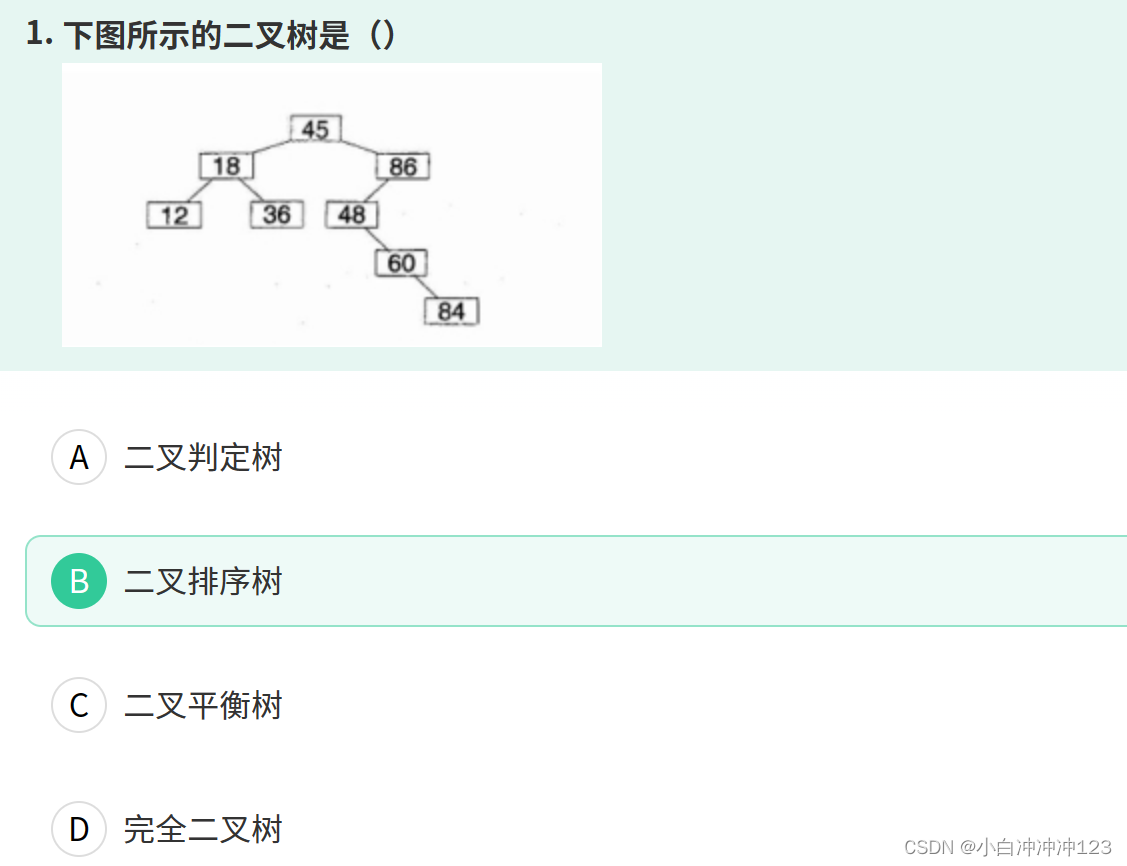
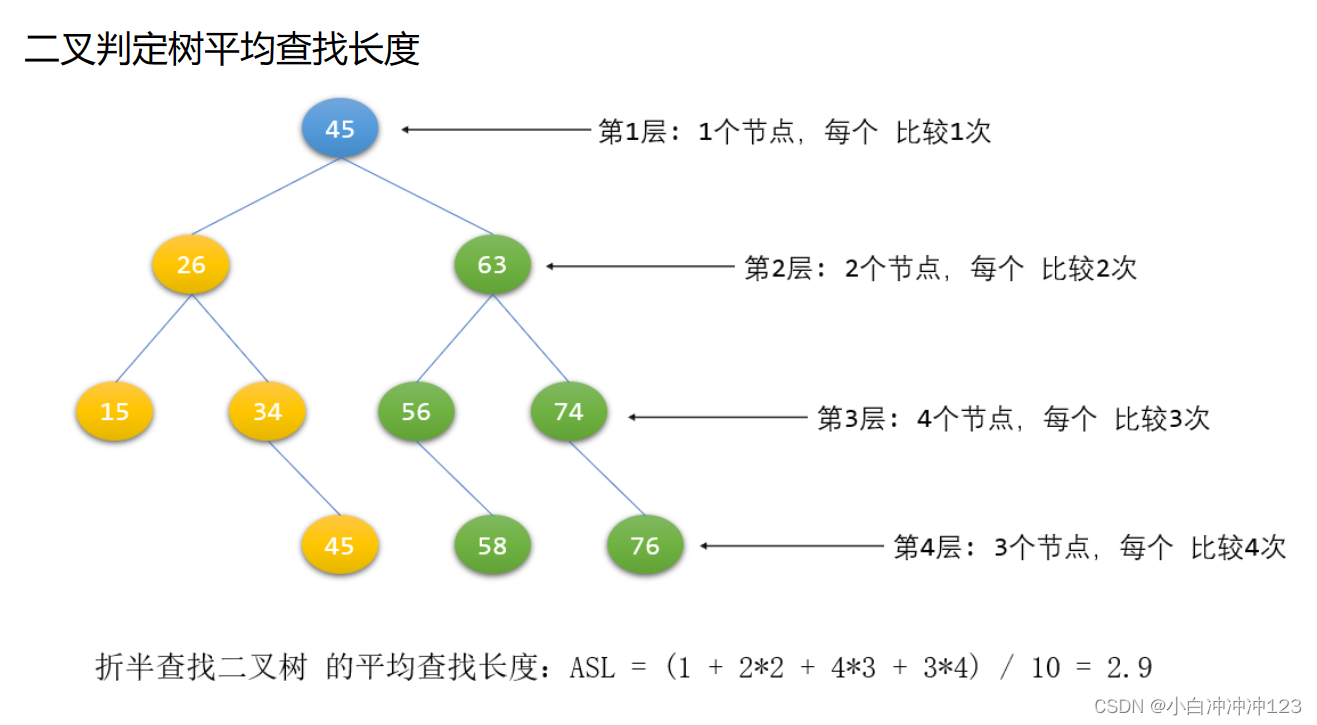
这里的最优二叉树指的是赫夫曼二叉树，由赫夫曼二叉树的构造可以知道：n个叶子结点的赫夫曼树总共有2n-1个结点，那么分支结点的个数=总结点数 - 叶子结点数 = 2n-1-n = n-1 。
最优二叉树中只有n0和n2，而二叉树的性质是n2=n0-1,所以n-1
只有根的顺序在变，左右子树一直都是先左后右，不分遍历
（^的优先级比 *高）
卡特兰公式：
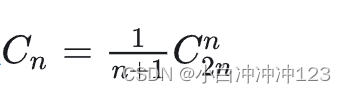
所以一共3个元素，一共有5种出栈方式，其中作为标识符的只有字母和下划线开头的，所以有
a_3，a3_，_3a，_a3这四种情况：但是_a3情况不可能实现，所以为3种。
从右至左扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（栈顶元素 op 次顶元素），并将结果入栈；重复上述过程直到表达式最左端，最后运算得出的值即为表达式的结果。
根据从右至左扫描计算过程如下:
题目中的前缀形式为：+-*^ABCD/E/F+GH
1) 首先扫描 H,是数字 入栈 ，栈中为: H
2) 扫描 G 为数字 入栈 ,栈中为:G,H
3)扫描+ 为运算符 ,依次弹出G ,H ,得到 G+H 的结果 入栈，栈中为： G+H(在这里方便讲解 标记为 G+H)
4)扫描 F 为数字 ,入栈 ，栈中为 F, G+H
5)扫描 / 为运算符, 依次弹出 F,G+H ，计算F/(G+H) 的结果入栈 ，栈中为 F/(G+H)
6)扫描 E 为数字,入栈，栈中为 E, F/(G+H)
7) 扫描 / 为运算符, 依次弹出E, F/(G+H) ，计算 E/(F/(G+H))
8)扫描 D 为数字,入栈 栈中为:D, E/(F/(G+H))
9) 扫描 C 为数字,入栈 栈中为:C,D, E/(F/(G+H))
10) 扫描 B 为数字,入栈 栈中为:B,C,D, E/(F/(G+H))
11) 扫描 A 为数字,入栈 栈中为:A,B,C,D, E/(F/(G+H))
12) 扫描^ 为数字,依次弹出 A,B 计算 A^B的结果入栈, 栈中为：A^B ,C,D, E/(F/(G+H))
13) 扫描*为数字,依次弹出 A^B,C 计算 A^B*C的结果入栈, 栈中为：A^B* C,D, E/(F/(G+H))
14) 扫描-为数字,依次弹出 A^B*C,D 计算 A^B*C-D的结果入栈, 栈中为：A^B* C-D, E/(F/(G+H))
15) 扫描+为数字,依次弹出 A^B*C-D, E/(F/(G+H)) 计算 A^B*C-D+ E/(F/(G+H)) 的到结果
最后得到的表达式为： A^B* C-D+ E/(F/(G+H))
栈和队列都是特殊的线性表，都有顺序存储和链式存储，顺序栈和链式栈
元素出栈顺序未知。除非 a1=n，则说明元素全部入栈之后再弹出，此时出栈顺序则为a(n),a(n-1)...a(1)。这样答案就是 B 了。
注意：要看清条件背后的本质，实际就是问n的出栈时间可以发生在任一时刻时，问n出栈后的大家的出栈顺序。而这是不确定的，除非n是第一个出栈，那就说明是在所有元素都进栈之后，再出栈，这时可以确定。
这篇关于刷题总结 1.23的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
