Matlab解决简单4次牛顿差值,Matlab插值法

实验目的：

1.Matlab中多项式的表示及多项式运算

2.用Matlab实现拉格朗日及牛顿插值法

3.用多项式插值法拟合数据

实验要求：

1.掌握多项式的表示和运算

2.拉格朗日插值法的实现(参见吕同富版教材)

3.牛顿插值法的实现(参见吕同富版教材)

实验内容：

1.多项式的表达式和创建；多项式的四则运算、导数与积分。

2.用Matlab实现拉格朗日及牛顿插值法。

3.用多项式插值法拟合数据。

实验步骤：

1.多项式的表达式，MATLAB中使用以为向量来表示多项式，将多项式的系数按照降幂次序存放在向量中。多项式P(x)的具体表示方法：

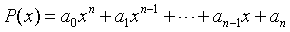的系数构成向量为：

。示例如下：

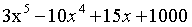
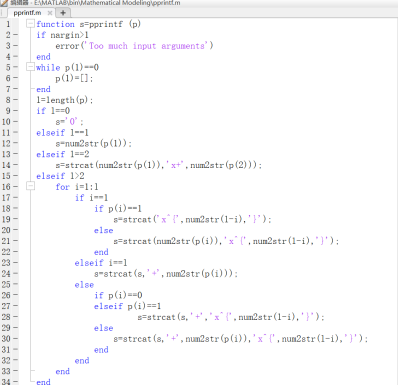
将向量表示的多项式用字符串输出的通用函数示例：

例子

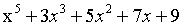运行示例：

多项式的加法：

结果是

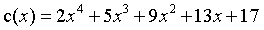
多项式乘法：

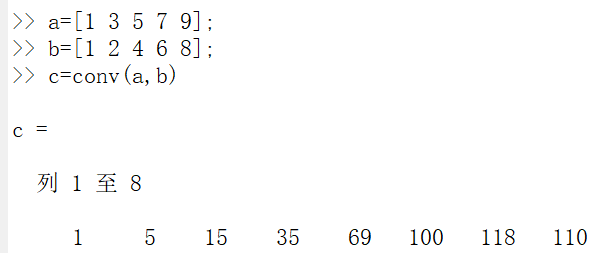
结果是

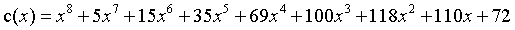
多项式除法：

多项式导数：

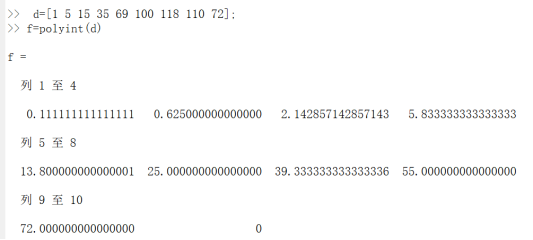
2.用Matlab实现拉格朗日，拉格朗日代码：

1 function yi=Lagrange(x,y,xi)

2 m=length(x);n=length(y);p=length(xi);

3 if m~=n

4 error('向量x与y的长度必须一致');

5 end

6 s=0;

7 for k=1:n

8 t=ones(1,p);

9 for j=1:n

10 if j~=k

11 t=t.*(xi-x(j))./(x(k)-x(j));

12 end

13 end

14 s=s+t.*y(k);

15 end

16 yi=s;

17 end

Lagrange

运行示例：

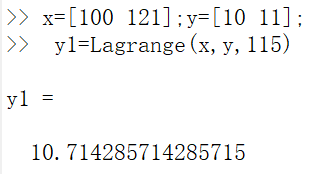
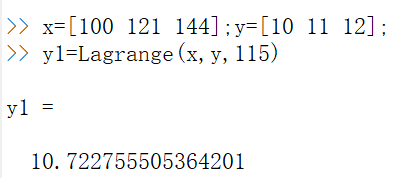
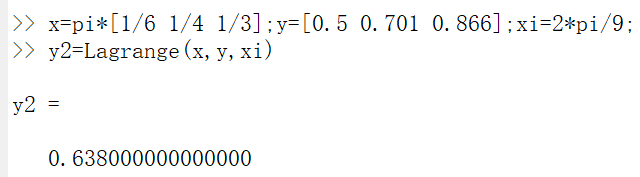
牛顿插值法代码：

1 function yi=newtonint(x,y,xi)

2 m=length(x);n=length(y);

3 if m~=n

4 error('向量x与y的长度必须一致');

5 end

6 A=zeros(n);

7 A(:,1)=y;

8 for j=2:n%j为列标

9 for i=1:(n-j+1) %i为行标

10 A(i,j)=(A(i+1,j-1)-A(i,j-1))/(x(i+j-1)-x(i));%计算差商表

11 end

12 end

13 %根据差商表,求对应的牛顿插值多项式在x=xi处的值yi

14 N(1)=A(1,1);

15 for j=2:n

16 T=1;

17 for i=1:j-1

18 T=T*(xi-x(i));

19 end

20 N(j)=A(1,j)*T;

21 end

22 yi=sum(N); %将x=xi带入牛顿插值多项式，得到的yi的值

23 %A 输出差商表

24 end

newtonint

运行实例：

等距节点的牛顿向后插值代码：

1 function yi=newtonint1(x,y,xi)

2 h=x(2)-x(1);t=(xi-x(1))/h;

3 n=length(y);Y=zeros(n);Y(:,1)=y';

4 for k=1:n-1

5 Y(:,k+1)=[diff(y',k);zeros(k,1)];

6 end

7 yi=Y(1,1);

8 for i=1:n-1

9 z=t;

10 for k=1:i-1

11 z=z*(t-k);

12 end

13 yi=yi+Y(1,i+1)*z/prod([1:i]);

14 end

newtonint1

运行实例：

等距节点的牛顿向前插值代码：

1 function yi=newtonint2(x,y,xi)

2 n=length(x);h=x(n)-x(n-1);t=(x(n)-xi)/h;

3 n=length(y);Y=zeros(n);Y(:,1)=y';

4 for k=1:n-1

5 Y(:,k+1)=[zeros(k,1);diff(y',k)];

6 end

7 h=x(n)-x(n-1);t=(x(n)-xi)/h;yi=Y(n,1);

8 for i=1:n-1

9 z=t;

10 for k=1:i-1

11 z=z*(t-k);

12 end

13 yi=yi+Y(n,i+1)*(-1)^i*z/prod([1:i]);

14 end

newtonint2

运行示例：

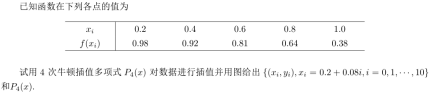
3.使用4次牛顿插值多项式插值，并作图：

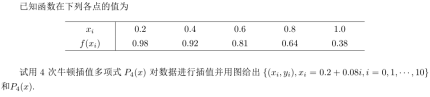
解：由4次牛顿插值多项式，

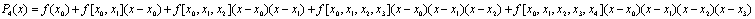
求上述多项式的系数：(修改newtonint.m代码，得到差商表)，代码如下：

1 function B=newtonint4(x,y)

2 m=length(x);n=length(y);

3 if m~=n

4 error('向量x与y的长度必须一致');

5 end

6 A=zeros(n);

7 A(:,1)=y;

8 for j=2:n%j为列标

9 for i=1:(n-j+1) %i为行标

10 A(i,j)=(A(i+1,j-1)-A(i,j-1))/(x(i+j-1)-x(i));%计算差商表

11 end

12 end

13 B=A;

14 end

newtonint4

代入数据得到差商表：

0.98

-0.3

-0.625

-0.2083

-0.5208

0.92

-0.55

-0.75

-0.625

0

0.81

-0.85

-1.125

0

0

0.64

-1.3

0

0

0

0.38

0

0

0

0

已知，第一行的便是插值多项式的系数，代入插值多项式：

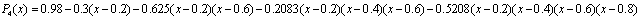
并作出图像：

1 x0=[0.2 0.4 0.6 0.8 1.0];

2 y0=[0.98 0.92 0.81 0.64 0.38];

3 plot(x0,y0,'b-o')

4 hold on

5 k=0:1:10;

6 x=0.2+0.08*k;

7 for i=1:1:11

8 y(i)=0.98-0.3*(x(i)-0.2)-0.625*(x(i)-0.2)*(x(i)-0.4)-0.2083333*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0.6)-0.520833333*(x(i)-0.2)*(x(i)-0.4)*(x(i)-0.6)*(x(i)-0.8);

9 end

10 plot(x,y,'r-o');

11 legend('原图像','4次插值图像');

plot3

小结：

在编写牛顿插值的代码时，我遇到了超出元组索引的问题。我在MATLAB的提示下(它的提示是英语)，如图：

这个f是使用迭代来求差商的，但是出现了问题。我根据它的提示创建了一个全零数组用于存储运算得到的差商，在某种程度上解决了这个问题。

在解决第3题时，我特意编写了一个算差商的程序和一个4次牛顿插值多项式代入数据画图的程序。差商的程序是修改第2题的牛顿插值程序得到的，这在一定程度上说明，一个程序的功能是可以分开的同时也可以写在一起的。但在写4次多项式代入画图的程序时，并没有参考的我，只能回看书本关于4次牛顿插值的知识，我得到了这个牛顿插值多项式的公式，并发现它的关键就是每一项的系数，而那些系数就是算得的差商，所以，很快，我就写出了4次多项式代入画图的程序。很开心的是，算得的多项式拟合得很好。

标签：yi,xi,end,插值法,多项式,牛顿,插值,Matlab

来源： https://www.cnblogs.com/jianle23/p/12817734.html