本文主要是介绍详细推导BEC和BSC的信道容量,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
介绍
一. 熵的计算公式
二. 互信息
三. 计算BSC的信道容量
四. BEC信道与高斯信道容量
五. 信道传输速率与信道容量
小结
介绍
binary symmetric channel,简称BSC,中文翻译为二进制对称信道。
binary erasure channel,简称BEC,中文翻译为二进制擦除信道。
因为信道传输会出现差错,这是两种最简单的有差错的信道建模方法。
一. 熵的计算公式
香农熵的计算公式如下:
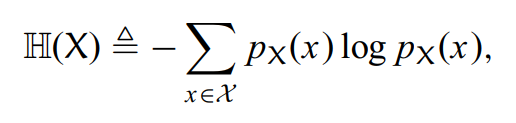
理解:概率乘以概率的对数值,再相加,最后求相反数。
联合熵的计算公式如下:

理解:联合概率乘以联合概率的对数值,再相加,最后求相反数。
条件熵与联合熵之间的关系:
条件熵可以理解为,当已知Y时,X还剩下多少的不确定性。总的不确定性为H(XY),已知Y,所以Y的不确定性H(Y)需要被减掉。
二. 互信息
信息论安全中互信息的计算公式如下:

互信息为熵减去条件熵。
三. 计算BSC的信道容量
假定BSC的转换概率为P,那么可以将输入和输出写成如下表:
| 0 | 1 | |
| 0 | 1-p | p |
| 1 | p | 1-p |
假定输入为均匀且随机的,也就是取0的概率为1/2,取1的概率也为1/2,根据我们的经验此分布有1比特的熵,来利用香农熵公式简单验证一下:

根据BES信道的特征,如果输入是均匀分布,那么输出也是均匀且随机的分布,也就可得:
H(X)=H(Y)=1
X与Y的联合分布为:
| (0,0) | 1/2(1-p) |
| (0,1) | 1/2p |
| (1,0) | 1/2p |
| (1,1) | 1/2(1-p) |
那么可计算联合分布的熵:
带入可得:
其中代表二进制熵。
接着可计算条件熵H(X|Y):
信道容量定义为输入X与输出Y的互信息:
C=I(X;Y)
由此可计算BSC信道容量为:
四. BEC信道与高斯信道容量
假定信道的输入为X,信道的输出为Y,当输入的概率分布Px在不断变化时,则会出现互信息的改变。信道编码定理告诉我们信道容量(channel capacity)等于输入与输出之间最大的互信息。
以上我们证明了BSC的信道容量为:
运用同样的方法可证明,BEC的信道容量为:
其中为擦除概率。
当然在实际网络安全应用中加性高斯白噪声信道(additive white Gaussian noise channel),简称为高斯信道,更为常见。此模型考虑了热噪声和干扰的影响,利用i代表时间,该模型可以表示为:
Yi=Xi+Ni
其中Xi代表输入信号,Ni代表独立随机的高斯变量噪声,分布满足:
实际上如果不外加限制,高斯信道的信道容量可以达到无穷大,所以在实际应用中,通常需要假设平均功率满足如下限制:

利用P代表功率限制,代表噪声方差,那么高斯信道容量可计算为:
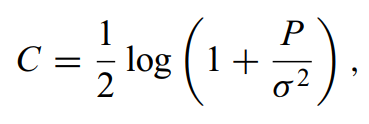
理解:
高斯信道容量的推导有两个关键点:一个是输入需要满足功率限制,第二个是信道是连续的分布。
其实可以借助弱典型集理论和弱渐近等分性(AEP),也可以推导,此处略。
五. 信道传输速率与信道容量
利用R代表信道的可达速率,再引入一个很小的正数
通常都研究渐进性,所以序列长度n足够长,码字则可以总结为:
传输速率与消息熵需要满足:

译码错误率需要足够小,所以可得:
![]()
根据Fano不等式,也就是在已知Y时要求对M的不确定熵趋近于0,所以可得:

接着我们对传输速率进行放缩运算:

最后的不等式来源于马尔科夫链:
![]()
由此可得数据处理的不等式结论,从M-X,其互信息肯定在增加
接着进行放缩:
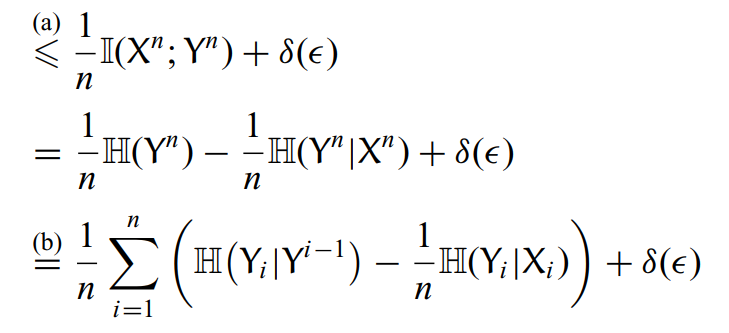
最后的不等式根据信道的离散无记忆特性,分成n次求和
更进一步放缩可得:

最后一个不等式来源于条件概率不会增加熵结论,因为以上的可以随意小,所以可得:
![]()
由此说明了信道传输速率与信道容量之间的关系。
小结
通信的本质是传递消息:

输入序列、信道和输出序列都可以看成随机的。从接收者的角度,总希望能正确的解码结果,也就是误差概率尽可能的小。讨论最简单也是最理想情况就是:一个输出只对应一个输入。
从提高信息传输效率的角度出发,总是希望减少冗余度,也就是压缩,用尽可能少的信道传输符号来传递信源消息,这就是信源编码的作用。
从提高信息抗干扰能力,增强通信可靠性的角度出发,总是希望增加或保留剩余度,这是信道编码要达到的目的,一般是采用冗余编码法,赋予码字自身一定的纠错和检错能力。
提高抗干扰能力往往是以降低信息传输效率为代价的,而为了提高传输效率又往往削弱了其抗干扰能力。这样,设计者在取舍之间就要作均衡考虑。这也是在网络安全领域,安全性与效率性之间的平衡。
信道编码定理的一个简单总结:只要码率小于信道容量,信息就可以通过该信道可靠的传输。此处的可靠代表译码误码率可以接近0
考虑现实的无线通信环境,信道编码定理使用的新思想包括:
- 允许任意小的非0误差概率存在,考虑渐进性;
- 连续使用信道许多次,以保证可以使用大数定理 ,其实也可以看成渐进性;
- 在随机选择的码簿上计算平均误差概率,这样可以使概率对称,而且可以用来证明至少存在一个好的编码。平均性告诉我们有些高,有些低,那么必然存在一个满足的编码方案。
这篇关于详细推导BEC和BSC的信道容量的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






