第一章-Mathematical Models in Mechanics（按照Edexcel课本顺序讲解,没有编辑完）

本文主要是介绍第一章-Mathematical Models in Mechanics（按照Edexcel课本顺序讲解,没有编辑完），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Learning Objective
●理解数学模型如何应用到力学中
●理解假设 （Assumptions）如何在力学模型中利用
●知道7个标准单位以及在derived quantities中的使用。（下面前三个在M1必须掌握）

physical quantity	symbol
meter	m
kilogram	kg
second	s
ampere	A
mole	mol
candela	cd

是米(m),千克(kg),秒(s),安培(A),开尔文(K),摩尔(mol),坎德拉(cd)。

Prior Knowledge Check（预备知识）
1.$5x^2-21x+4=0$
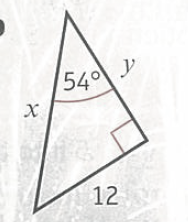
2.

3.30km/h to cm/s
4.0.003806

Example1
The motion of a basketball as it leaves a player’s hand and passes through the net can be modelled using the equation $h=2+1.1x-0.1x^2$, where $h$ m is the height of the basketball above the groupd and $x$ m is the horizontal distance travelled. "

a Find the height of the basketball:

i whenitis released ii at a horizontal distance of 0.5 m.
b Use the model to predict the height of the basketball when it is at a horizontal distance of 15 m

from the player.
c Comment on the validity of this prediction.

Solution
a首先绘制这个图

import numpy as np  
import matplotlib.pyplot as plt  # 定义x的范围  
x = np.linspace(0, 15, 400)  # 定义h函数  
h = 2 + 1.1*x - 0.1*x**2  # 绘制h函数  
plt.figure(figsize=(8,6))  
plt.plot(x, h, label='h(x)')  
plt.title('h(x) = 2 + 1.1x - 0.1x^2')  
plt.xlabel('x')  
plt.ylabel('h(x)')  
plt.grid(True)  
plt.legend()  
plt.show()

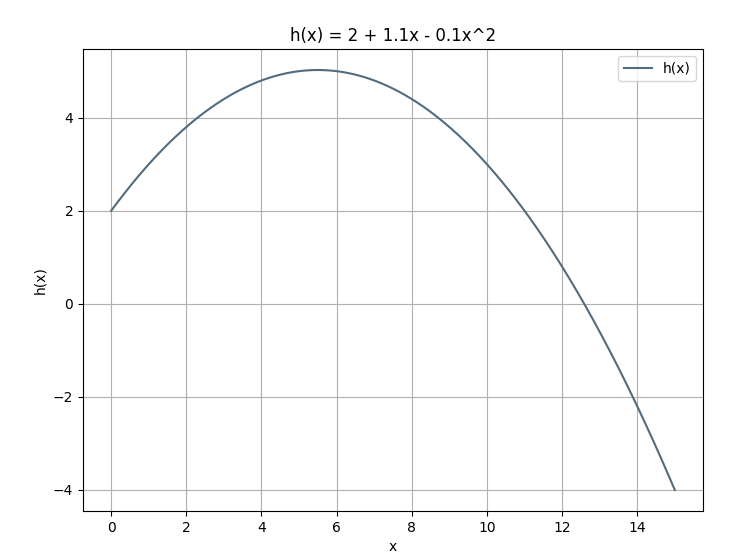
根据图可以知道在y轴上的y=2的地方是篮球起抛点（考试时不要写中文，下同，注意这个只是讲义！）

$\begin{array}{llc}\text{a}& \text{i}& x=0;h=2+0-0\\ & & \text{Height}=2m\end{array}$

ii问的是在水平距离x=0.5的位置，球的高度是多少
$\begin{array}{rl}\text{ii}& x=0.5;h=2+1.1\times 0.5-0.1\times (0.5{)}^2\\ \text{Height}& =2.525m\end{array}$

b Use the model to predict the height of the basketball when it is at a horizontal distance of 15 m from the player.
根据上面画的图可知，球都到地底下了了，所以模型不适用。
b $\begin{array}{l}x=15;h=2+1.1\times 15-0.1\times (15{)}^2\\ \text{Height}=-4m\end{array}$

$\text{c Comment on the validity of this prediction.}$
c Height cannot be negative so the model is not valid when x=15m

这篇关于第一章-Mathematical Models in Mechanics（按照Edexcel课本顺序讲解,没有编辑完）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---