2023.11.22ALP

本文主要是介绍2023.11.22ALP，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

这种压缩方式，就是一位记录小数点后的有效数字位数，一位记录所有的数据

然后复原就是

但会存在误差，因为最后解压缩的时候用到了乘法，但是10不是二进制能精确表示的，所以乘以10就会产生误差 

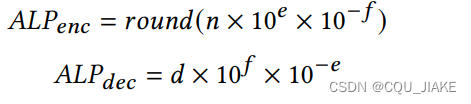
e是什么？ 

IEEE 754

舍入误差和精度损失

1. 舍入误差（Rounding Error）：由于计算机中使用有限的比特数来表示浮点数，而实数是无限精度的，因此在将实数近似表示为浮点数时，会引入舍入误差。舍入误差是由四舍五入或截断操作引起的，这意味着浮点数的实际值与所表示的近似值之间存在差异。

   例如，将0.1这个十进制数转换为二进制浮点数时，由于二进制无法精确表示0.1，会引入舍入误差。在浮点数运算中，舍入误差可能会累积并导致计算结果与预期结果有微小的差异。

2. 精度损失（Precision Loss）：当使用有限精度浮点数表示实数时，会丢失一部分精度。这是因为浮点数的尾数位数是有限的，对于超出尾数位数的小数部分或非常大的数值部分，会进行舍入或截断操作，导致精度损失。

   例如，如果使用单精度浮点数表示非常大或非常小的数值，可能会丢失小数部分的精度或整数部分的精度。这种精度损失可能会导致计算结果的准确性下降。

8.0605的舍入误差

假设我们将8.0605近似表示为单精度浮点数（32位），根据IEEE 754标准，单精度浮点数的尾数位数为23位。

首先，将8.0605转换为二进制表示形式。对于整数部分，它是8的二进制表示形式，即1000。对于小数部分，我们将使用乘2取整法将其转换为二进制。

小数部分的转换过程如下：
0.0605 * 2 = 0.121 (整数部分为0)
0.121 * 2 = 0.242 (整数部分为0)
0.242 * 2 = 0.484 (整数部分为0)
0.484 * 2 = 0.968 (整数部分为0)
0.968 * 2 = 1.936 (整数部分为1)
0.936 * 2 = 1.872 (整数部分为1)
0.872 * 2 = 1.744 (整数部分为1)
0.744 * 2 = 1.488 (整数部分为1)
0.488 * 2 = 0.976 (整数部分为0)
0.976 * 2 = 1.952 (整数部分为1)
0.952 * 2 = 1.904 (整数部分为1)
0.904 * 2 = 1.808 (整数部分为1)

将整数部分的二进制和小数部分的二进制连接起来，得到8.0605的近似单精度浮点数表示为：
1000.00011110001010110111011

由于单精度浮点数只有23位的尾数位数，我们需要将其进行舍入或截断操作以适应这个限制。根据舍入规则，如果尾数位数的下一位大于等于0.5，则进位；否则，舍去。

根据上述表示，第24位是1，大于0.5，因此进行进位操作。所以最终的近似单精度浮点数为：
1000.00011110001010110111100

现在，我们将这个近似单精度浮点数转换回十进制形式，得到近似值为8.060500144958496。

最后，计算舍入误差：
舍入误差 = 实际值 - 近似值
舍入误差 = 8.0605 - 8.060500144958496
舍入误差 ≈ -0.000000144958496

因此，将8.0605近似表示为单精度浮点数时的舍入误差约为-0.000000144958496。

用一个整数d和一个指数e,Penc和Pdec的成功事例取决于两个因素，一个是e的真实精度，一个是n的可见精度。高位数的e可以对所有值有效

高指数位如14，，16，对所有的值都可以到达99的精度。不同的值需要不同的指数位来进行存储，确定这个指数位就是PDE要做的。

但是高指数位使ENC的程序很大

存储64位整数加一位指数比存储64位精度的小数更费空间

ALP存三个参数，一个是指数，一个是因数，一个是位宽

如果数据是重复的，就可以用字典的方式进行编码，用FFOR的方式编码字典；或者使用RLE，然后分别编码运行长度与运行值

如果数据是有序的，可以使用差值编码，而不是FFOR与字典或者RLE

最好的编码方式是使例外的大小总和最小

SIMD

SIMD（Single Instruction, Multiple Data）是一种计算机指令集架构，它允许单条指令同时对多个数据元素执行相同的操作。SIMD的设计目标是提高并行计算的效率，特别适用于处理大规模数据集和执行相似操作的任务。

SIMD指令集架构将多个数据元素打包成矢量（向量），并使用单个指令来操作整个矢量。这种并行操作方式可以在单个时钟周期内同时处理多个数据元素，从而加快计算速度。常见的SIMD指令集架构包括MMX（多媒体扩展）、SSE（Streaming SIMD Extensions）、AVX（Advanced Vector Extensions）等。

SIMD广泛应用于图像处理、数字信号处理、科学计算、多媒体处理等领域，其中需要对大量数据进行相同或相似的操作。它可以加速向量运算、矩阵乘法、图像滤波、音频处理等任务，提高计算效率和性能。

以图像处理为例，SIMD指令集可以同时对像素矢量进行操作，加速图像的处理和转换。例如，可以使用SIMD指令一次性对多个像素进行亮度调整、颜色转换或滤波操作，从而加快图像处理的速度。

需要注意的是，为了充分发挥SIMD指令的优势，程序和算法需要进行适当的优化和向量化。这意味着代码需要被设计为能够利用SIMD指令并行处理数据，以获得最佳的性能提升。

总结来说，SIMD是一种计算机指令集架构，通过在单条指令中同时处理多个数据元素，提供了并行计算的能力。它广泛应用于需要对大规模数据集进行相同或相似操作的任务，加速计算速度和提高性能。

这篇关于2023.11.22ALP的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---