【hiho一下 第四十二周】骨牌覆盖问题·二

本文主要是介绍【hiho一下 第四十二周】骨牌覆盖问题·二，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

原题地址：http://hihocoder.com/contest/hiho42/problem/1
2xN的骨牌问题：http://blog.csdn.net/smile_watermelon/article/details/45151175

题目描述

上一周我们研究了2xN的骨牌问题，这一周我们不妨加大一下难度，研究一下3xN的骨牌问题？
所以我们的题目是：对于3xN的棋盘，使用1x2的骨牌去覆盖一共有多少种不同的覆盖方法呢？
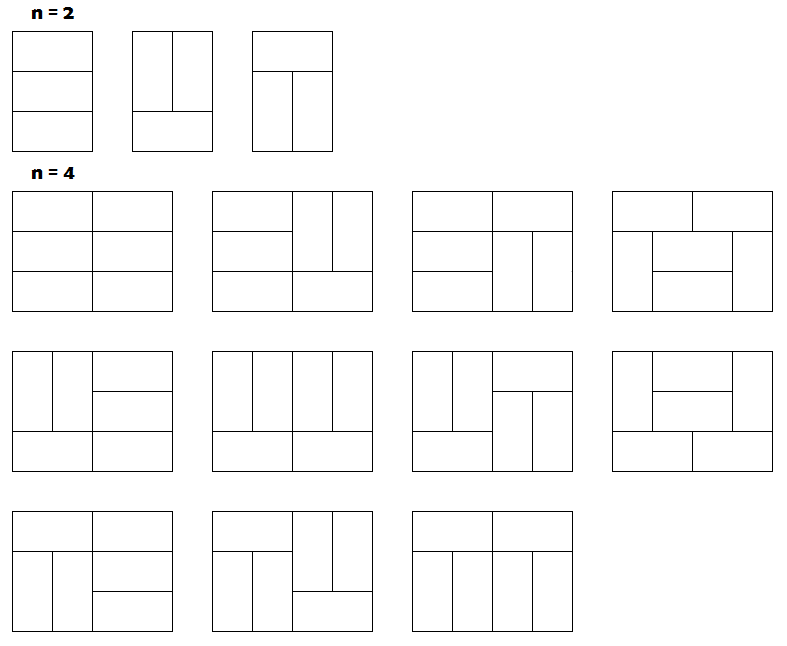
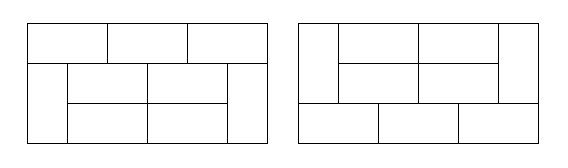
首先我们可以肯定，奇数长度一定是没有办法覆盖的；对于偶数长度，比如2，4，我们有下面几种覆盖方式：【注】原题中此处图片有错误，下图是更正后的图片

输入

第1行：1个整数N。表示棋盘长度。1≤N≤100,000,000

输出

第1行：1个整数，表示覆盖方案数 MOD 12357

样例输入

62247088

样例输出

4037

---

解题思路

原题中有一个解题提示，我看了以后觉得太乱了，非常不好懂，下面是我整理的我的思路。

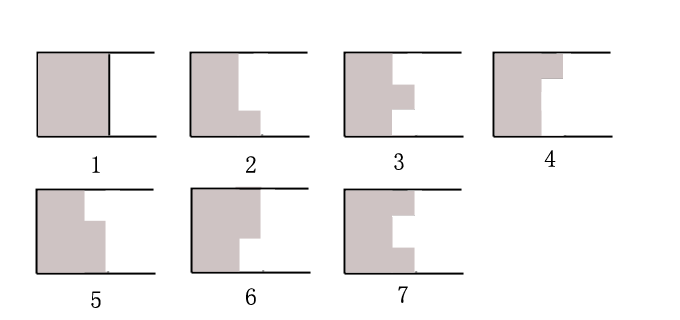
看到这个题，我还是尝试按照动态规划的思想去找一个规律，将问题划归为其子问题，不难发现，如果要将问题划归为子问题的话，需要使得骨牌排列的整齐，如下图1的形式，而不是其他几种形式（灰色部分表示已经摆好骨牌了）：

即，当我们已经把骨牌整齐的排练好某x长度后，剩余的n-x长度即是一个子问题。接下来，我们看有哪些摆放形式可以构成图1中的形式。

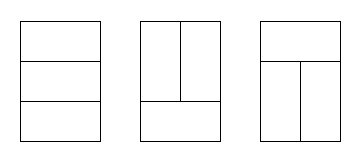
1. 首先，我们当n=2时，我们可以很轻松的找出所有可能的构造形式，如下：
   

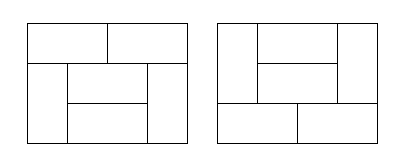
2. 然后我们考虑，是否还有其他形式呢？我们发现当n=4时，有如下两种未出现过的构造形式：
   

3. 接下来还有吗？还有，n=6时，有如下两种未出现过的结构：
   

4. 同理，n=8,10,12,14…时都会新添两种类似步骤2和步骤3中的新的排列方式。

我们需要注意的是，在n增大的同时，除了新增的排列方式之外，原先的排列方式也是存在的。

那么如何推导递归式呢？

我们每次只考虑当前步骤的摆法，然后减去当前步骤占用的空间，然后划归为其子问题。

对于n，我们假设解决方案数目为f(n)。考虑如下：

• 当n为奇数时，不论如何摆放都不可能整齐得把所有位置都摆好，此时f(n)=0
• 当n为正偶数时，如果n>=2，先考虑将其最前面的2个空间摆好，按照上文中的分析有3种摆法，然后问题可归为子问题，即有3*f(n-2)种摆法
• 如果n>=4，再考虑将其前面的4个空间摆好（并且只按上文分析中n=4时新加的两种方式摆放骨牌），按照上文的分析有2中摆法，然后问题可归为子问题，即又有2*f(n-4)种摆法
• 继续判断n>=6，如果成立，则考虑将其前面的6个空间摆好（并且只按上文分析中n=6时新加的两种方式摆放骨牌），按照上文的分析有2中摆法，然后问题可归为子问题，即又有2*f(n-6)种摆法
• 以此类推，直到所有的n长度都按最特殊的摆法摆放，可以有f(n) = 3 * f(n-2) + 2 * f(n-4) + 2 * f(n-6) + … 2 * f(0)
• 特殊的，我们有f(0)=1，即没有空间可摆放骨牌时，其整齐的解决摆放方案有1种（就是什么都不放）

至此，我们有以下递归式：

f(n) =

$$\begin{cases} 1, & \text{if $n$ = 0} \\[2ex] 0, & \text{if $n$ < 0 or n is odd} \\[2ex] 3*f(n-2) + 2*f(n-4) + 2*f(n-6) +... +2*f(0), & \text{otherwise} \end{cases}$$

有了公式之后，我们就可以编程实现了。编程实现上，看起来问题不大，然而，如果我们使用常规递归方式实现的话，问题很大。例如，题目中给出的测试数据是62247088，如果我们使用递归方法来实现代码的话，其调用过程大概如下，f(62247088)先调用f(62247086)，f(62247086)中又调用f(62247084)，f(62247084)中又调用f(62247082)……，这个过程中程序要不停的压栈，实在是难以想象。事实上，我一开始代码就是这么写的，程序跑了一会儿之后，我的小破本儿竟然直接黑屏重启了 : (

该如何优化代码呢？

传统的递归过程是f(n)调用f(n-1)，f(n-2)…，我们何不尝试反过来求解呢？先求f(2)，然后是f(4)，然后是f(6)，直到求出f(n)为止。

另外，我们还可以发现如下规律：

• f(n) = 3 * f(n-2) + 2 * f(n-4) + … + 2 * f(0)
• f(n+2) = 3 * f(n) + 2 * f(n-2) + 2 * f(n-4) + … + 2 * f(0)
• f(n+4) = 3 * f(n+2) + 2 * f(n) + 2 * f(n-2) + 2 * f(n-4) + … + 2 * f(0)

因此我们可以利用在计算f(n)时的数据来计算f(n+2)，f(n+4)…这样我们优雅的解决了两个问题：第一，不用递归调用函数来求解子问题；第二，不用开辟一个O(n)的空间来存储子问题的值。

最后，不要忘记对结果取模（MOD 12357）

代码

#include <stdio.h>int main() {int n;scanf("%d", &n);        // 输入数据if (n & 1 || n < 0) {   // 如果是奇数或者负数，输出0printf("0\n");} else if (n == 0) {      // 如果是0，输出1printf("1\n");} else {// sum存储f(i)，last存储f(i-2)，lastSum存储2*(f(i-4)+f(i-6)+...+f(0))// 初始化值i=2，last=f(i-2)=f(0)=1,lastSum=0int i = 2, sum, last = 1, lastSum = 0;// 循环计算f(i)，直到f(n)for (; i <= n; i += 2) {// 计算f(i)，f(i)=3*f(i-2)+2*(f(i-4)+f(i-6)+...+f(0))sum = 3 * last + lastSum;   sum %= 12357;       // 取模// 更新lastSum，即2*f(i-2)+2*(f(i-4)+f(i-6)+...+f(0))lastSum += 2 * last;    lastSum %= 12357;   // 取模// 更新last，即last=f(i)，以备计算f(i+2)时使用last = sum;}printf("%d\n", sum);    // 输出}return 0;
}

hihocoder平台代码提交 ACCEPT
时间：1520ms
内存：0MB

---

个人学习记录，如有错误请指正
// sfg1991@163.com
// 2015-04-20

这篇关于【hiho一下 第四十二周】骨牌覆盖问题·二的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---