Leetcode 887题：鸡蛋掉落问题

这道题难度为hard，问题求解相对复杂，但也是面试高频题，因此有必要总结一下。

1.题目描述

给你 k 枚相同的鸡蛋，并可以使用一栋从第 1 层到第 n 层共有 n 层楼的建筑。

已知存在楼层 f ，满足 0 <= f <= n ，任何从 高于 f 的楼层落下的鸡蛋都会碎，从 f 楼层或比它低的楼层落下的鸡蛋都不会破。

每次操作，你可以取一枚没有碎的鸡蛋并把它从任一楼层 x 扔下（满足 1 <= x <= n）。如果鸡蛋碎了，你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎，则可以在之后的操作中 重复使用 这枚鸡蛋。

请你计算并返回要确定 f 确切的值 的 最小操作次数 是多少？

示例 1：

输入：k = 1, n = 2
输出：2
解释：鸡蛋从 1 楼掉落。如果它碎了，肯定能得出 f = 0 。 否则，鸡蛋从 2 楼掉落。如果它碎了，肯定能得出 f = 1 。 如果它没碎，那么肯定能得出 f = 2 。 因此，在最坏的情况下我们需要移动 2 次以确定 f 是多少。  

示例 2： 

输入：k = 2, n = 6
输出：3

示例 3：

输入：k = 3, n = 14
输出：4

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/super-egg-drop

2.思路分析 

状态：很明显，就是当前拥有的鸡蛋数 K 和需要测试的楼层数 N。随着测试的进行，鸡蛋个数可能减少，楼层的搜索范围会减小，这就是状态的变化。

选择：其实就是去选择哪层楼扔鸡蛋。回顾刚才的线性扫描和二分思路，二分查找每次选择到楼层区间的中间去扔鸡蛋，而线性扫描选择一层层向上测试。不同的选择会造成状态的转移。

现在明确了「状态」和「选择」，动态规划的基本思路就形成了：肯定是个二维的 dp 数组或者带有两个状态参数的 dp 函数来表示状态转移；外加一个 for 循环来遍历所有选择，择最优的选择更新状态。

定义dp函数：dp(k, n)表示当有k个鸡蛋面对n层楼时，至少需要dp(k, n)次操作才能得到答案 

状态转移： 

• 如果鸡蛋碎了，那么鸡蛋的个数 K 应该减一，搜索的楼层区间应该从 [1..N] 变为 [1..i-1] 共 i-1 层楼；
• 如果鸡蛋没碎，那么鸡蛋的个数 K 不变，搜索的楼层区间应该从 [1..N] 变为 [i+1..N] 共 N-i 层楼。

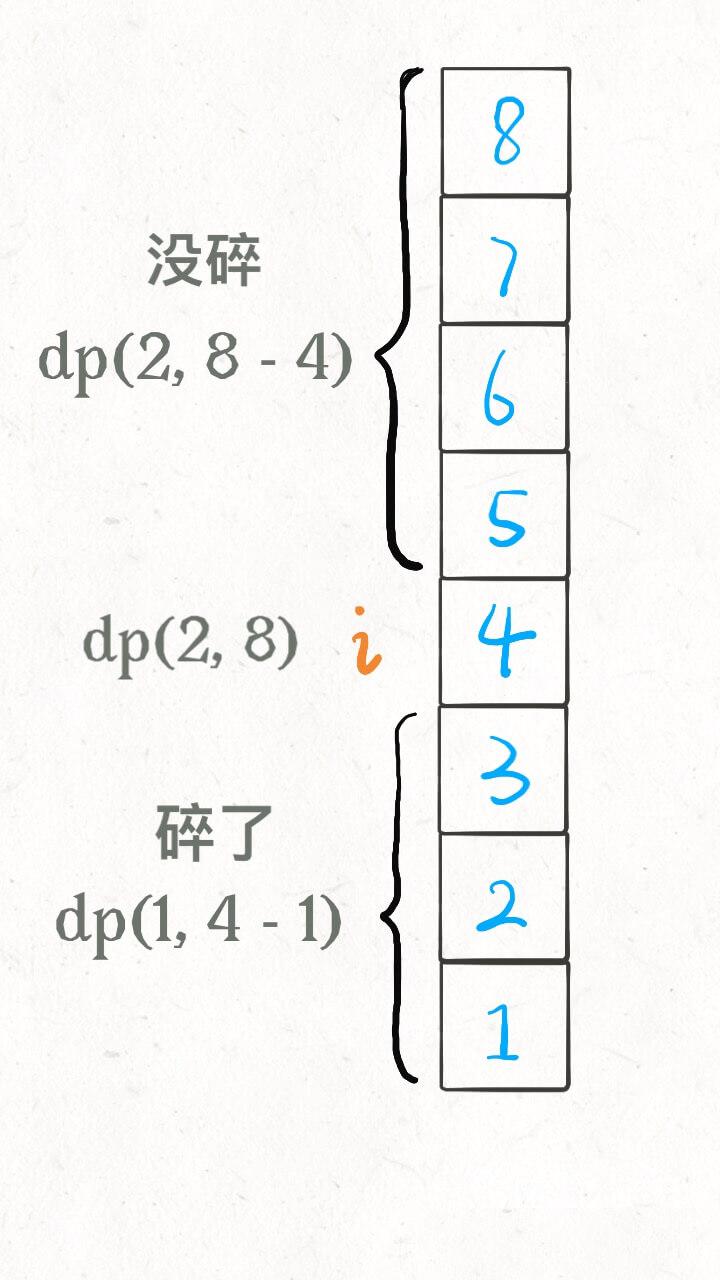
base case：当楼层数 N 等于 0 时，显然不需要扔鸡蛋；当鸡蛋数 K 为 1 时，显然只能线性扫描所有楼层： 

if(k == 1) return 0;

if(n == 0) return 0;

优化：添加备忘录，消除重叠子问题

3.解答 

 完整代码（java）：

class Solution {//动态规划 + 备忘录//定义备忘录，消除重叠子问题HashMap<String, Integer> memo = new HashMap<>();public int superEggDrop(int k, int n) {return dp(k, n);}//辅助方法：dp()表示当有k个鸡蛋面对n层楼时，至少需要dp(k, n)次操作才能得到答案public int dp(int k, int n){//base caseif(k == 1){//剩一个鸡蛋时只能线性搜索return n;}if(n == 0){//没鸡蛋时无法操作return 0;}String key = k + "," + n;//如果备忘录有搜索记录，直接返回if(memo.containsKey(key)){return memo.get(key);}//状态转移int res = Integer.MAX_VALUE;for(int i = 1; i <= n; i++){//在第i层扔鸡蛋//如果碎了，鸡蛋数减一，搜索楼层范围缩小至i-1//如果没碎，鸡蛋数不变，搜索楼层范围变为n-ires = Math.min(res, 1 + Math.max(dp(k - 1, i - 1), dp(k, n - i)));}//将结果添加到备忘录memo.put(key, res);return res;}
}

动态规划算法的时间复杂度就是子问题个数 × 函数本身的复杂度。

这里 dp 函数中有一个 for 循环，所以函数本身的复杂度是 O(N)。

子问题个数也就是不同状态组合的总数，显然是两个状态的乘积，也就是 O(KN)。

所以算法的总时间复杂度是 O(K*N^2), 空间复杂度 O(KN)。（这个时间复杂度大概率是要超时了）

4.二分搜索优化 

首先简述一下原始动态规划的思路：

1、暴力穷举尝试在所有楼层 1 <= i <= N 扔鸡蛋，每次选择尝试次数最少的那一层；

2、每次扔鸡蛋有两种可能，要么碎，要么没碎；

3、如果鸡蛋碎了，F 应该在第 i 层下面，否则，F 应该在第 i 层上面；

4、鸡蛋是碎了还是没碎，取决于哪种情况下尝试次数更多，因为我们想求的是最坏情况下的结果。

核心的状态转移方程：

如果能够理解这个状态转移方程，那么就很容易理解二分查找的优化思路。

首先我们根据 dp(K, N) 数组的定义（有 K 个鸡蛋面对 N 层楼，最少需要扔几次），很容易知道 K 固定时，这个函数随着 N 的增加一定是单调递增的，无论你策略多聪明，楼层增加测试次数一定要增加。

那么注意 dp(K - 1, i - 1) 和 dp(K, N - i) 这两个函数，其中 i 是从 1 到 N 单增的，如果我们固定 K 和 N，把这两个函数看做关于 i 的函数，前者随着 i 的增加应该也是单调递增的，而后者随着 i 的增加应该是单调递减的：

 这时候求二者的较大值，再求这些最大值之中的最小值，其实就是求这两条直线交点，也就是红色折线的最低点嘛。

熟悉二分搜索的同学肯定敏感地想到了，这不就是相当于求 Valley（山谷）值嘛，可以用二分查找来快速寻找这个点的，直接看代码吧，整体的思路还是一样，只是加快了搜索速度：

class Solution {//动态规划 + 二分搜索 + 备忘录//二分搜索原理//dp(k - 1, i - 1)函数是单调递增的//dp(k, n - i)函数是单调递减的//则max(dp(k - 1, i - 1), dp(k, n - i))是一条V形线//则min(max + 1)是V形线的最低点//定义备忘录，消除重叠子问题HashMap<String, Integer> memo = new HashMap<>();public int superEggDrop(int k, int n) {return dp(k, n);}//辅助方法：dp()表示当有k个鸡蛋面对n层楼时，至少需要dp(k, n)次操作才能得到答案public int dp(int k, int n){//base caseif(k == 1){//剩一个鸡蛋时只能线性搜索return n;}if(n == 0){//没鸡蛋时无法操作return 0;}String key = k + "," + n;//如果备忘录有搜索记录，直接返回if(memo.containsKey(key)){return memo.get(key);}//状态转移int res = Integer.MAX_VALUE;//二分搜索int low = 1, hight = n;while(low <= hight){int mid = low + (hight - low) / 2;int broken = dp(k - 1, mid - 1); //鸡蛋碎了int not_broken = dp(k, n - mid); //鸡蛋没碎if(broken > not_broken){hight = mid - 1;res = Math.min(res, broken + 1);}else{low = mid + 1;res = Math.min(res, not_broken + 1);}}//将结果添加到备忘录memo.put(key, res);return res;}
}

同理，算法的总时间复杂度是 O(K*N*logN), 空间复杂度 O(KN)。效率上比之前的算法 O(KN^2) 要高效一些。 

5.进一步优化（换种思路定义状态转移方式） 

上文定义的dp数组可表示为：

p[k][n] = m

# 当前状态为 k 个鸡蛋，面对 n 层楼

# 这个状态下最少的扔鸡蛋次数为 m 

按照这个定义，就是确定当前的鸡蛋个数和面对的楼层数，就知道最小扔鸡蛋次数。最终我们想要的答案就是 dp(K, N) 的结果。

这种思路下，肯定要穷举所有可能的扔法的，用二分搜索优化也只是做了「剪枝」，减小了搜索空间，但本质思路没有变，还是穷举。

现在，我们稍微修改 dp 数组的定义，确定当前的鸡蛋个数和最多允许的扔鸡蛋次数，就知道能够确定 F 的最高楼层数。具体来说是这个意思：

dp[k][m] = n
# 当前有 k 个鸡蛋，可以尝试扔 m 次鸡蛋
# 这个状态下，最坏情况下最多能确切测试一栋 n 层的楼

# 比如说 dp[1][7] = 7 表示：
# 现在有 1 个鸡蛋，允许你扔 7 次;
# 这个状态下最多给你 7 层楼，
# 使得你可以确定楼层 F 使得鸡蛋恰好摔不碎
# （一层一层线性探查嘛）

这其实就是我们原始思路的一个「反向」版本，我们先不管这种思路的状态转移怎么写，先来思考一下这种定义之下，最终想求的答案是什么？

我们最终要求的其实是扔鸡蛋次数 m，但是这时候 m 在状态之中而不是 dp 数组的结果，可以这样处理：

int superEggDrop(int K, int N) {

    int m = 0;
    while (dp[K][m] < N) {
        m++;
        // 状态转移...
    }
    return m;
}

题目不是给你 K 鸡蛋，N 层楼，让你求最坏情况下最少的测试次数 m 吗？while 循环结束的条件是 dp[K][m] == N，也就是给你 K 个鸡蛋，测试 m 次，最坏情况下最多能测试 N 层楼。

注意看这两段描述，是完全一样的！所以说这样组织代码是正确的，关键就是状态转移方程怎么找呢？还得从我们原始的思路开始讲。之前的解法配了这样图帮助大家理解状态转移思路：

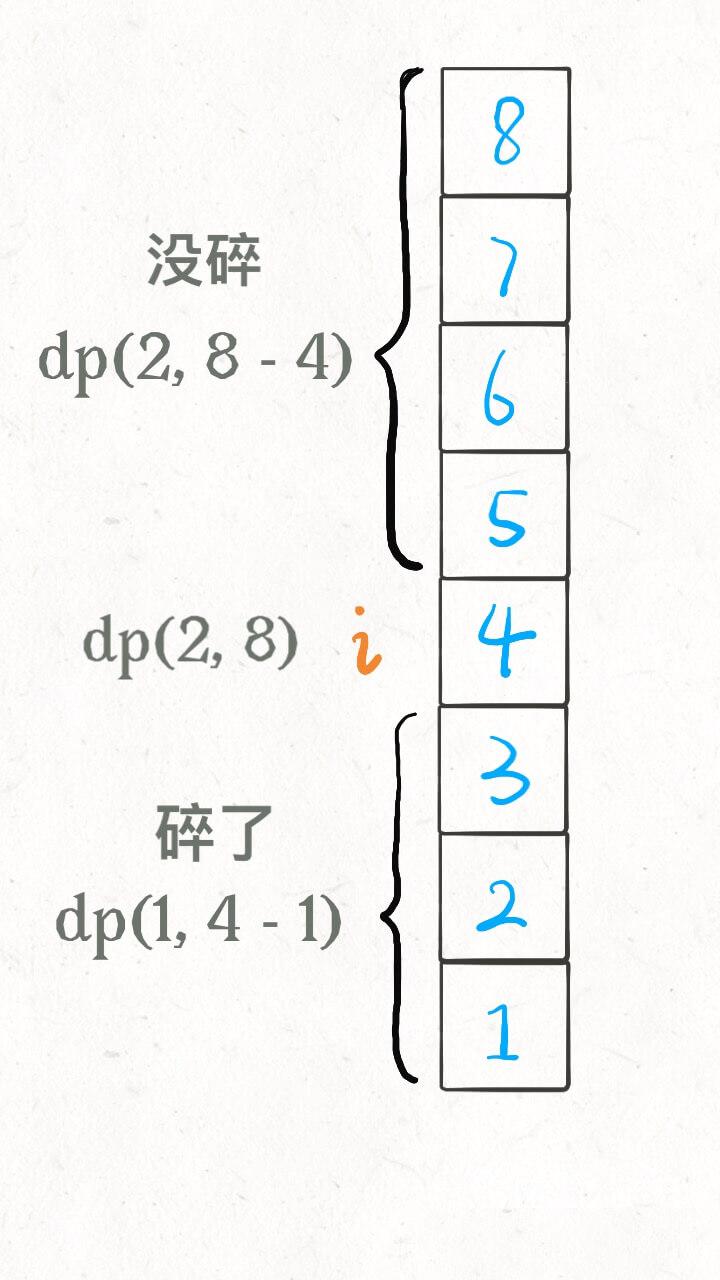
这个图描述的仅仅是某一个楼层 i，原始解法还得线性或者二分扫描所有楼层，要求最大值、最小值。但是现在这种 dp 定义根本不需要这些了，基于下面两个事实：

1、无论你在哪层楼扔鸡蛋，鸡蛋只可能摔碎或者没摔碎，碎了的话就测楼下，没碎的话就测楼上。

2、无论你上楼还是下楼，总的楼层数 = 楼上的楼层数 + 楼下的楼层数 + 1（当前这层楼）。

根据这个特点，可以写出下面的状态转移方程：

dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1

dp[k][m - 1] 就是楼上的楼层数，因为鸡蛋个数 k 不变，也就是鸡蛋没碎，扔鸡蛋次数 m 减一；

dp[k - 1][m - 1] 就是楼下的楼层数，因为鸡蛋个数 k 减一，也就是鸡蛋碎了，同时扔鸡蛋次数 m 减一。

 PS：这个 m 为什么要减一而不是加一？之前定义得很清楚，这个 m 是一个允许的次数上界，而不是扔了几次。

 至此，整个思路就完成了，只要把状态转移方程填进框架即可：

class Solution {//重新定义状态转移方程//如果鸡蛋没碎，测楼上，dp[k_num][m - 1]是楼上的楼层数//如果鸡蛋碎了，测楼下，dp[k_num - 1][m - 1]是楼下的楼层数//总楼层数dp[k_num][m] = dp[k_num][m - 1] + dp[k_num - 1][m - 1] + 1;public int superEggDrop(int k, int n) {//定义dp数组：dp[k][m] = n表示有k个鸡蛋，最多允许测试m次，可以找出楼层高为n的楼栋中的答案int[][] dp = new int[k + 1][n + 1];//base case//dp[0][...]和dp[...][0]在定义dp时已全部初始化为0了//状态转移int m = 0;while(dp[k][m] < n){m++;for(int k_num = 1; k_num <= k; k_num++){dp[k_num][m] = dp[k_num][m - 1] + dp[k_num - 1][m - 1] + 1;}}return m;}
}

算法的时间复杂度很明显就是两个嵌套循环的复杂度 O(KN)。