本文主要是介绍【概率论基础】标本空间与事件 | Sample Space and Event,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

前言:
个人学习笔记,由于是国外教材,所以翻译的数学名词可能与国内教材上的有些许出入。
目录
前言:
0x00 定义
0x01 复原提取和非复原提取
0x02 和事件和交事件
0x03 余事件和差事件
0x04 互斥事件和两两互斥事件
0x05 划分(partition)
0x00 定义
概率(probability)
事件在一定条件下发生的可能性程度以数值表现形式,称为概率。
统计(statistics)
从社会现象到自然现象的各种数据,按照一定的系统,以数值的形态进行分析和表达。
概率现象(random phenomenon)
在社会现象和自然现象中,结果不是预先确定的现象,即结构受到某种不确定性影响的现象,称为概率现象。
概率实验(random experiment)
结果表现为概率现象的实验、观察或调查,称为概率实验。(比如:掷硬币、掷色子、抽牌)
标本空间(sample space)
从概率实验中可以获得的所有可能结果的集合,称为概率是实验的标本空间,用符号 或
表示。
标本点(sample point)
標本空間的每个元素称为一个样本点,用 等表示。
事件(event)
标本空间的部分集合(子集),满足一定条件的特定样本点的集合称为事件,用大写字母 等表示。
全事件(total event)
标本空间 为全事件。
空事件(empty event)
记为 。
根源事件(elementary event)
由一个样本点组成的事件称作根源事件。
参考:
① 抛硬币概率实验中的样本空间为:
(硬币正面记为H,反面即为T)
② 单次掷骰子的样本空间为:

例题:
① 求出硬币反复抛3次的概率实验中的标本空间 .

② 请求出至少出现一次正面(H) 的事件 A.
![]()
③ 请求出背面(T) 比正面(H) 出现的次数多的事件 B.
![]()
0x01 复原提取和非复原提取
再概率实验中多次重复同一实验时:
复原提取(replacement)
将提取的内容返回并提取下一个的方式,我们称之为 复原提取。(replacement)
(放回抽样)
非复原提取(without replacement)
提取下一个而不返回提取的方式称为非复原提取。
(不放回抽样)
0x02 和事件和交事件
对于标本空间 的部分集合的两个事件 A 和 B:
和事件(union of event)
A和B的合事件:发生事件A或事件B的事件
![]()
交事件(intersection of events)
A和B的交事件:事件A和事件B同时发生的事件称为交事件
![]()
参考:
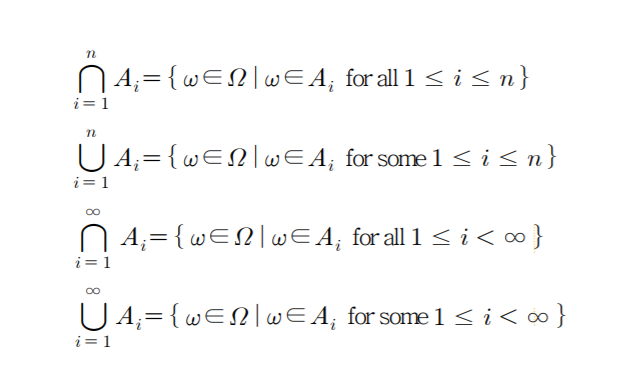
0x03 余事件和差事件
对于标本空间 的部分集合的两个事件 A 和 B:
余事件(complementary event)
事件A没有发生的事件:
![]()
差事件(difference of event)
发生事件A但是没有发生事件B的事件:
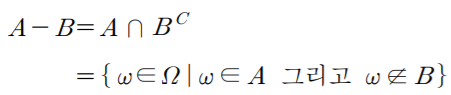
0x04 互斥事件和两两互斥事件
互斥事件(mutually exclusive events)
标本空间 的部分集合中的两个事件 A 和 B 同时没有发生时,则
![]() 时,A B 两事件被称为 互斥事件。
时,A B 两事件被称为 互斥事件。
两两互斥事件(pairwisely mutually exclusive events)
对于标本空间 的部分集合(子集)的
个事件的
,
![]() 时,
时, 被称为成对互斥事件。
(任意两个都互斥)
0x05 划分(partition)
对于标本空间 的部分集合(子集)的
个事件的
的以下两个条件:
① 是两两互斥事件。则
![]()
② 若满足 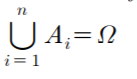 ,我们称
,我们称![]() 是标本空间
是标本空间 的划分(完备事件群)。
即试验中的若干个事件,它们互斥且至少有一事件发生。
例题:投币三次,如果定义正面出现的次数 的事件为
,请证明该事件是标本空间
的划分。
为两两互斥事件,且
是
的划分。
参考资料:
Heels L Z W H. Probability and statistics[M]. 4. .
百度百科[EB/OL]. []. https://baike.baidu.com/.
本篇完。
这篇关于【概率论基础】标本空间与事件 | Sample Space and Event的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





