力扣LCR 166. 珠宝的最高价值（java 动态规划）

本文主要是介绍力扣LCR 166. 珠宝的最高价值（java 动态规划），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

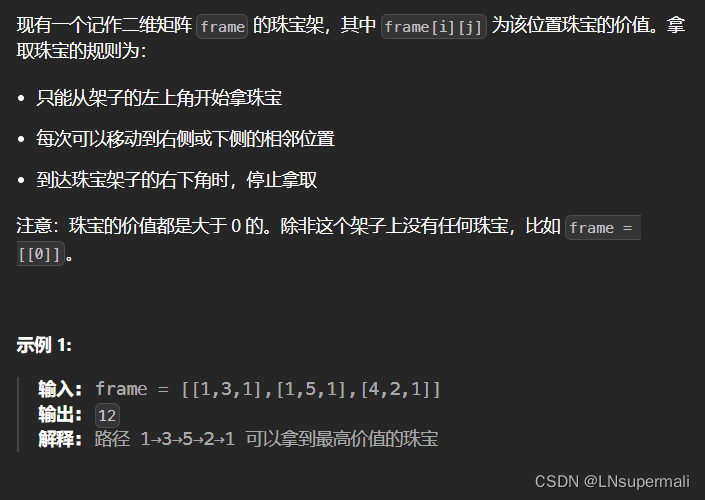
Problem: LCR 166. 珠宝的最高价值

文章目录

解题思路
思路
解题方法
复杂度
Code

解题思路

思路

改题目与本站64题实质上是一样的，该题目在64题的基础上将求取最小路径和改成了求取最大路径和。具体实现思路如下：

1.定义一个int类型的二维数组dp大小为给定矩阵frame的行数与列数。该数组用于记录每个当前阶段的最大路径和（也是本题目的最大价值）
2.动态转移方程为**dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + frame[i][j];**即当前位置（也可以记作阶段）最大值每次取出其上方，和左侧的较大值的一个与当前frame位置值作和；
3.由于dp数组中第一行与第一列无法直接执行动态转移方程，要对其初始化：第一行每个位置值为依次向右累加；第一列每个位置值为依次向下累加
3.最后返回dp数组中的最后一个值即可。

解题方法

1.定义数组frame的行数rows与列数columns；并定义一个int变量temp用于记录累加和
2.定义并初始化int类型数组dp初始化为new int[rows][colunms]
3.初始化dp的第一行与第一列，在for循环中使temp依次累加当前第一行（列）位置的值，并赋值给当前dp数组位置；
4.从dp数组的第二行（索引为1）开始执行动态转移方程dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + frame[i][j];，最后返回dp[rows - 1][columns - 1];

复杂度

时间复杂度:

$O (MN)$ ,其中 $M$ 为数组frame的行数, $N$ 为其列数

空间复杂度:

$O (MN)$

Code

class Solution {/*** The maximum path sum is obtained using dynamic programming** @param frame Given matrix* @return int*/public int jewelleryValue(int[][] frame) {int rows = frame.length;int columns = frame[0].length;int temp = 0;//Records the current maximum path sumint[][] dp = new int[rows][columns];//Handle the first row and columnfor (int i = 0; i < columns; ++i) {temp += frame[0][i];dp[0][i] = temp;}temp = 0;for (int j = 0; j < rows; ++j) {temp += frame[j][0];dp[j][0] = temp;}//Dynamic transfer equationfor (int i = 1; i < rows; ++i) {for (int j = 1; j < columns; ++j) {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + frame[i][j];}}return dp[rows - 1][columns - 1];}
}