本文主要是介绍无失真编码之霍夫曼编码的python实现——数字图像处理,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
原理
无失真编码是一种数据压缩技术,其中原始数据在压缩后可以完全无损地恢复。霍夫曼编码是一种广泛使用的无失真编码方法。它基于字符出现的频率构建一个最优的前缀编码树,其中没有任何编码是另一个编码的前缀。这样,即使在压缩后,原始数据也可以完全无误地被解码和恢复。霍夫曼编码的原理可以分为以下几个步骤:
1. 统计字符频率
首先,统计待编码数据中每个字符的出现频率。这个频率信息是构建霍夫曼树的基础。
2. 构建霍夫曼树
霍夫曼树的构建过程如下:
为数据中的每个不同字符创建一个叶子节点,并将其频率作为节点的权重。
将所有节点按照频率(权重)排序,放入一个优先队列(如最小堆)中。
当队列中有多于一个节点时,执行以下操作:
从队列中移除两个频率最低的节点。
创建一个新的内部节点,其频率是这两个节点频率之和。
将这两个节点作为新节点的子节点,一个为左子节点,一个为右子节点。
将新节点重新加入队列。
这个过程重复进行,直至队列中只剩下一个节点,这个节点成为霍夫曼树的根节点。
3. 生成霍夫曼编码
对霍夫曼树进行遍历(例如深度优先遍历),为每个叶子节点分配一个二进制编码。从根到叶子的每条路径定义了相应字符的编码。一般约定,向左的路径代表’0’,向右的路径代表’1’。
4. 编码数据
根据霍夫曼树得到的编码,替换原始数据中的每个字符,完成数据的编码过程。
解码数据
由于霍夫曼编码是前缀编码,任何编码都不是另一个编码的前缀,因此可以无误地从编码数据中恢复原始数据。
优点
霍夫曼编码的主要优点在于其根据字符出现的频率生成编码,使得频率高的字符具有较短的编码,频率低的字符具有较长的编码。这种方法通常能生成接近最优的无失真压缩率。
应用
霍夫曼编码在文件压缩(如 ZIP 文件格式)和多媒体数据压缩(如 JPEG 和 MP3)中得到了广泛应用。由于其无失真的特性,它在需要完整恢复原始数据的场景中非常有用。
代码要求实现下图
提示
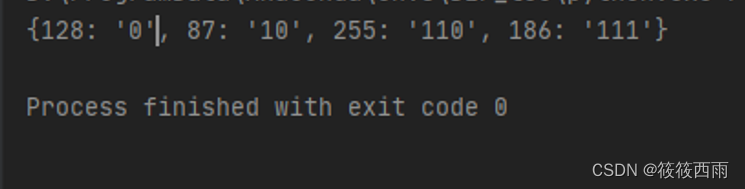
结果显示了图像中灰度值经过霍夫曼编码后的码表,如灰度值128被编码为长度为1的码字“0”,灰度值87被编码为长度为2的码字“10”等。注意:霍夫曼编码所构造的码表不是唯一的,你的实验结果可能和上图所示不同。
第一步,读入图像并计算其直方图,统计其各灰度值出现的概率(次数)。注意,统计直方图所用函数为hist = cv2.calcHist([img], [0], None, [256], [0, 256])。
第二步,针对各灰度值出现的概率大小进行排序、合并(信源化简),此过程构造出一颗霍夫曼树,可以使用python中queue模块中的PriorityQueue数据结构编写代码。
第三步,根据上一步得到的霍夫曼树进行逆向编码,得到每一个灰度值对应的码字。这一步可以从根节点出发,通过不断给其子节点添加1比特码字的嵌套迭代过程实现。
python代码
import cv2
import numpy as np
from queue import PriorityQueuedef huffman_tree_to_table(root, prefix, table):if type(root[1]) != tuple:table[root[1]] = prefixelse:huffman_tree_to_table(root[1][0], prefix+'0', table)huffman_tree_to_table(root[1][1], prefix+'1', table)return tableimg = cv2.imread('Fig0801.tif', 0)
hist = cv2.calcHist([img], [0], None, [256], [0, 256])
gray_value = np.flatnonzero(hist)queue_ = PriorityQueue()
for value in gray_value:queue_.put((hist[value], value))while queue_.qsize() > 1:node1 = queue_.get()node2 = queue_.get()new_count = node1[0] + node2[0]queue_.put((new_count, (node1, node2)))root = queue_.get()
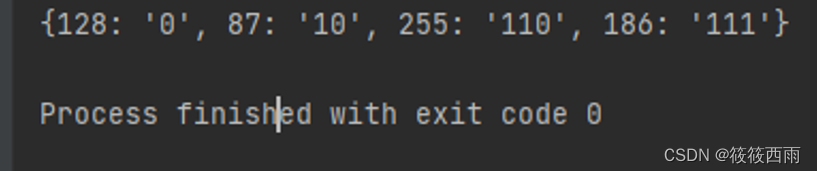
table = huffman_tree_to_table(root, '', {})print(table)结果展示
这篇关于无失真编码之霍夫曼编码的python实现——数字图像处理的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






