本文主要是介绍POJ1141,brackets sequence,括号比配的问题,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
POJ1141,brackets sequence,括号比配的问题。这题与上面两题有点像,有了上面两题的基础,分析此题也不难。好了,还是看题吧。
求:为了使原来的括号序列匹配,需求加入了最少括号数,而且要知道具体怎么加括号。
因为这题需要打印最终的匹配结果,所以在用DP的时候要多记录一些信息,以方便打印。
设原括号序列为S1 S2 … Sn。
如果S1和 Sn匹配,则相当于求S2 … Sn-1的括号匹配情况。这时最终的匹配结果是:先打印S1,再打印S2 … Sn-1的括号匹配结果,最后打印Sn。
如果S1和 Sn不匹配,怎么办呢?如果把S1 S2 … Sn从中间某个位置(比如Sk)分成两截,问题就变成S1 … Sk和Sk+1 … Sn的情况了。也就是说,把原问题划分成了两个结构相同的子问题。那么,具体从哪划分呢?好像没有什么信息可用,那就从1…n对k进行枚举。因为最终要打印结果,所以还要记录k的值。这时最终的结果是:先打印S1 … Sk的匹配情况,再打印Sk+1 … Sn的匹配情况。
设dp( i, j )表示Si … Sj匹配时,所要加入的最少括号数。
状态转换方程:
dp( i, j ) = dp( i+1, j-1 ) ifS1和 Sn匹配
dp( i, j ) = Min( dp( i, k ) + dp( k+1, j ) ), 其中 i <= k < j ifS1和 Sn不匹配
下图是字符串( [ ( ]的计算过程。
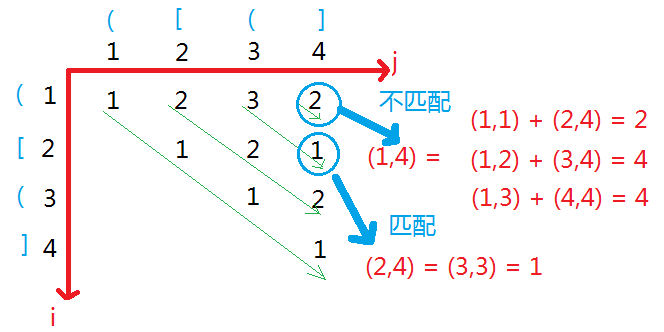
编程实现:算法是有了,不过具体的编程实现还是有点小技巧。嘿嘿,当前主要是针对初学者来说,大牛可完全无视之。
初始条件。当i==j时,dp( i, j ) = ?想想实际情况,只剩下一个括号时,不管它是什么当然不匹配啦。所以必须找到它的另一半才行,故dp( i, i ) = 1
计算顺序。应该沿Z型计算,即i、j之间相差1,i、j之间相差2,…
打印结果。使用递归打印。
package com.sjyttkl.algorithm.dp;/*** POJ1141,brackets sequence,括号比配的问题。这题与上面两题有点像,有了上面两题的基础,分析此题也不难。好了,还是看题吧。* * 求:为了使原来的括号序列匹配,需求加入了最少括号数,而且要知道具体怎么加括号。* * 因为这题需要打印最终的匹配结果,所以在用DP的时候要多记录一些信息,以方便打印。* * 设原括号序列为S1 S2 … Sn。* * 如果S1和 Sn匹配,则相当于求S2 … Sn-1的括号匹配情况。这时最终的匹配结果是:先打印S1,再打印S2 … Sn-1的括号匹配结果,最后打印Sn。* * 如果S1和 Sn不匹配,怎么办呢?如果把S1 S2 … Sn从中间某个位置(比如Sk)分成两截,问题就变成S1 … Sk和Sk+1 …* Sn的情况了。也就是说* ,把原问题划分成了两个结构相同的子问题。那么,具体从哪划分呢?好像没有什么信息可用,那就从1…n对k进行枚举。因为最终要打印结果,所以还要记录k的值* 。这时最终的结果是:先打印S1 … Sk的匹配情况,再打印Sk+1 … Sn的匹配情况。* * 设dp( i, j )表示Si … Sj匹配时,所要加入的最少括号数。* * 状态转换方程:* * dp( i, j ) = dp( i+1, j-1 ) ifS1和 Sn匹配* * dp( i, j ) = Min( dp( i, k ) + dp( k+1, j ) ), 其中 i <= k < j ifS1和 Sn不匹配* * 下图是字符串( [ ( ]的计算过程。* * * * 编程实现:算法是有了,不过具体的编程实现还是有点小技巧。嘿嘿,当前主要是针对初学者来说,大牛可完全无视之。* * 初始条件。当i==j时,dp( i, j ) = ?想想实际情况,只剩下一个括号时,不管它是什么当然不匹配啦。所以必须找到它的另一半才行,故dp( i,* i ) = 1* * 计算顺序。应该沿Z型计算,即i、j之间相差1,i、j之间相差2,…* * 打印结果。使用递归打印。 pos* */
public class POJ1141
{// (](]]]][]public static String str = "(](]";static char[] chars = str.toCharArray();static int len = str.length();// 设str = S0 S1 S2 ... Sn;// 则dp[i][j]表示Si...Sj要构成最短正则括号序列所要增加的括号数目static int[][] dp = new int[len][len];// pos[i][j]表示划分str成为两部分的最佳位置static int[][] pos = new int[len][len];public static void main(String[] args){System.out.println(str);DPSolve(len);System.out.println("--------------------------------");for (int i = 0; i < len; i++){for (int j = 0; j < len; j++){System.out.print(dp[i][j] + " ");}System.out.println();}System.out.println("--------------------------------");for (int i = 0; i < len; i++){for (int j = 0; j < len; j++){System.out.print(pos[i][j] + " ");}System.out.println();}Print(0, len - 1);}private static void DPSolve(int len){// 只要一个括号时,必不匹配,要匹配需要另外一个括号for (int i = 0; i < len; i++){dp[i][i] = 1;}// 沿之字形填写dp[][]for (int k = 1; k < len; k++){for (int i = 0, j = i + k; i < len && j < len; i++, j++){// 这里 的j 是为了设置只计算上三角的内容// 因为要求最小,现将dp[i][j]设置为最大dp[i][j] = Integer.MAX_VALUE;if ((chars[i] == '(' && chars[j] == ')') || (chars[i] == '[' && chars[j] == ']')){dp[i][j] = dp[i + 1][j - 1];pos[i][j] = -1;}// 注意:这里不要用else// 因为要求最小,所以即使比配也要进行下面的处理:例如[][]// 枚举tmp,求划分str的最佳位置for (int temp = i; temp < j; temp++){if (dp[i][j] > dp[i][temp] + dp[temp + 1][j]){//System.out.println(dp[i][temp] + " -------- " + dp[temp + 1][j]);dp[i][j] = dp[i][temp] + dp[temp + 1][j];//System.out.println(dp[i][j]);pos[i][j] = temp;}}}}}// 根据dp[][],打印结果private static void Print(int left, int right){if (left <= right){// 当只有一个括号时,直接打印if (left == right){if (chars[left] == '(' || chars[left] == ')'){System.out.print("()");}if (chars[left] == '[' || chars[left] == ']'){System.out.print("[]");}} else{// 如果首尾括号匹配if (pos[left][right] == -1){System.out.print(chars[left]);Print(left + 1, right - 1);System.out.println(chars[right]);} else{Print(left, pos[left][right]);//看上面的,是以right村进去的,tempPrint(pos[left][right]+1, right);}}}}}
这篇关于POJ1141,brackets sequence,括号比配的问题的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






