李超树模板 / p4097

前言

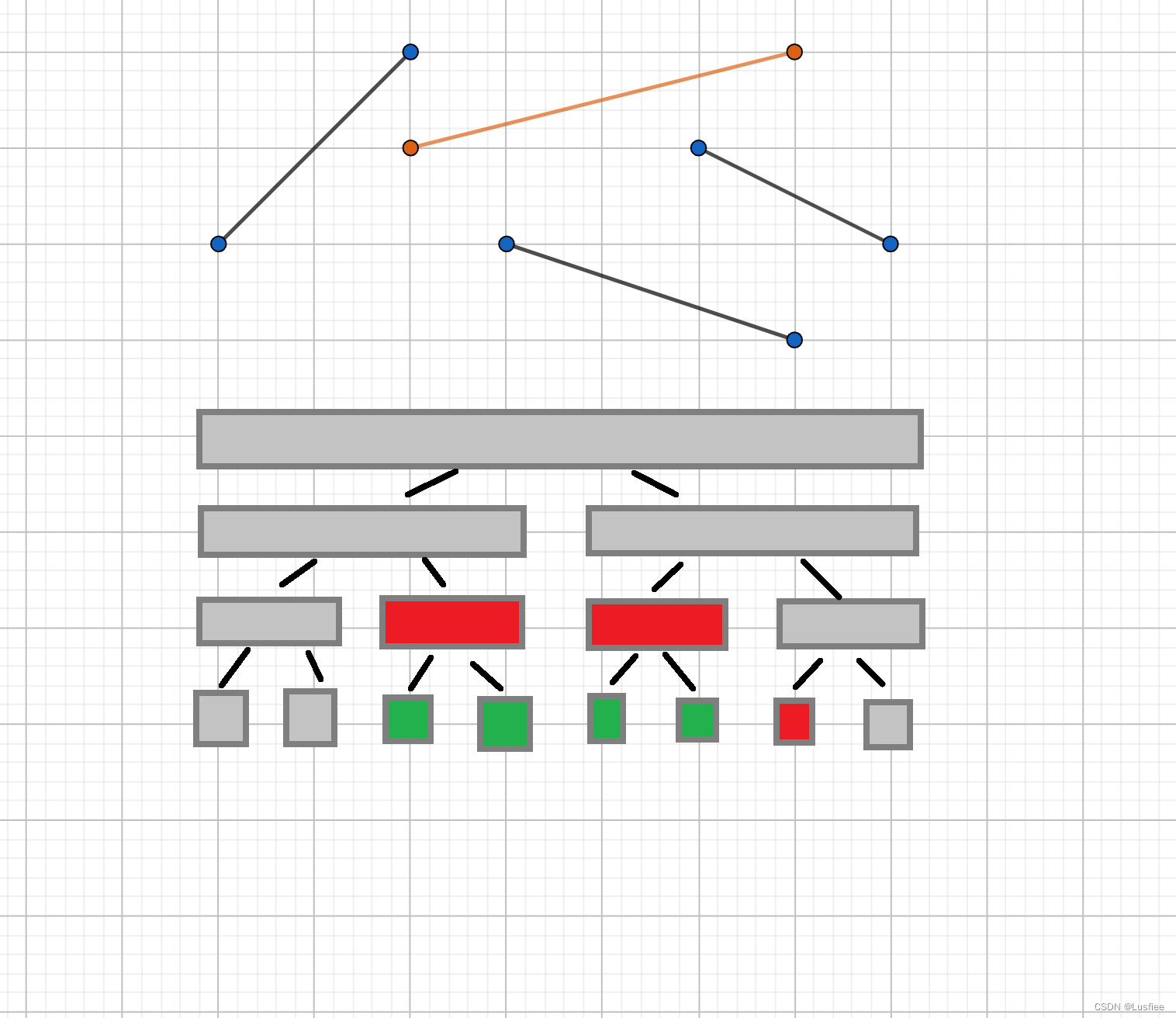
李超树是一种维护平面线段的数据结构

可以将一次函数存储至线段树中

其可以实现如下功能：

1. 在平面上增加一条线段（$O({\log }^{2}n)$）
2. 查询与 $x=k$ 相交的线段中纵坐标最大（小）的一条 （$O(\log n)$）

不过遗憾的是，不支持已增加线段的修改、删除

其具体实现与常规线段树比较类似

通过建树获得区间的树形结构

而增添一条线段则意味着对线段的定义域进行区间修改

修改时分为 4 种情形，依次讨论即可修改成功

查询时支持单点查询，对覆盖此节点的树进行查询即可

一、题目

模板题：洛谷-p4097

二、思路及代码

1.思路

很模板的一道题，不过要注意其要求强制在线

2.代码

代码如下：

#include <bits/stdc++.h>
#define int long long
#define pdd pair<double, double>
using namespace std;const double eps = 1e-8;
const int mod1 = 39989;
const int mod2 = 1e9;
const int maxn = 1e5 + 5;
int n, lastans, cnt;pdd l[maxn];
double cal(int id, int x) { return l[id].first * x + l[id].second; }
bool judge(int id1, int id2, int x) {double f1 = cal(id1, x), f2 = cal(id2, x);return fabs(f1 - f2) <= eps ? id1 > id2 : f1 < f2;
}struct node {int val;int l, r;node(int _val = 0, int _l = 0, int _r = 0) : val(_val), l(_l), r(_r) {}
};
struct segtree {node t[maxn << 2];void build(int rt, int l, int r) {t[rt].l = l, t[rt].r = r;if (t[rt].l == t[rt].r) return;int mid = (l + r) >> 1;build(rt << 1, l, mid);build(rt << 1 | 1, mid + 1, r);}void update(int rt, int l, int r, int x) {int mid = (t[rt].l + t[rt].r) >> 1;if (l <= t[rt].l && t[rt].r <= r) {  // 4 种情形, 1 种不存在if (judge(t[rt].val, x, mid)) swap(x, t[rt].val);if (judge(x, t[rt].val, t[rt].l) && judge(x, t[rt].val, t[rt].r)) return;if (judge(t[rt].val, x, t[rt].l)) update(rt << 1, l, r, x);if (judge(t[rt].val, x, t[rt].r)) update(rt << 1 | 1, l, r, x);return;}if (l <= mid) update(rt << 1, l, r, x);if (r > mid) update(rt << 1 | 1, l, r, x);return;}int query(int rt, int pos) {if (t[rt].l == t[rt].r) return t[rt].val;int mid = (t[rt].l + t[rt].r) >> 1;int ret = 0;if (mid >= pos)ret = query(rt << 1, pos);elseret = query(rt << 1 | 1, pos);if (judge(ret, t[rt].val, pos)) ret = t[rt].val;return ret;}
};
signed main() {//   freopen(".in", "r", stdin);//   freopen(".out", "w", stdout);ios::sync_with_stdio(0);cin.tie(0), cout.tie(0);segtree tr;tr.build(1, 1, mod1);lastans = cnt = 0;cin >> n;while (n--) {int op;cin >> op;if (op == 0) {int x;cin >> x;x = (x + lastans - 1 + mod1) % mod1 + 1;lastans = tr.query(1, x);cout << lastans << endl;} else if (op == 1) {int x0, x1, y0, y1;cin >> x0 >> y0 >> x1 >> y1;x0 = (x0 + lastans - 1 + mod1) % mod1 + 1;x1 = (x1 + lastans - 1 + mod1) % mod1 + 1;y0 = (y0 + lastans - 1 + mod2) % mod2 + 1;y1 = (y1 + lastans - 1 + mod2) % mod2 + 1;if (x0 > x1) swap(x0, x1), swap(y0, y1);cnt++;double k, b;if (x0 == x1)k = 0, b = max(y0, y1);else {k = (double)(y1 - y0) / (double)(x1 - x0);b = (double)y1 - (double)x1 * k;}l[cnt] = {k, b};tr.update(1, x0, x1, cnt);}}return 0;
}