【模拟电路】常见电学定律 戴维宁定理、诺顿定理、基尔霍夫定律

本文主要是介绍【模拟电路】常见电学定律 戴维宁定理、诺顿定理、基尔霍夫定律，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、戴维宁定理
二、诺顿定理
三、基尔霍夫定律

一、戴维宁定理

任何复杂电路可以等效为一个电压源和一个电阻器组成

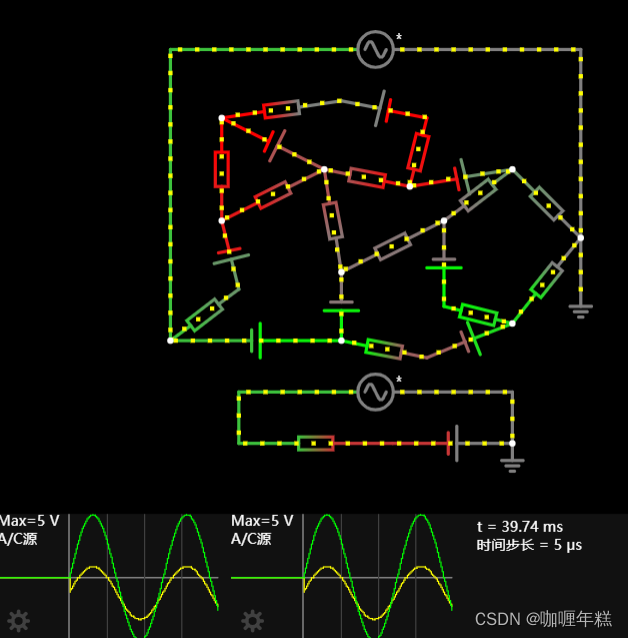
德维宁定理（Thevenin’s Theorem）是电路理论中的一个基本定理，它提供了一种简化复杂线性电路的方法。德维宁定理的主要思想是将线性电路替代为等效的单一电压源和串联电阻，这个等效电路对于外部电路来说与原始电路是等效的。

德维宁定理的表述：

德维宁定理可以表述为以下两个等效性质：

1. 任何线性、双端口电路都可以被一个电压源和串联电阻的等效电路替代。

2. 这个等效电路在两个端口的观察点上对外部电路是透明的。

德维宁定理的数学表达：

对于线性电路，德维宁定理可以用以下等式表示：

$$V_{\text{th}}=V_{\text{oc}}$$

$$R_{\text{th}}=\frac{V_{\text{oc}}}{I_{\text{sc}}}$$

其中：

• ($V_{\text{th}}$) 是电压源的电压，也就是电路的开路电压（Open Circuit Voltage）。
• ($V_{\text{oc}}$) 是电路的开路电压。
• ($R_{\text{th}}$) 是电路的等效电阻，也就是电路在观察端口时看到的电阻。
• ($I_{\text{sc}}$) 是电路的短路电流，也就是在观察端口短路时流过的电流。

应用：

1. 电路简化： 德维宁定理允许将复杂的线性电路简化为一个等效电路，这在分析和设计电路时非常有用。

2. 电路仿真： 在电路仿真中，德维宁定理可以用于替代大规模复杂电路，从而降低仿真的计算复杂度。

3. 电路设计： 在电路设计中，德维宁定理可以帮助工程师更容易地理解电路行为，并在设计过程中进行有效的优化。

总的来说，德维宁定理是电路理论中一个非常有用的工具，它提供了简化复杂电路的方法，使得电路分析和设计变得更加可行。

二、诺顿定理

任何复杂电路可以等效为一个电流源和一个电阻器组成

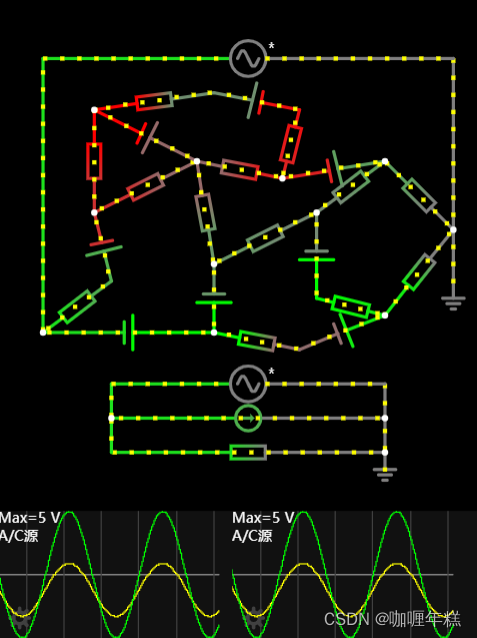
诺顿定理（Norton’s Theorem）是电路理论中的另一个基本定理，与德维宁定理类似，用于简化复杂线性电路。诺顿定理提供了将线性电路替代为等效电流源和并联电阻的方法，这个等效电路对于外部电路来说与原始电路是等效的。

诺顿定理的表述：

诺顿定理可以表述为以下两个等效性质：

1. 任何线性、双端口电路都可以被一个电流源和并联电阻的等效电路替代。

2. 这个等效电路在两个端口的观察点上对外部电路是透明的。

诺顿定理的数学表达：

对于线性电路，诺顿定理可以用以下等式表示：

$$I_{\text{N}}=I_{\text{sc}}$$

$$R_{\text{N}}=\frac{V_{\text{oc}}}{I_{\text{sc}}}$$

其中：

• ($I_{\text{N}}$) 是电流源的电流，也就是电路的短路电流（Short Circuit Current）。
• ($I_{\text{sc}}$) 是电路的短路电流。
• ($R_{\text{N}}$) 是电路的等效电阻，也就是电路在观察端口时看到的电阻。
• ($V_{\text{oc}}$) 是电路的开路电压，也就是电路的开路电压。

应用：

1. 电路简化： 诺顿定理允许将复杂的线性电路简化为一个等效电路，这在分析和设计电路时非常有用。

2. 电路仿真： 在电路仿真中，诺顿定理可以用于替代大规模复杂电路，从而降低仿真的计算复杂度。

3. 电路设计： 在电路设计中，诺顿定理可以帮助工程师更容易地理解电路行为，并在设计过程中进行有效的优化。

与德维宁定理一样，诺顿定理是电路理论中一个非常有用的工具，它提供了简化复杂电路的方法，使得电路分析和设计变得更加可行。

三、基尔霍夫定律

对于电路中任一节点,流入节点的电流之和必等于流出该节点的电流之和

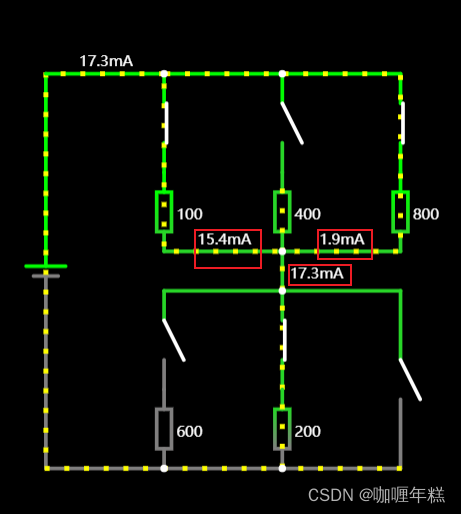
基尔霍夫定律是电路理论中的两个基本定律，分别为基尔霍夫电流定律（Kirchhoff’s Current Law，KCL）和基尔霍夫电压定律（Kirchhoff’s Voltage Law，KVL）。这两个定律由德国物理学家古斯塔夫·基尔霍夫（Gustav Kirchhoff）提出，对于分析复杂电路网络和解决电路问题非常重要。

1. 基尔霍夫电流定律（KCL）：

KCL表述为：在任何电路网络中，进入任意节点的电流的总和等于离开该节点的电流的总和。数学表达式为：

$$\sum _{n=1}^N{I}_n=0$$

其中 ($I_n$) 是进入节点的电流，(N) 是节点上连接的支路的数目。基尔霍夫电流定律反映了电流在节点处的守恒原理。

2. 基尔霍夫电压定律（KVL）：

KVL表述为：在任何闭合电路回路中，沿着电路中的任何闭合路径，通过电路元件的电压之和等于该路径上电压源的总和。数学表达式为：

$$\sum _{m=1}^M{V}_m=\sum _{k=1}^K{E}_k$$

其中 ($V_m$) 是通过电阻、电感或电容等元件的电压，($E_k$) 是路径上的电压源的电压。基尔霍夫电压定律反映了电压在闭合回路中的守恒原理。

应用：

1. 电路分析： 基尔霍夫定律是解析电路的强大工具，可用于分析复杂电路网络中的电流和电压分布。

2. 电路设计： 在设计电路时，基尔霍夫定律可以帮助工程师理解电路中各个元件之间的关系，确保电路的正常工作。

3. 故障排除： 基尔霍夫定律在故障排除过程中也非常有用，可以帮助确定电路中的故障点和电流、电压的分布情况。

基尔霍夫定律是电路理论的基石，为工程师和学生提供了理解和分析电路的重要工具。这些定律对于处理各种电路问题和设计电子系统至关重要。

这篇关于【模拟电路】常见电学定律 戴维宁定理、诺顿定理、基尔霍夫定律的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---