c语言aoe网的关键路径,AOE网求关键路径 c++代码

####题目： 给定10个结点以及结点间的权值，试着求解其任意两点间的关键路径。 ####分析： AOE网原本是存在入点和出点的，这里求“任意节点”，所以会出现不存在的情况。(虽然我觉得这部分不是很必要…)

基本步骤参考了这篇，写得非常好，一个例子远比大段文字描述来得清晰明了。

由于上面那篇文章里的例子是9个点，而题目要求的是10个点，我在v1前面加了一个v0，对结果没有什么影响。

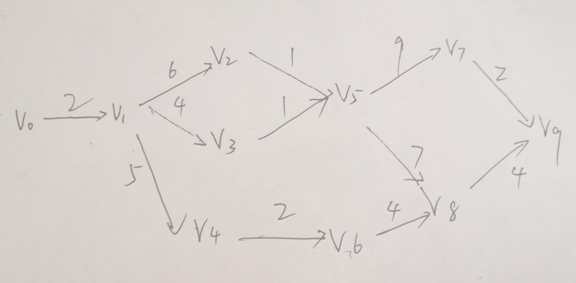
代码如下：

/*算法：

1.输入边数m;

2.初始化权重d[i][j]为max(0<=i

3.输入每条边的起点u终点v及其权重w，设置d[u][v]=w;

4.输入要查询的两点first和last;

5.初始化的earliest[i]=0; latest[i]=max; path[i]=max(0<=i<10);

6.从k=first开始(earliest[first]=0)，递归查找下一个节点i，然后计算各个点最早开始的时间earliest[i]，如果earliest[k]+d[k][i]>earliest[i]则更新earliest[i];如果发现没有任何节点i与k相连，则输出“路径不存在”;

7. 从k=last开始(latest[last]=earliest[last])，递归查找上一个节点i，然后计算各个点最晚开始的时间latest[i]，如果latest[k]-d[i][k]

8. 从k=first开始，循环查找下一个节点i，如果latest[i]-d[k][i]==earliest[k]，则k->i为关键路径，把i加入到path中。

9.打印输出path的内容

*/

#include

using namespace std;

#define max 1000000

int d[10][10];

int earliest[10];

int latest[10];

int path[10];

void findEarliest(int k,int last);

void findLatest(int k,int first);

bool flag=false;//用于判断是否存在关键路径

int main(){

int i,j,k,m,n=10;

int u,v,w;

int first,last,count=0;

int next;

cout<

cin>>m;

for(i=0;i

for(j=0;j

d[i][j]=max;

}

cout<

for(i=0;i

cin>>u>>v>>w;

d[u][v]=w;

}

cout<

cin>>first>>last;

for(i=0;i<10;i++){

earliest[i]=0;

latest[i]=max;

path[i]=max;

}

k=first;path[0]=k;count=1;

findEarliest(k,last);

if(!flag){

cout<

return 0;

}

k=last;latest[k]=earliest[k];

findLatest(k,first);

k=first;

while(k!=last){

for(i=0;i<10;i++){

if(d[k][i]!=max&&(latest[i]-d[k][i]==earliest[k])){

path[count++]=i;

k=i;

break;

}

}

}

cout<

for(i=0;path[i]!=last;i++){

cout<";

}

cout<

}

void findEarliest(int k,int last){

if(k==last)

return;

flag=false;

for(int i=0;i<10;i++){

if(d[k][i]

flag=true;

if((earliest[k]+d[k][i])>earliest[i])

earliest[i]=earliest[k]+d[k][i];

findEarliest(i,last);

}

}

//如果flag没有在循环中被修改为ture，则说明没有节点与k相连(即没有进入if语句内，函数返回不再进行递归)，然后在主函数中判断flag的值来决定是否继续

}

void findLatest(int k,int first){

if(k==first)

return;

for(int i=0;i<10;i++){

if(d[i][k]

if(latest[k]-d[i][k]

latest[i]=latest[k]-d[i][k];

findLatest(i,first);

}

}

}

####结果截图：

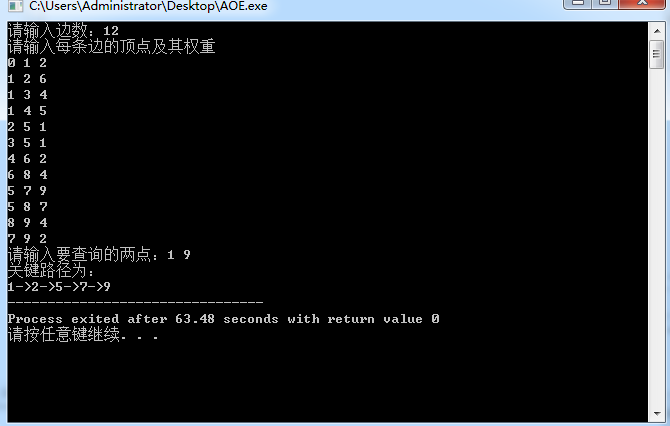
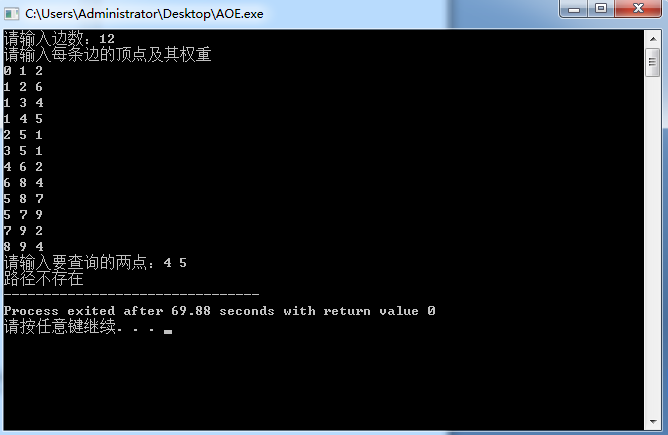
####反思： 采用递归和大量循环遍历在时间上效率很低。本题只有十个点，如果数据规模较大，改成用指针查找或许比较快，但是数据结构的建立就比较麻烦了。 ####本文是个人学习记录，如有错误请指出！