交通 | 顶刊OR论文：轨道交通客流控制新策略解读

论文解读：李净滢，王子旋，李旭强

编者按：

高峰时段客流拥挤一直是大城市轨道交通面临的重要挑战，这不仅会增加人群踩踏事故风险，还导致上下游车站服务水平的巨大差异。为了解决这一问题，近年来轨道交通界对设计科学合理的客流控制策略极为关注。今年，《Operations Research》顶刊上发表的一期专题文章，提出了一类新型客流控制策略，旨在通过针对不同站点制定差异化的乘客上车比例，来提高列车总载客量，并同时将以往文献中被忽视的运载服务公平性问题纳入考虑。这一创新性的研究为轨道交通客流控制领域带来了新的启示，为城市轨道交通系统的改进和优化提供了有力支持。

引言

针对地铁客流需求的随机性和动态性特点，本文考虑列车到达每个站点获知该站的实时客流需求，建立了带服务水平约束的随机动态规划模型，目标是最大化列车总载客量，并满足每个起讫点（origin-destination， OD）乘客的服务水平约束，即保证每个OD乘客的上车比例（填充率）不低于某一固定数值。论文从理论上证明了任意给定服务水平可行的充要条件，并据此设计了基于实时需求信息的的客流控制策略，以实现对高峰时段客流量的精准控制。通过提高列车总载客量，地铁系统可以运输更多乘客，从而减少高峰时段的客流拥挤，提升整体运营效率。与此同时，通过保证每个OD乘客的上车比例，能够使得乘客获得更为公平的公共交通服务，从而提升城市公共交通系统的满意度和便利性。

一、模型介绍

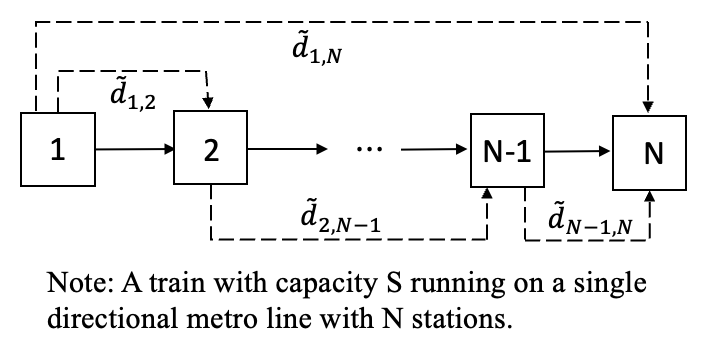
1. 模型假设

• 如上图所示，假设在一条有$N$个车站的单向地铁线路上，一辆容量为$S$的列车依次停靠每个车站从而接收乘客上车，并将其运送到下游终点站；
• 假设从车站 $i$出发到终点站 $j$的客流量 ${\tilde{d}}_{i,j}$为服从均值 ${\bar{d}}_{i,j}$和累积分布函数 $F_{i,j}(\cdot )$的随机数，那么列车在整个运营途中和在第 $i$站的客流需求向量可分别表示为$\tilde{\mathbf{d}}:=\left({\tilde{d}}_{1,2},\dots ,{\tilde{d}}_{N-1,N}\right)$$和$${\tilde{\mathbf{d}}}_{i,\bullet }:=\left({\tilde{d}}_{i,i+1},\dots ,{\tilde{d}}_{i,N}\right)$$
• 假设列车在第 $i$站停靠时，从 $i$站出发的所有乘客的目的地是已知（文章也进一步探讨了乘客目的地未知的情况）。决策者需要为每一个OD对 $(i,j)$确定差异化的客流量接受率 $x_{i,j}(\tilde{\mathbf{d}})$，使得该策略能够最大化总载客数量并满足每个OD的填充率要求。令 $\mathbf{x}$表示为模型的决策变量。

2. 可行解条件

在任意客流需求 $\tilde{\mathbf{d}}$下，车站$i$可以接收的乘客数量不能超过列车的剩余容量，并且该车站出发每个OD的比例也不能超过1.0。对于每一个车站 $i=1,...,N$而言，如果其对应的客流控制决策${\mathbf{x}}_{i,\bullet }$都在如下公式（1）表示的可行域内，则称该策略下的$\mathbf{x}$是一个可行解。

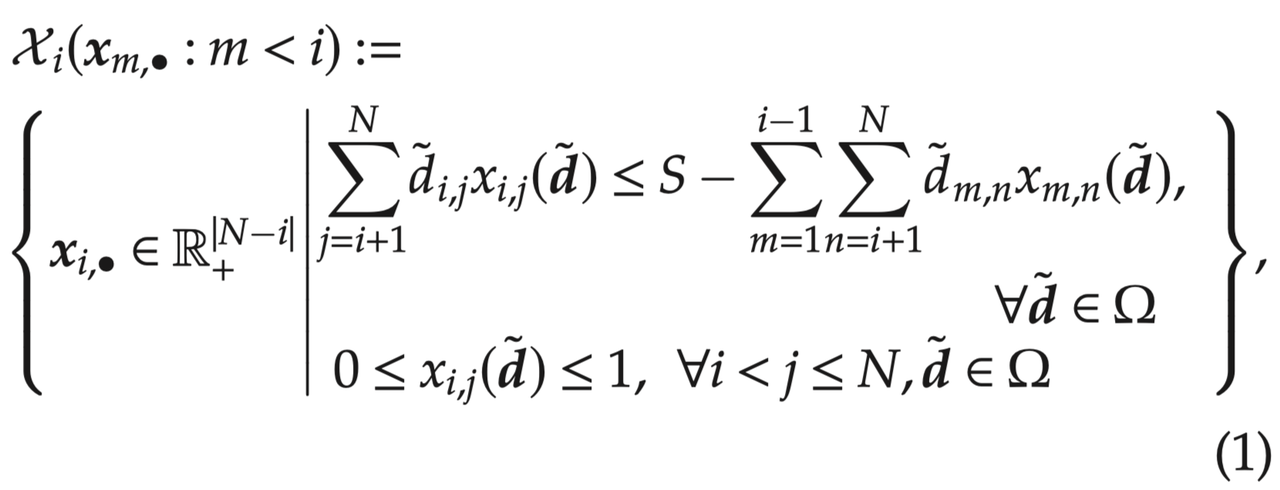
3. 目标函数

决策者旨在设计列车运营途中的客流控制策略，从而实现期望上车人数的最大化。令$r_{i,j}$ 表示将一名乘客从起始站 $i$运送到目的站 $j$所获得的收益，则该问题可以简化为如下的多阶段随机动态规划模型，目标则是找到 $\mathbf{x}$使其最优化。

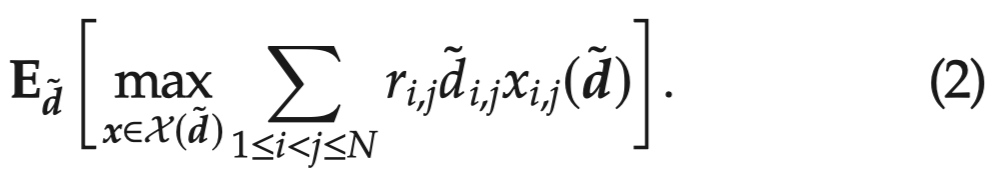
4. 预设填充率要求

论文在模型中添加预设的客流填充率目标约束来保证运载服务公平化。具体而言，令$\mathbf{\beta }=\left({\beta }_{1,2},\dots ,{\beta }_{N-1,N}\right)$表示预设的客流填充率目标，其规定了每个OD对$(i, j) $客流需求被满足的最小比例，如公式（3）所示。

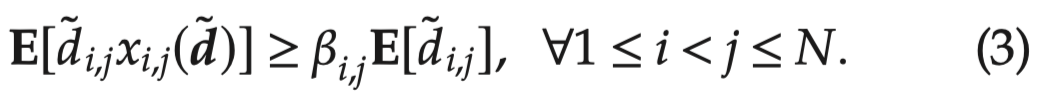
二、求解方法

上述公式$(1),(2),(3)$共同构成了论文要研究的考虑公平性的在线客流控制问题 (OPFCwF)。为求解该问题，论文首先设计了一个随机算法1，来确保任何给定的填充率目标都是可以达到的。支撑这个算法的充分必要条件可以参考原文的定理1以及给出的详细证明，这里简单介绍组成这个算法最重要的一个部分：“债务”自适应策略(DAA)。

“债务”（Debt）在文章里形象地被定义为实际运送的乘客量与填充率所要求运送的乘客量的差值，那么样本$t$阶段下OD对$(i,j)$的“债务”被表示为$R_{i,j}(t):={\tilde{d}}_{i,j}(t)\left[{\beta }_{i,j}^{\prime }-x_{i,j}(t)\right]$。在样本$t+1$阶段开始时，平均“债务”取从样本$1$到$t$所有“债务”的平均值，即${\hat{\alpha }}_{i,j}(t+1):=\frac{1}{t}{\sum }_{s=1}^t{R}_{i,j}(s)$。显而易见的，当${\hat{\alpha }}_{i,j}(t+1)$大于0的时候，此前对于前$t$个时段的客流量控制策略未能达到目标填充率。因此，在第$t+1$个时段，将优先满足具有更大正“债务”的OD对$(i,j)$客流需求，从而最终满足所有OD对的填充率目标。

这里将$f_{a}(\boldsymbol{\alpha}(t+1))
$表示为第$t+1$个样本阶段收益最大化问题的最优值

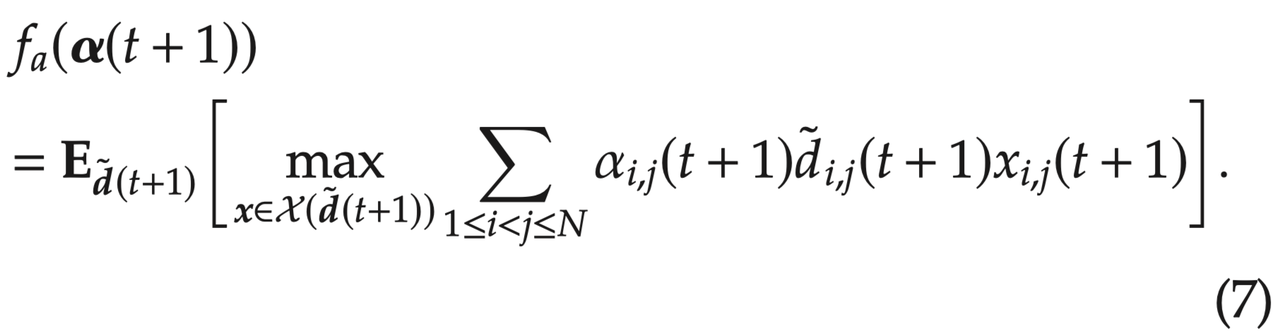
我们可以看到，这个动态规划形式的表达式（7）本质上和模型（2）是一样的。通过DAA策略，填充率目标的可行性问题被分解成一系列标准的动态规划问题。接下来，我们来看DAA策略是怎么应用在算法1里来求解最优流量控制策略的。

1）输入：列车最大客容量$S$，所有起始目的站对需要运输的乘客量的分布函数$\tilde{\mathbf{d}}$，填充率目标${\mathbf{\beta }}^{\prime }$，样本量大小$T$；

2）根据每对起始目的站的$(i,j)$的需求分布，生成独立同分布 (i.i.d.) 的需求样本${\tilde{d}}_{i,j}(1),...,{\tilde{d}}_{i,j}(T)$；

3）基于DAA策略，在需求样本$\tilde{\mathbf{d}}(1),...,\tilde{\mathbf{d}}(T)$上不断求解收益最大化问题(7)，并得到平均债务向量 { α ( t ) } t = 1 T \{{\boldsymbol{\alpha}(t)}\}_{t=1}^{T} {α(t)}t=1T​；

4）从 { 1 , . . . , T } \{1,...,T\} {1,...,T}等比例随机地选取一个周期指数$\overline{t}$，并令$\overline{\mathbf{\alpha }}=\mathbf{\alpha }(\overline{t})$；

5）用得到的系数变量$\overline{\mathbf{\alpha }}$求解收益最大化问题(7)，并返回在策略$\tilde{G}$下所有起始目的站对接受的乘客比例${\mathbf{x}}^{\tilde{G}}(\tilde{\mathbf{d}})$；

6）输出：最优流量控制策略${\mathbf{x}}^{\tilde{G}}(\cdot )$。

文章中的定理2给出了这个随机算法可实现任意填充率目标的理论依据。接下来，论文在满足（3）的前提下进一步改进算法1来最大化收益（2）。通过构造一个最小收益目标$Z$，然后在“债务”向量中引入一个额外的维度来追踪每个样本时段所获得的收益与收益目标$Z$之间的差距，接下来再将改进的收益部分纳入动态规划表达式 (7)中。完善后的算法2可以在原文的附录中找到，定理3为算法2中收益目标和填充率目标的同时可实现性提供了理论支撑。引入了这个收益目标$Z$之后，为了找到在给定填充率目标 $\mathbf{\beta }$ 下可得到的最大收益， 可以先设定一个最大收入目标 $Z_{max}$作为算法 2 的输入， 如果收益目标无法实现，就降低收益目标； 否则，可以不断提高收益目标以获得更高的收益。

三、仿真实验

在仿真实验中，论文在不同的列车容量水平下（100-120）测试DAA策略的性能，并假设每个OD对的需求服从截断正态分布 d i , j ∼ m a x { 0 ; Normal ( d ˉ i , j , ( d ˉ i , j / 3 ) 2 ) } d_{i,j} \sim max\{0; \text{Normal}(\bar{d} _{i,j},(\bar{d}_{i,j}/3)^2)\} di,j​∼max{0;Normal(dˉi,j​,(dˉi,j​/3)2)}，其中${\bar{d}}_{i,j}$表示沿着路线$（i,j）$上的需求均值，之后生成两组样本大小均为$T=5000$的独立同分布OD需求样本（即训练数据和测试数据）。首先使用训练数据首先来求解一个离线优化问题，然后将获得的填充率目标作为在线问题中DAA策略的输入。

论文考虑了收益最大化策略（RMP）和公平性导向策略（FOP）两种情形下的流量控制问题，并分别设置${\beta }_{i,j}=0$与${\beta }_{i,j}={\beta }_{max}$（${\beta }_{max}$表示基于需求样本和列车容量可以提供的最小填充率中的最大值）先来解决离线优化问题。RMP 策略表示在不考虑公平问题的情况下最大载客量，而 FOP策略则在最大化所有OD对的最小填充率的同时优化列车总载客量。然后用得到的填充率${\mathbf{\beta }}^{RMP}$与${\mathbf{\beta }}^{FOP}$来作为在线客流控制问题的输入在测试数据上进行实验。注意这里的${\mathbf{\beta }}^{RMP}$与${\mathbf{\beta }}^{FOP}$都是帕累托最优填充率目标，因此得到的收益也都是最优值。

表2为作者将DAA策略与三个基准策略进行三个维度的性能比较的结果。三个基准策略分别为：(1) 利用测试数据中的实际需求信息，通过经典的样本平均逼近方法，我们将得到的Hindsight（回顾性）最优解作为最优动态规划解的上界；(2) Zhong et al.（2018）提出的响应策略类似于DAA策略，不同之处在于“债务”向量是在获知每个样本的所有需求信息后生成的（完全信息）； (3) 先到先服务 (FCFS) 策略会贪婪地接纳乘客，并且不为下游车站预留运力。三个对比维度分别为：(1) 平均接收的乘客数量，越大越好；(2) 所有OD对填充率的基尼系数，该指标被用于量化服务水平公平性，越大表示交通服务越不公平； (3) 实现的填充率向量与目标填充率之间的欧氏距离，越小越好。为了便于比较，我们将从Hindsight最优解中获得的填充率作为三种策略下的共同填充率目标。

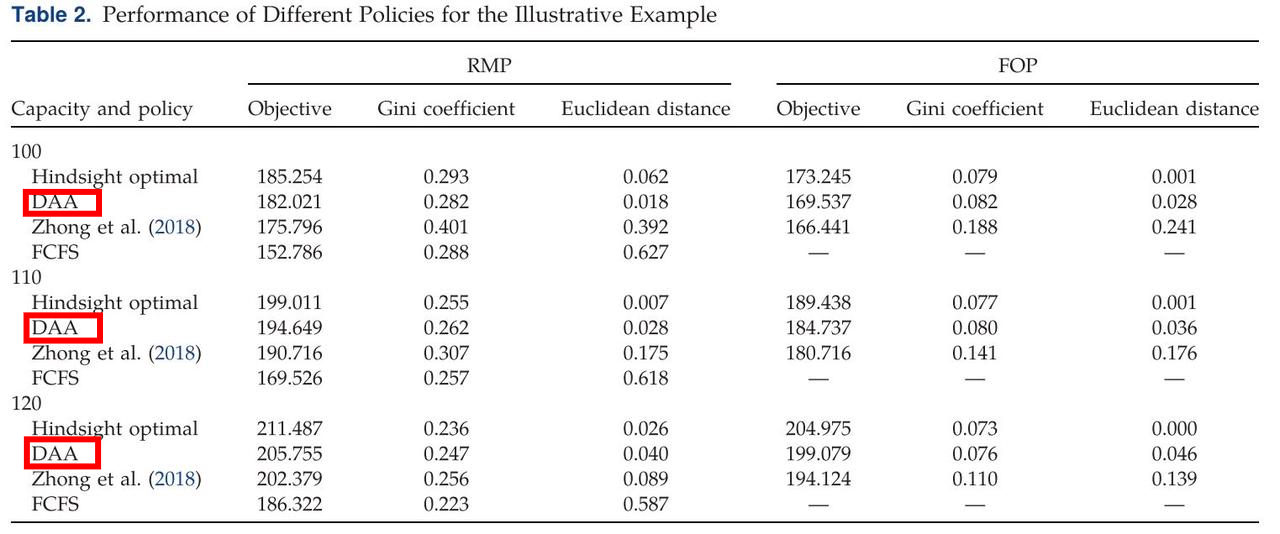
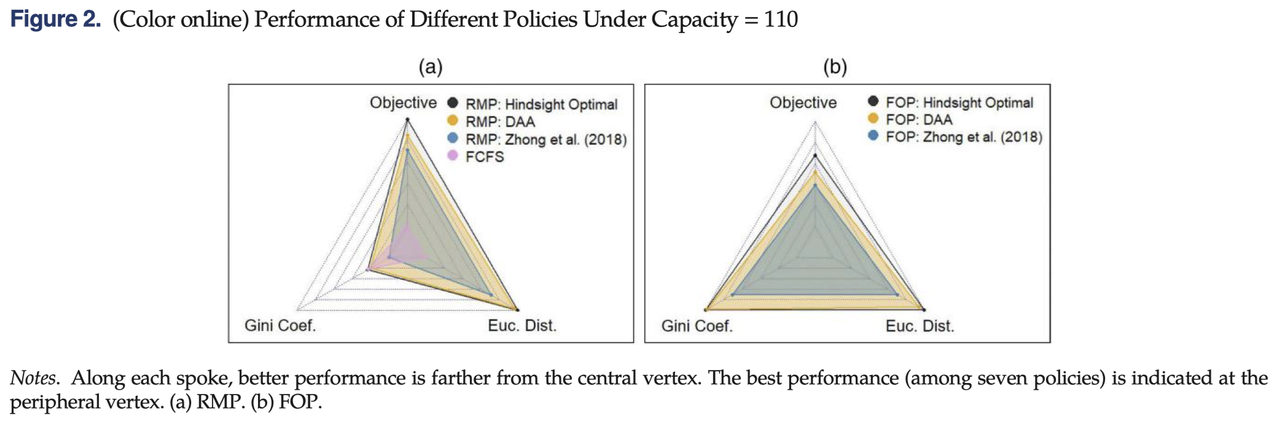
如表2所示，对于任意一种情况，DAA策略与Hindsight最优解之间的差距始终不超过2.71%，这表明了DAA策略是非常有效的，并且得到的结果非常接近最优解。而在Zhong et al.（2018）提出的策略下，无论是在RMP案例还是FOP案例中，欧氏距离都远高于我们的DAA策略，由此我们可以看到正确定义“债务”向量在解决（OPFCwF）问题中的重要性。更直观一点看，下图2展示了不同策略在列车容量为110时的性能对比图，我们可以看到在RMP和FOP两种案例中，本文提出的DAA策略都在各个维度上都明显优于Zhong et al.（2018）策略。对比FCFS策略，从左边的（a）图中可以看到，除了在基尼系数一栏上具有可以忽略的微弱差距（1%），我们的DAA在其他维度上也都表现出明显更优的结果。

文章也基于北京市地铁的真实数据进行了仿真实验，并得到了一致的结论。

四、小结​

在本文中，作者提出了一类新型的客流控制策略来解决公共交通系统的客流过饱和问题，在最大化承载量的同时确保每个OD的服务水平公平性。作者利用 Blackwell’s approachability theorem 和 Fenchel duality简化了分析，提出了一种用来求解具有服务水平约束随机动态规划问题的方法，数值实验结果表明这个方法在实际应用中具有良好的性能。

参考文献

[1] Liang, J., Lyu, G., Teo, C. P., & Gao, Z. (2023). Online Passenger Flow Control in Metro Lines. Operations Research.

[2] Zhong Y, Zheng Z, Chou MC, Teo C-P (2018) Resource pooling and allocation policies to deliver differentiated service. Management Sci. 64(4):1555–1573.