GELU激活函数: 高斯误差线性单元

本文主要是介绍GELU激活函数: 高斯误差线性单元，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

【Reference】
1. GAUSSIAN ERROR LINEAR UNITS (GELUS)

---

引言

早期网络使用二元阈值单元，sigmoid激活函数将二元阈值决策平滑，使得神经元可解释为发射率，并得以通过BP算法训练。随着网络深度增加，在训练神经网络时，sigmoid激活函数已被证实不如一些非平滑的非线性激活函数高效，如ReLU通常比sigmoid训练更快、收敛更快，ELUs允许ReLU输出负值，通常能够进一步加快训练速度。

深度非线性网络可以很好地拟合数据，因此设计者常向网络引入随机正则化，如隐藏层中添加噪声、应用dropout等，这些正则化操作与输入函数不同。某些随机正则化如dropout，使得网络能够近似于多个网络的集成（集成模型能够显著增加准确率）。正则化与非线性激活函数共同决定网络输出，正则化用于辅助非线性激活函数。

本文提出一种新的非线性激活函数Gaussian Error Linear Unit (GELU)，它是自适应dropout修正的期望，与随机正则化有关。GELU使得神经元输出具有概率性。GELU在多数CV、NLP、ASR等领域表现出比ReLU、ELUs更优异的性能。

GELU公式

我们结合dropout、zoneout和RELUs的一些性质构造激活函数，对于同时使用RELUs和dropout的网络，RELUs将输入乘以1或0，而dropout将输入随机乘以0。新的RNN正则化器zoneout，随机将输入乘以1。我们通过随机向输入乘以1或0，合并这些性质，这些zero-one mask随机确定，但依赖于输入。

具体地说，我们使用$m\sim \text{Bernoulli}(\Phi (x))$乘以神经元输入，其中$\Phi (x)=P(X\le x)$，$X\sim \mathcal{N}(0,1)$是标准正太分布的累计分布函数。选择这一分布的原因是因为输入特征多服从于正太分布，比如使用Batch Norm的网络。这一条件下，随着输入$x$的降低，其被drop的概率逐渐增加，这种对输入$x$的转换是随机的、且依赖于自身值。

这种非线性变换可看作随机正则化器对输入$x$的期望：
$$x\Phi (x)=\Phi (x)\times Ix+(1-\Phi (x))\times 0x$$
不严谨地说，该表达式表示根据$x$比其他输入大多少对$x$进行缩放。由于高斯累计分布函数常用于计算误差函数，因此我们定义GELUs为
$$\text{GELU}(x)=xP(x\le X)=x\Phi (x)=x\cdot \frac{1}{2}\left[1+\text{erf}(x/\sqrt{2})\right]$$

公式推导

标准正太分布函数$\Phi (x)$和右尾函数$Q(x)$：
$$\Phi (x)=P(X\le x)=\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^x{e}^{-x^2/2}\text{d}x=1-Q(x)$$
误差函数$\text{erf}(x)$：
$$\text{erf}(x)=1-2Q(\sqrt{2}x)=\frac{2}{\sqrt{\pi }}{\int }_0^x{e}^{-x^2}\text{d}x$$
因此
$$\Phi (x)=\frac{1}{2}\left[1+\text{erf}(x/\sqrt{2})\right]$$

近似形式为
$$0.5x(1+\tanh [\sqrt{2/\pi }(x+0.044715x^3)])orx\sigma (1.702x)$$

GELU实验

MNIST CLASSIFICATION

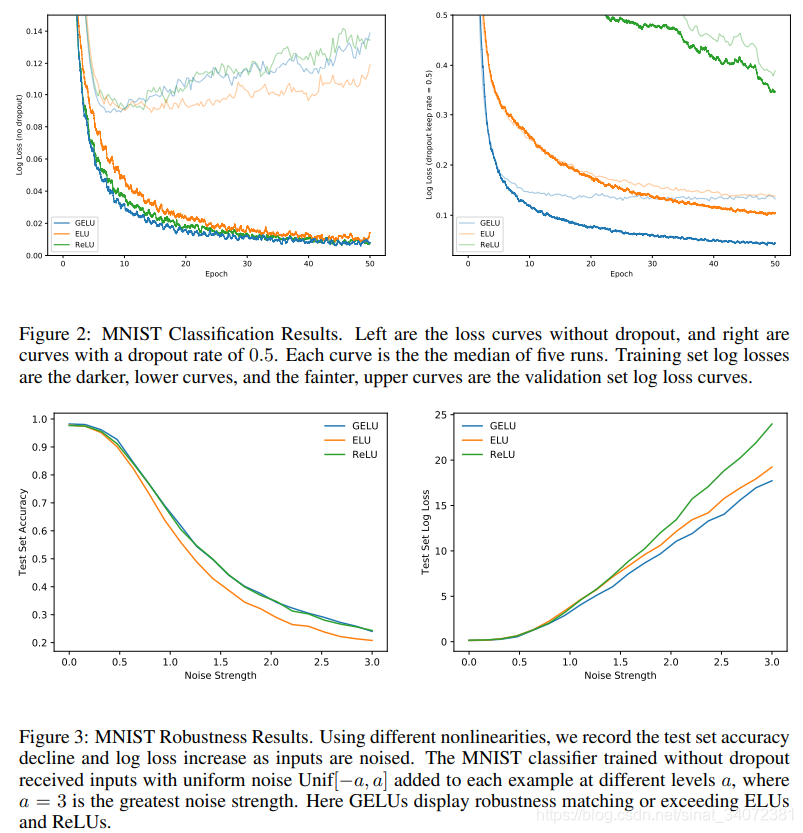
MNIST AUTOENCODER

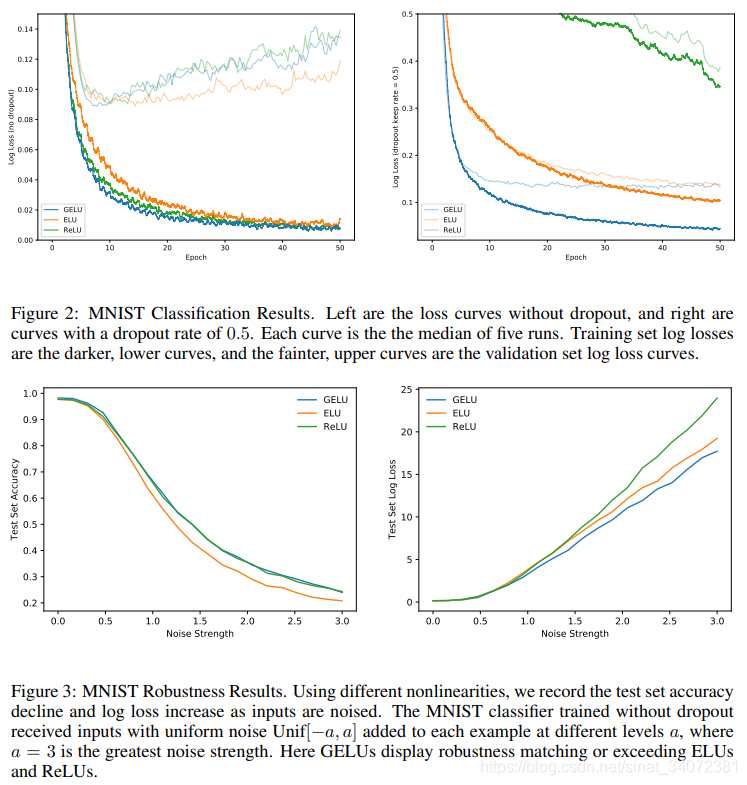
CIFAR-10/100 CLASSIFICATION

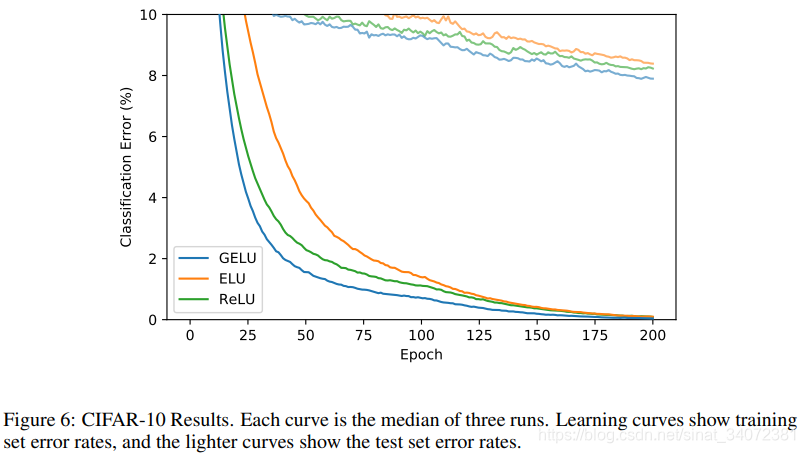
这篇关于GELU激活函数: 高斯误差线性单元的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---