本文主要是介绍[THUPC 2024 初赛] 二进制 (树状数组单点删除+单点查询)(双堆模拟set),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!


题解
题目本身不难想
首先注意到所有查询的序列长度都是小于logn级别的
我们可以枚举序列长度len,然后用类似滑动窗口的方法,一次性预处理出每种字串的所有出现位置,也就是开N个set去维护所有的位置。预处理会进行O(logn)轮,每次需要O(n*logn)的时间复杂度初始化set并计算位置。总共复杂度O(nlog^2n),看一下时间限制6s,感觉可以过23333。
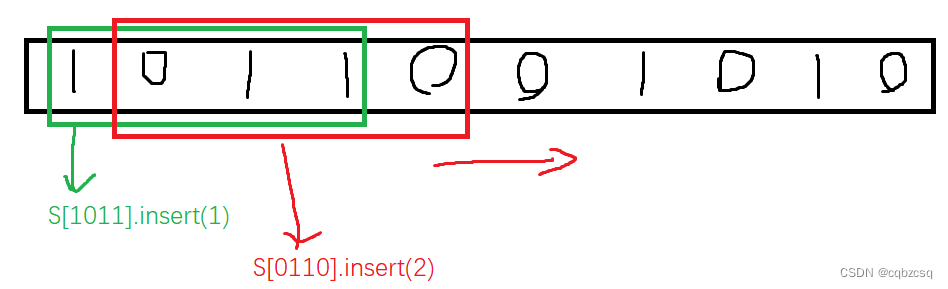
删除操作可以直接暴力,直接从每种字串的位置集合中删除所有被影响到的位置,然后再把删除后字符串合并产生的新的子串加入到set中,过程中需要支持O(logn)的单点删除和单点查询。
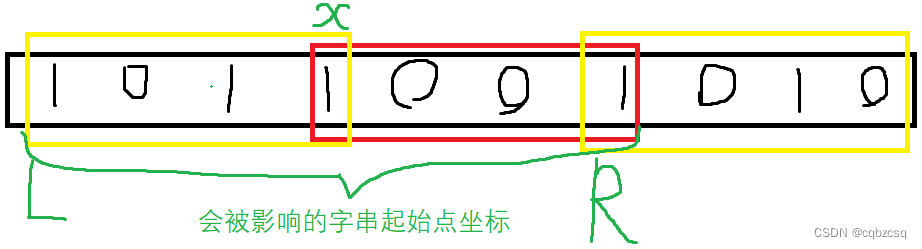
在set中,删除起始点在L~R之间子串信息,再插入起始点在L到x-1的新构成的子串的信息
删除操作最多O(n/logn)次,每次直接暴力就是O(log^2n),总共复杂度O(nlogn)
接下来就是一些小问题,如何维护单点删除、单点查询的序列呢?
首先我们肯定不会去真正的移动序列,保留原始的输入01序列
可以想到用set去维护当前存在的每个坐标,但是支持查询第k个坐标的话得手写平衡树
也可以想到用线段树或者树状数组维护每个位置的存在信息,在线段树或者树状数组上二分来查询删除后的序列中的第k个坐标的真实位置。

这里使用树状数组
树状数组二分类似于倍增查询LCA的思想,十分易懂。
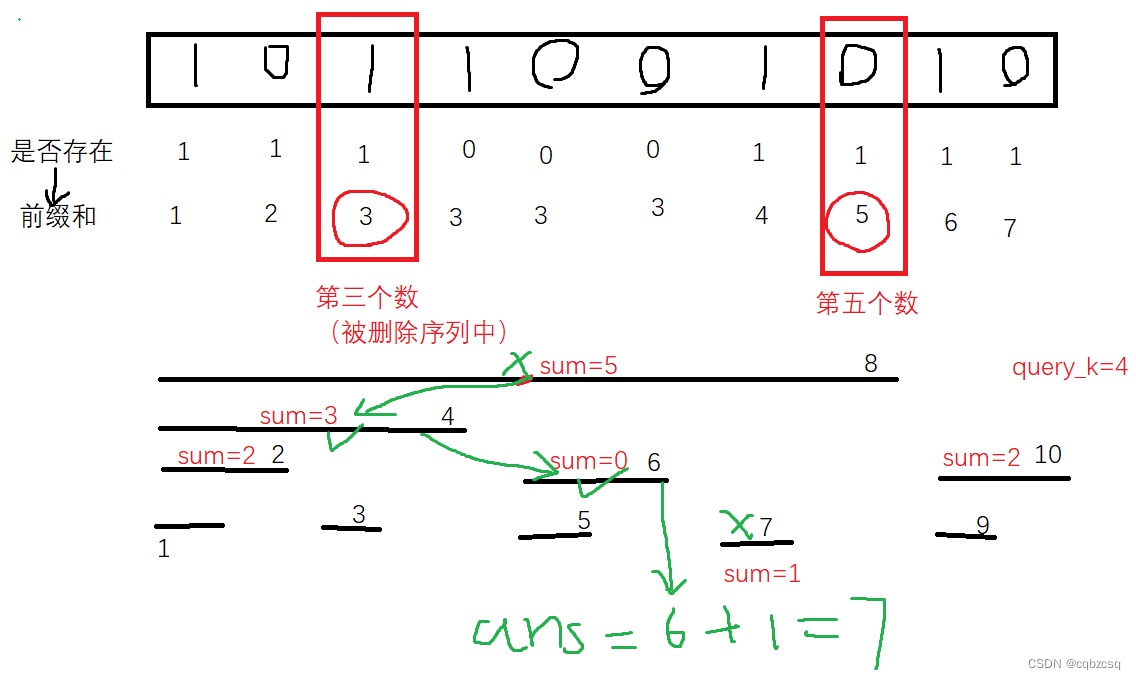
然后我们迅速写完整个内容,交一发,发现TLE了
看一下复杂度,发现瓶颈在于预处理,于是我们把初始化中对每个位置都进行树状数组二分,替换为直接使用当前位置存在信息数组进行处理,这样预处理中计算坐标的部分就变成O(n)了
但是仍然TLE了
现在瓶颈仍然是预处理,如果C++支持对有序序列O(n)建立set就好了
后来看了洛谷上题解的方法,才知道可以用两个优先队列来模拟set
由于我们只需要维护集合中的最小值以及集合的元素个数
使用两个堆,一个维护插入的内容,另一个维护删除的内容
当查询个数时,两个堆的大小相减即可。当查询最小值时,如果“删除堆”中的最小值与“插入堆”中的最小值相等,就两个一起pop掉,直到找到第一个“插入堆”中存在,但“删除堆”中不存在的元素即可。
(其实也可以用两个vector来模拟,因为对于每种子串,查询的次数只有一次,所以可以大胆排序再查询,这样初始化时间复杂度也是O(nlogn),查询删除子串的总时间复杂度是最坏O(nlog^2n)不过似乎也能过,因为sort在大部分都有序的情况下还是很快的)
改完之后,从6.18s变成了1.17s,发生了质的飞跃23333
有人可能会问,优先队列插入不也是O(logn)的吗,为什么会比set快这么多,因为预处理的过程中插入集合的内容是顺序的,根据小根堆的实现,只有当自己比父亲值小时,才会发生交换,所以在预处理建立小根堆的过程中是O(n)的,这样预处理的总复杂度就变成了O(nlogn),删除方面在理论上最坏时间复杂度也是O(nlog^2n)(假设所有的位置都集中在一种子串上,并且“删除堆”和“插入堆”差不多大)
代码:
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<set>
#include<queue>
using namespace std;
#define N 1000005
#define LOG 20
int n, n_real, now;
char ss[N];
// 树状数组维护单点删除与单点查询的序列
// 实际坐标->逻辑坐标(删除后的坐标) getsum
// 逻辑坐标->实际坐标 query 树状数组二分
int tra[N];
int getsum(int x)
{int ret=0;for(;x;x-=x&-x) ret+=tra[x];return ret;
}
void update(int x,int k)
{for(;x<=n;x+=x&-x)tra[x]+=k;
}
int query(int k)// 查询删除后序列的第k位置的实际坐标
{int ans=0,sum=0;for(int i=LOG;i>=0;i--){if(ans+(1<<i)<=n && sum+tra[ans+(1<<i)]<k){sum+=tra[ans+(1<<i)];ans+=(1<<i);}}return ans+1;
}
// a是原始数据,tmp是删除后的数组,b表示当前位是否存在(树状数组建立在b上)
bool a[N],tmp[N],b[N];
int pos[N];
void cal_tmp_all()
{int cnt=0;for(int i=1;i<=n;i++){if(b[i]){pos[++cnt]=i;tmp[cnt]=a[i];}}
}
void cal_tmp(int l,int r)
{l=max(1,l);r=min(r,n_real);for(int i=l;i<=r;i++){pos[i]=query(i);tmp[i]=a[pos[i]];}
}
priority_queue<int,vector<int>,greater<int> > S[N],D[N];
//set<int> S[N];
//set<int>::iterator it;
// 将起始点在l r之间,长度为len的数据加入到set或者从set中删除
void update_set(int l,int r,int len,bool flg)
{r=min(n_real,r+len-1);int lim_l= max(now,1<<(len-1)), lim_r= min(n,(1<<len)-1);int mask=(1<<len)-1;int tmp_value=0;for(int i=l;i<=r;i++){tmp_value=((tmp_value<<1)&mask)|tmp[i];if(i-l+1 >= len && tmp_value>=lim_l && tmp_value<=lim_r){if(flg)S[tmp_value].push(pos[i-len+1]);elseD[tmp_value].push(pos[i-len+1]);}}
}
int main()
{scanf("%d",&n);n_real=n;scanf("%s",ss+1);for(int i=1;i<=n;i++){a[i]=int(ss[i]-'0');update(i,1);b[i]=1;}now=1;for(int len=1;n>>(len-1);len++){cal_tmp_all();update_set(1,n_real,len,1);//printf("start len:%d\n",len);for(;now<(1<<len);now++){//printf("now:%d\n",now);if(now>n)return 0;int siz = (int)S[now].size()-(int)D[now].size();if(!siz){printf("-1 0\n");continue;}while(!S[now].empty()&&!D[now].empty() && S[now].top()==D[now].top()){S[now].pop();D[now].pop();}int x=getsum(S[now].top());printf("%d %d\n",x,siz);int l=max(1,x-len+1),r=min(n_real,x+len-1);// 删除受影响的结果cal_tmp(l,r+len-1);update_set(l,r,len,0);// 删除对应的01序列for(int i=x;i<=r;i++){update(pos[i],-1);b[pos[i]]=0;}n_real-=len;// 添加新产生的序列结果cal_tmp(l,x-1+len-1);update_set(l,x-1,len,1);while(!S[now].empty())S[now].pop();while(!D[now].empty())D[now].pop();}}
}这篇关于[THUPC 2024 初赛] 二进制 (树状数组单点删除+单点查询)(双堆模拟set)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




