GAN笔记_李弘毅教程(六)WGAN、EBGAN

本文主要是介绍GAN笔记_李弘毅教程(六)WGAN、EBGAN，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在大多数情况下， $P_G$和 $P_{data}$训练到最后是不会重叠的。因为有两点。
1.data本质： $P_G$和 $P_{data}$是高维空间中的低维合成，这个重叠几乎是可以忽略的。（开始训练时）
2.从Sample角度来说，Sample两个部分，这两个部分交叠的部分也比较少。

当 $P_G$和 $P_{data}$没有重叠的时候，用JS散度看它们之间的差异会在train的过程造成很大的障碍。
完全不重叠时，JS divergence=log2,下图最后一张图表示完全重叠。
下图表示，一开始不重叠时，JS divergence=log2,虽然第二张图距离近些，但仍是JS divergence=log2，而且第一张图因为JS divergence等于常数就无法迭代到第二张图。更无法迭代到第三张图。
当两者没有重叠时，二维分类器就可以完全辨别出这两者，最后的出来的目标函数值也会是相同的。

当很平的时候，就迭代不了了。（有点像梯度消失）
解决方法：LSGAN就是把sigmod换成linear。
positive值越接近1越好，negtive值越接近0越好。

Wasserstein GAN(WGAN)

把P这抔土移到Q的平均距离，如果P到Q的distance恒为d,那么Earth Mover’s Distance为1。

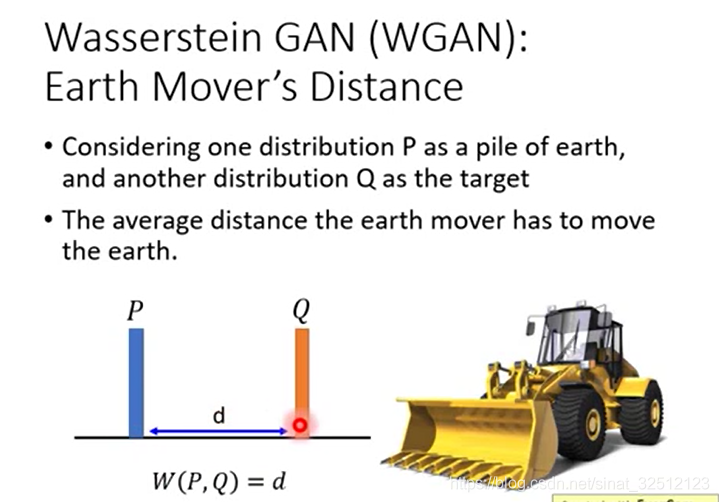
但当不恒定的时候，要使两者分布相同，可以有不同的方法。但哪一种才是所需要的？
穷举出每个方法所需要的距离，最小的即为最优。


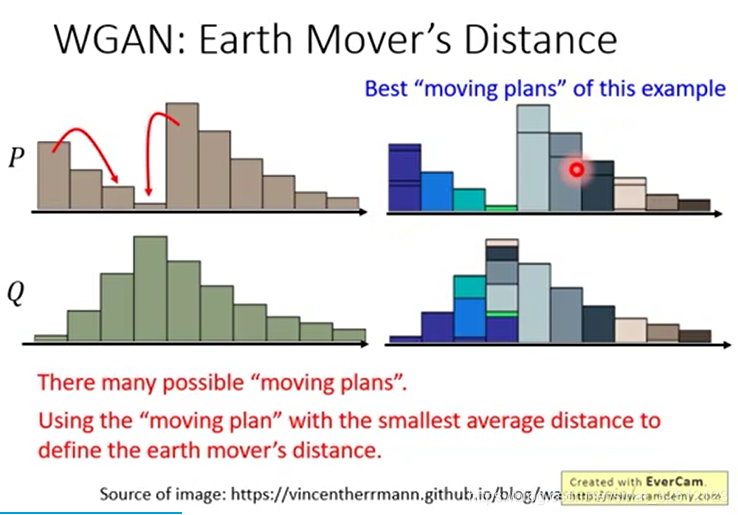
更正规的表达方式如下图
每一个方块表示要把对应的P拿多少移到对应的Q，越亮表示移动越多。
（为什么一行或一排合起来就是高度？）
$\gamma (x_p,x_q)$表示要从$x_p$拿多少$x_q$，$||x_p-x_q||$表示两者间距离
穷举$\gamma$,看哪个$\gamma$让$W(P,Q)$最小，这个最小的距离$W(P,Q)$即为the best plan

右上角是眼睛的进化过程。下图可以把JS散度过程转为WGAN过程，因此可以迭代成功。

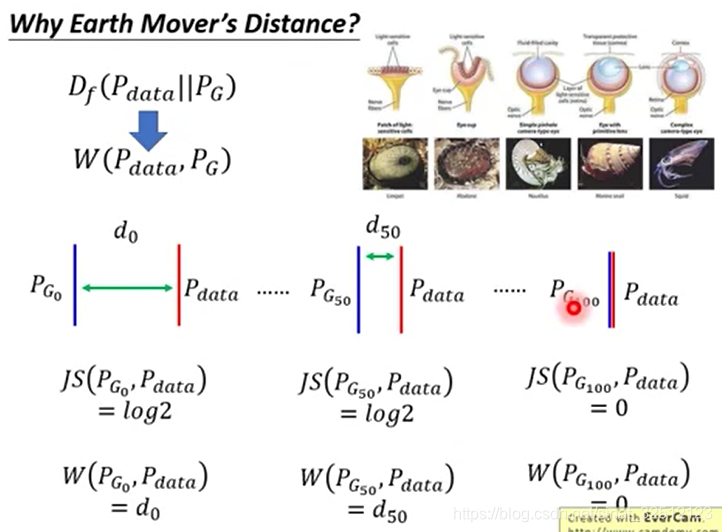
如何设计D，就可用WGAN?
Lipshitz表示D是很平滑的意思。
如果只是一味的让real越来越大，generated越来越小。系统会崩溃。因此需要设置额外的限制。
这个限制就是D必须是平滑的。

Lipshitz函数的定义如下图
output差距不能比input差距大
k=1时，即为1-Lipshitz。
绿色的线是1-Lipshitz。

怎么解？
最原始的方法就是Weight Clipping
设置最大最小值

但是WGAN只是单纯的smooth,因此衍生出一个Improved WGAN(WGAN GP)

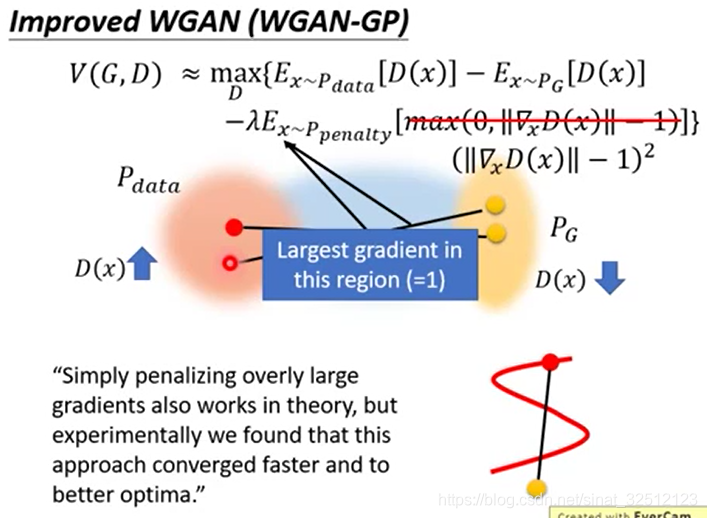
Improved WGAN(WGAN GP)

加一个修正项，但无法check无论是哪一个x都满足小于等于1这个条件，所以把x从概率分布为$P_{penalty}$的x中sample出来的。其他范围内的管不了

$P_{penalty}$就是下图中蓝色的从$P_{data}$到$P_G$的距离范围。
实验证明这样做ok。
理论上也是因为要从$P_G$搬到$P_{data}$，所以中间的蓝色区域才影响结果，其他地方的无所谓。

实际上，$||{\nabla }_{x}D(x)||$越接近1越好，无论大于1还是小于1，都要有惩罚。

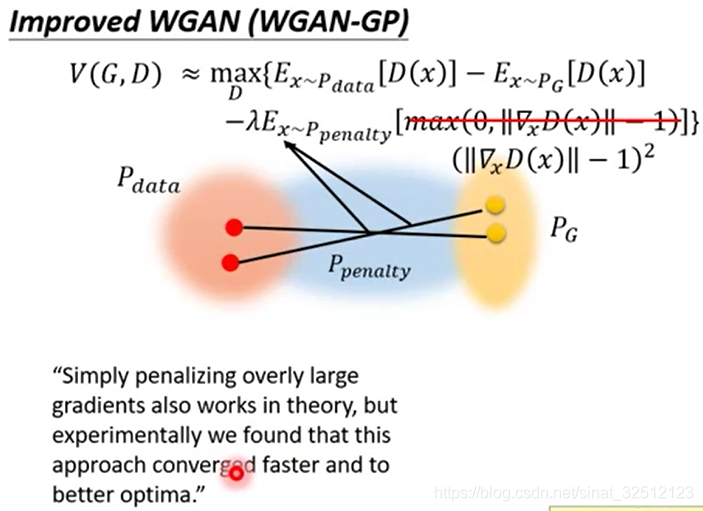
Improved WGAN(WGAN GP)也存在一些问题
有人提出要把$P_{penalty}$放到$P_{data}$里。

也可以用Spectrum Norm(频谱范数？)
能让每一个梯度范数都小于1

以下是原始GAN的算法

而WGAN改变的地方如下
去掉sigmoid，让输出是linear的。
加上Weight clipping,来使结果收敛。

Energy-based GAN(EBGAN)

BEGAN是它的变形。
改了D的架构，本来D是二维分类器架构，但EBGAN将其变为一个autoencoder；G不变。
D输出的也是scalar，scalar是从autoencoder出来的。
好处就是这个autoencoder可以在没有G的情况下用真实值就被预训练。
用原来的方法，刚开始D不会很厉害的。用EBGAN一开始就可以产生比较厉害的D。

建设是难得，破坏是容易的。
D中negative样本对应的值小于一个值就行

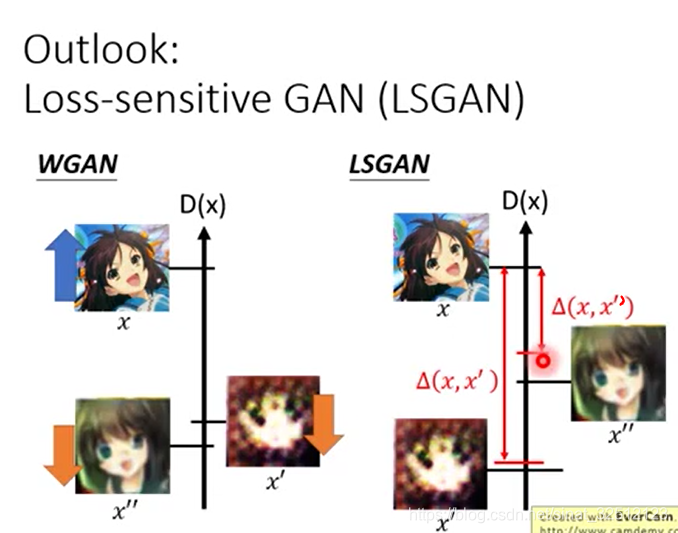
Loss-sensitive GAN(LSGAN)

当已经有相对比较逼真的图片时，那就不要把它压得很低，放到上面点的位置。

这篇关于GAN笔记_李弘毅教程(六)WGAN、EBGAN的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---