电机气隙磁密FFT分析处理

1. 模型

基于Halbach直线电机的永磁体磁化方向如下图所示，

2. FFT by Maxwell

由Maxwell得到的一对磁极下气隙的磁密度波形如下图所示，

通过Maxwell的FFT得到傅里叶分解如下图所示，

3. FFT by python & Matplotlib (Recommended)

将气隙磁密度（Bx）导出为csv格式，Python中的FFT代码如下，

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.pylab import mplmpl.rcParams['font.sans-serif'] = ['SimSun']
mpl.rcParams['axes.unicode_minus']=False
#plt.rcParams['figure.dpi'] = 300
plt.rcParams['figure.constrained_layout.use'] = Truefig = plt.figure()
fixed_width_mm = 340
fixed_height_mm = 170
fixed_width_inch = fixed_width_mm / 25.4
fixed_height_inch = fixed_height_mm / 25.4
fig.set_size_inches(fixed_width_inch, fixed_height_inch)ax1 = fig.add_subplot(121)
ax2 = fig.add_subplot(122)data = pd.read_csv('Bx.csv')
x = data['Distance [mm]']
y = data['bx []']
ax1.plot(x,y,color='r',label='orgin',ls='--')fft_y=np.fft.fft(y)
N=fft_y.shape[0]orders=11
order=orders+1fundamental=np.abs(fft_y[1])/N*2
harmonics=np.abs(fft_y[2:order])/N*2
thd=np.sqrt(np.sum(harmonics**2))/fundamental
thd_per = round(thd*100, 2)for i in range(order):new_fft_y=np.zeros_like(fft_y)new_fft_y[i]=fft_y[i]ifft_y=np.fft.ifft(new_fft_y).real*2ax1.plot(x,ifft_y,label='order='+str(i))normalization_y=np.abs([fft_y[i]])/N*2ax2.bar(i,normalization_y)ax1.legend()
ax1.set_title('各次谐波分解示意图')
ax1.set_xlabel('长度(mm)')
ax1.set_ylabel('各次谐波幅值大小')
ax1.set_xlim(x[0],x[len(x)-1])ax2.set_title('各次谐波FFT分解柱状图 (THD='+str(thd_per)+'%)')
ax2.set_xlabel('谐波次数')
ax2.set_ylabel('各次谐波幅值大小')
ax2.set_xlim(0,order)
ax2.set_xticks(np.arange(0,order,1))plt.show()

  FFT 如下：

4. FFT by Matlab (Not recommended)

将气隙磁密度（Bx）导出为csv格式，matlab中的FFT代码如下，

clc
clear all;
format long;
Ns=1001;		%采样点
order=11;		%谐波数
filename='Bx.csv';		%导出的气隙磁密数据集
data=csvread(filename,1,0);     %从行偏移量 R1 和列偏移量 C1 开始读取文件中的数据
x=data(:,1);        %取第一列
y=data(:,2);        %取第二列
figure;
plot(x,y,'r');      %plot origional waveform
hold on;
grid on;
fft1=fft(y,Ns);
j=0;
amp_har=zeros(1,(order));
%%
for m=1:1:order
j=j+1;
fft1=fft(y,Ns);
fund_ele_front=fft1(m+1);
fund_ele_back=fft1(Ns+1-m);
amp_har(j)=(abs(fund_ele_front))/Ns*2;
fft1=0*fft1;
fft1(m+1)=fund_ele_front;
fft1(Ns+1-m)=fund_ele_back;
fft1=ifft(fft1,Ns);
fft1=real(fft1);
plot(x,fft1);
title('各次谐波分解示意图')
xlabel('长度(mm)')
ylabel('各次谐波幅值大小')
hold on;
end
%%
k=(1:1:order);
figure;
bar(k,amp_har);
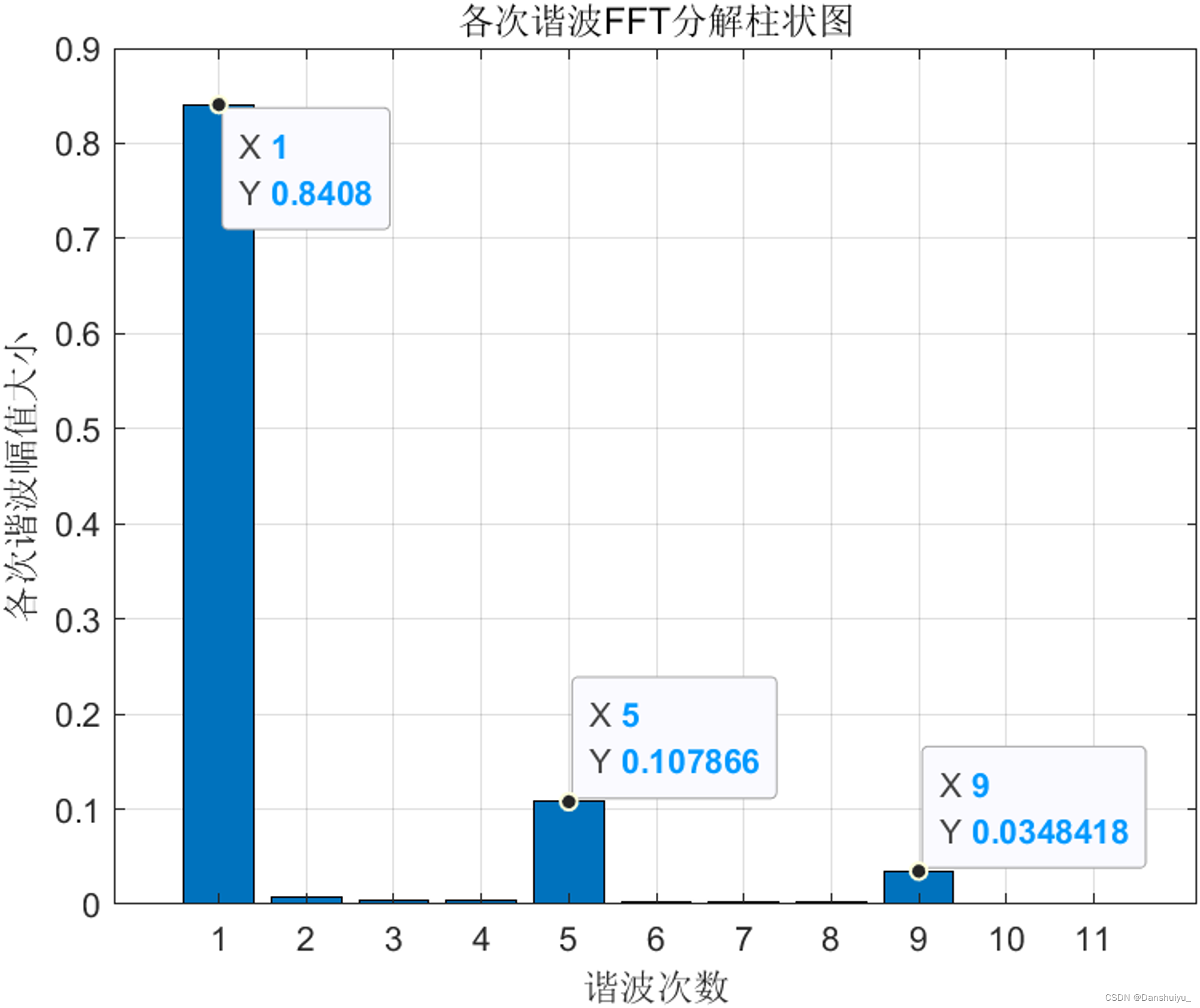
title('各次谐波FFT分解柱状图')
xlabel('谐波次数')
ylabel('各次谐波幅值大小')
grid on;
peak_b=max(fft1);
rms_b=0.707*peak_b;
s=amp_har.^2;
THD = sqrt(sum(s(2:(order+1)/2)))/(amp_har(1));
THD_pct = 100*THD;

各谐波的分解如下：

各谐波FFT分解直方图如下：

About Project

• Version：ANASYS Electronics Suite 2021 R2
• Source Code: Github or Gitee