有限元法计算二维圆柱绕流问题——Python代码实现

一、问题描述

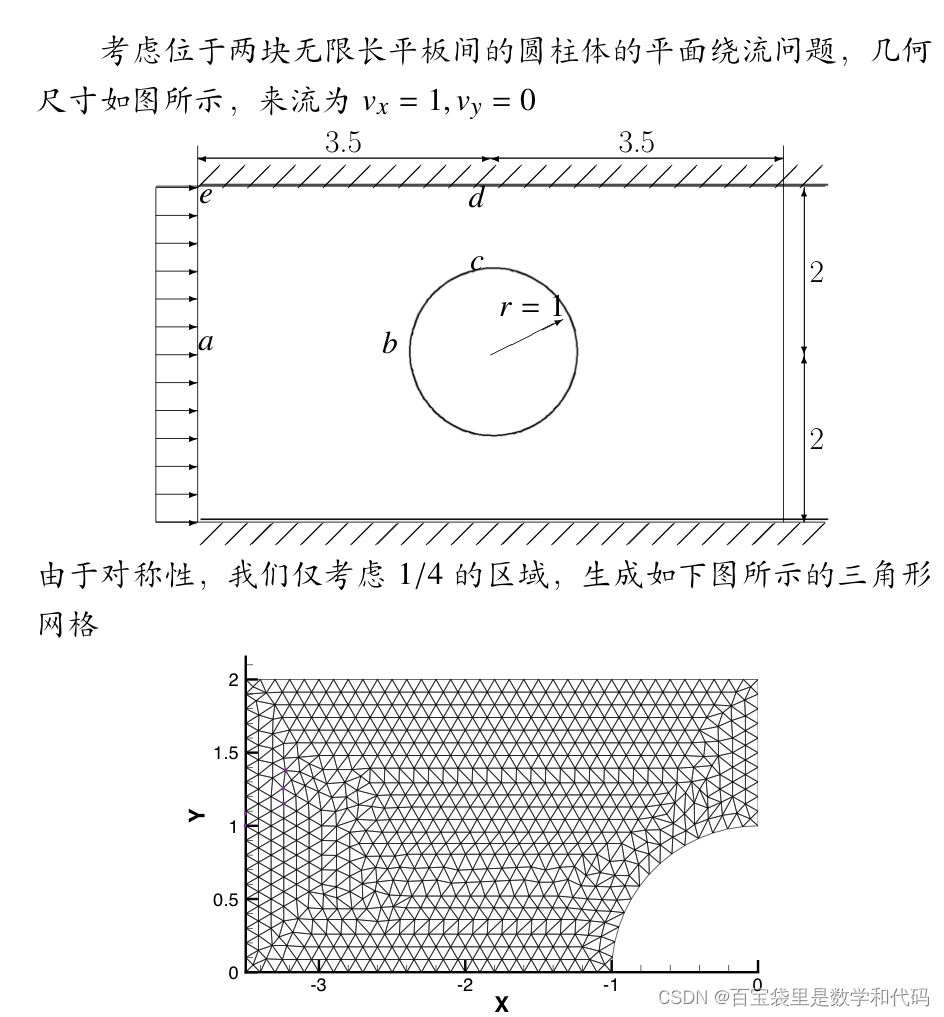
选取流函数Ψ为变量，对拉普拉斯方程进行求解（右边界为自然边界条件，其余边界为本质边界条件）；

网格数据文件的生成暂时不在本文中详述。

二、节点和单元的数据读取

import numpy as np
import matplotlib as plt
from mpl_toolkits.mplot3d import Axes3D# 打开文件
try:with open('grid.dat', 'r') as f:# 读取节点数NP和单元数NEline = f.readline().strip()NP, NE = map(int, line.split())# 读取节点坐标X[0:NP,0]和X[0:NP,1]X = np.zeros((NP, 2),dtype = float)for i in range(NP):line = f.readline().strip()X[i] = np.array(list(map(float, line.split())))# 读取单元节点对应关系数组NOD[0:NE,0:3]NOD = np.zeros((NE,3),dtype = int)for i in range(NE):line = f.readline().strip()NOD[i] = np.array(list(map(int, line.split())))-1 #注意文件里的索引是从1开始的，而节点坐标数组X是从0开始的except FileNotFoundError:print("文件不存在")
except Exception as e:print("文件读取失败：", e)

三、设置本质边界条件

#设置本质边界条件
Ψ = np.zeros(NP)
substantial_bound_index = []
unknown_index = []
for i in range(NP):if X[i,1] == 0 :Ψ[i] = 0substantial_bound_index.append(i)elif X[i,1] == 2:Ψ[i] = 2substantial_bound_index.append(i)elif X[i,0] == -3.5:Ψ[i] = X[i,1]substantial_bound_index.append(i)elif abs(X[i,0]**2 + X[i,1]**2 - 1)<= 1e-3:#如果网格尺度变化，此处可能需要调整Ψ[i] =  0substantial_bound_index.append(i)else:unknown_index.append(i)

四、计算单元方程和整体方程

A_overall = np.zeros((NP,NP)) #整体方程的系数矩阵
f_overall = np.zeros(NP) #整体方程的右端项
#遍历所有单元，求单元方程的系数矩阵，并累加到整体方程的系数矩阵上
for i in range(NE):X_i = np.zeros(3)Y_i = np.zeros(3)node_index = np.zeros(3)node_index = NOD[i,:] #是从0开始的X_i = X[node_index,0]Y_i = X[node_index,1]A = 0.5*((X_i[1]-X_i[0])*(Y_i[2]-Y_i[0])-(Y_i[1]-Y_i[0])*(X_i[2]-X_i[0]))b1 = (Y_i[1]-Y_i[2])/(2*A)b2 = (Y_i[2]-Y_i[0])/(2*A)b3 = (Y_i[0]-Y_i[1])/(2*A)c1 = -(X_i[1]-X_i[2])/(2*A)c2 = -(X_i[2]-X_i[0])/(2*A)c3 = -(X_i[0]-X_i[1])/(2*A)A_overall[node_index[0],node_index[0]] += b1*b1 + c1*c1A_overall[node_index[1],node_index[1]] += b2*b2 + c2*c2A_overall[node_index[2],node_index[2]] += b3*b3 + c3*c3A_overall[node_index[0],node_index[1]] += b1*b2+c1*c2A_overall[node_index[1],node_index[0]] += b1*b2+c1*c2A_overall[node_index[0],node_index[2]] += b1*b3+c1*c3A_overall[node_index[2],node_index[0]] += b1*b3+c1*c3A_overall[node_index[1],node_index[2]] += b2*b3+c2*c3A_overall[node_index[2],node_index[1]] += b2*b3+c2*c3

#代入本质边界条件上的函数值，消元，只剩下待求节点的函数值
#计算消元后待求节点对应的右端项
for i in unknown_index:sum = 0for j in substantial_bound_index:sum += (-1)*A_overall[i,j]* Ψ[j]f_overall[i] = sum

#解线性方程组
A_tosolve = np.zeros((len(unknown_index),len(unknown_index)))
A_tosolve = A_overall[np.ix_(unknown_index,unknown_index)]
f_tosolve = f_overall[np.ix_(unknown_index)]
sol = np.linalg.solve(A_tosolve, f_tosolve)

#得到完整的节点Ψ数组
pos = 0
for i in unknown_index:Ψ[i] = sol[pos]pos+=1

五、计算单元和节点的流速和压强分布

首先利用前面计算出的节点流函数值，插值得到每个单元的流速；

然后，每个节点的流速则用相邻单元流速的加权平均（以单元面积为权重）得到；

最后，通过伯努利方程计算出节点的压强。

#计算单元的速度
vx = np.zeros(NE)
vy = np.zeros(NE)#计算节点的速度——每个节点的速度采用相邻单元速度的面积加权平均
node_sum_area = np.zeros(NP) #每个节点相邻的累积面积
vx_node = np.zeros(NP)
vy_node = np.zeros(NP)#遍历所有单元
for i in range(NE):X_i = np.zeros(3)Y_i = np.zeros(3)node_index = np.zeros(3)node_index = NOD[i,:] #是从0开始X_i = X[node_index,0]Y_i = X[node_index,1]A = 0.5*((X_i[1]-X_i[0])*(Y_i[2]-Y_i[0])-(Y_i[1]-Y_i[0])*(X_i[2]-X_i[0]))b1 = (Y_i[1]-Y_i[2])/(2*A)b2 = (Y_i[2]-Y_i[0])/(2*A)b3 = (Y_i[0]-Y_i[1])/(2*A)c1 = -(X_i[1]-X_i[2])/(2*A)c2 = -(X_i[2]-X_i[0])/(2*A)c3 = -(X_i[0]-X_i[1])/(2*A)vx[i] = c1*Ψ[NOD[i,0]]+c2*Ψ[NOD[i,1]]+c3*Ψ[NOD[i,2]]vy[i] = -b1*Ψ[NOD[i,0]]-b2*Ψ[NOD[i,1]]-b3*Ψ[NOD[i,2]]#更新节点的速度均值for j in range(3):s0 = node_sum_area[NOD[i,j]]vx0 = vx_node[NOD[i,j]]vx_node[NOD[i,j]] = (s0*vx0+A*vx[i])/(s0+A)vy0 = vy_node[NOD[i,j]]vy_node[NOD[i,j]] = (s0*vy0+A*vy[i])/(s0+A)node_sum_area[NOD[i,j]]+= A#计算节点的压力
p_node = np.zeros(NP)
for i in range(NP):p_node[i] = 0.5*(1-vx_node[i]**2 - vy_node[i]**2)

六、计算结果

一、流函数数值解的3D图

from mpl_toolkits.mplot3d import Axes3D
from matplotlib.tri import Triangulationtri = Triangulation(X[:, 0], X[:, 1])
#一、绘制流函数数值解的3D图
fig = plt.pyplot.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_trisurf(X[:, 0], X[:, 1], Ψ, triangles=tri.triangles, cmap='viridis',alpha = 0.9)
ax.set_title('Ψ_num')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('Ψ')
plt.pyplot.show()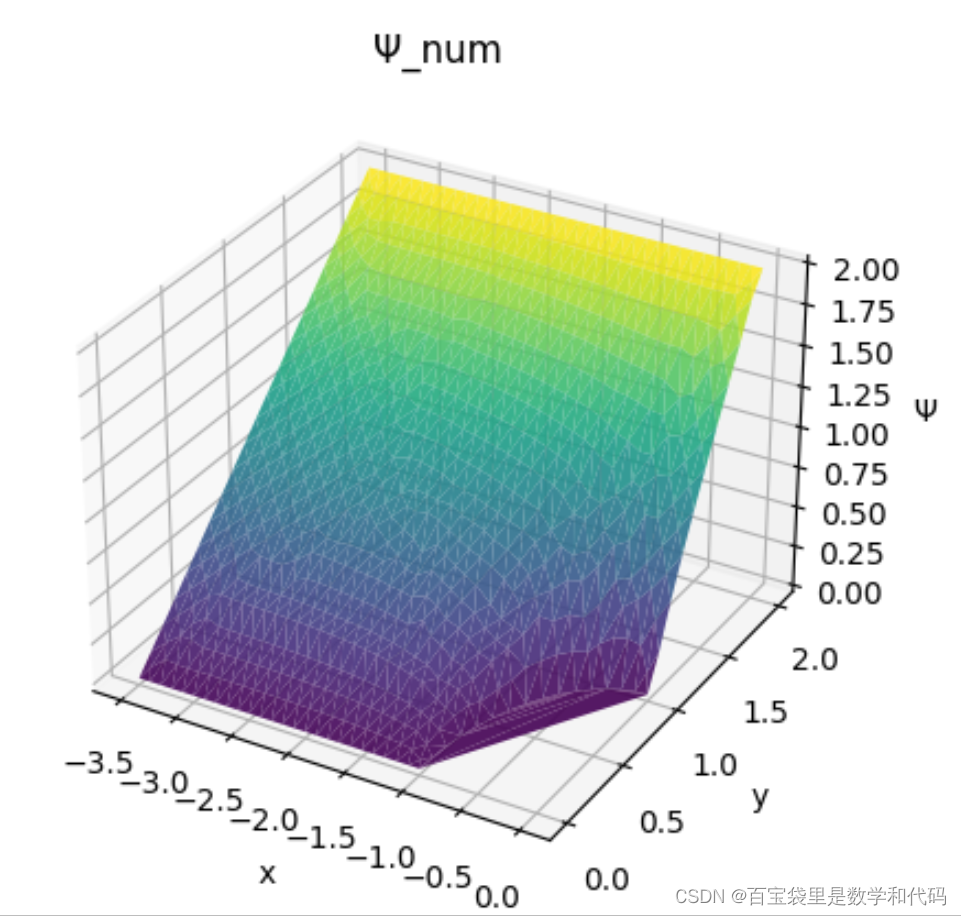

二、数值解的流线图

#二、绘制数值解的流线图
z = Ψ
# 绘制等值线
levels = np.linspace(z.min(), z.max(), 30)
plt.pyplot.tricontour(tri, z, levels=levels, colors='k')
# 添加等值线标签
plt.pyplot.tricontourf(tri, z, levels=levels, cmap='viridis')
plt.pyplot.colorbar()
plt.pyplot.title('streamline _num')
plt.pyplot.show()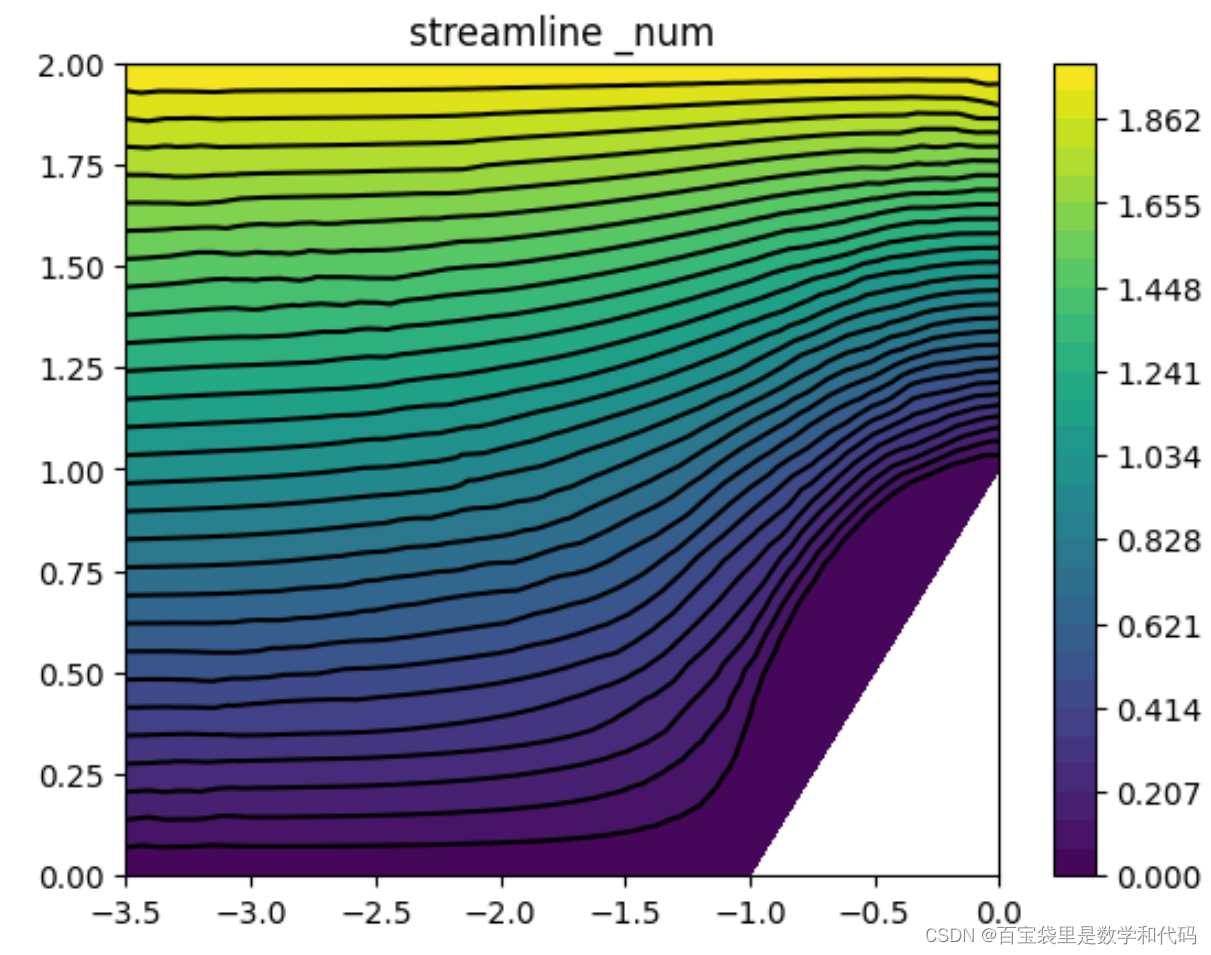

对比：解析解的流线图

# 三、绘制解析解的流线图
#解析解
Ψ_true= np.zeros(NP)
for i in range(NP):Ψ_true[i] = X[i, 1]*(1-1/(X[i,0]**2 + X[i,1]**2))
z = Ψ_true
# 绘制等值线
levels = np.linspace(z.min(), z.max(), 30)
plt.pyplot.tricontour(tri, z, levels=levels, colors='k')
# 添加等值线标签
plt.pyplot.tricontourf(tri, z, levels=levels, cmap='viridis')
plt.pyplot.colorbar()
plt.pyplot.title('streamline _true')
plt.pyplot.show()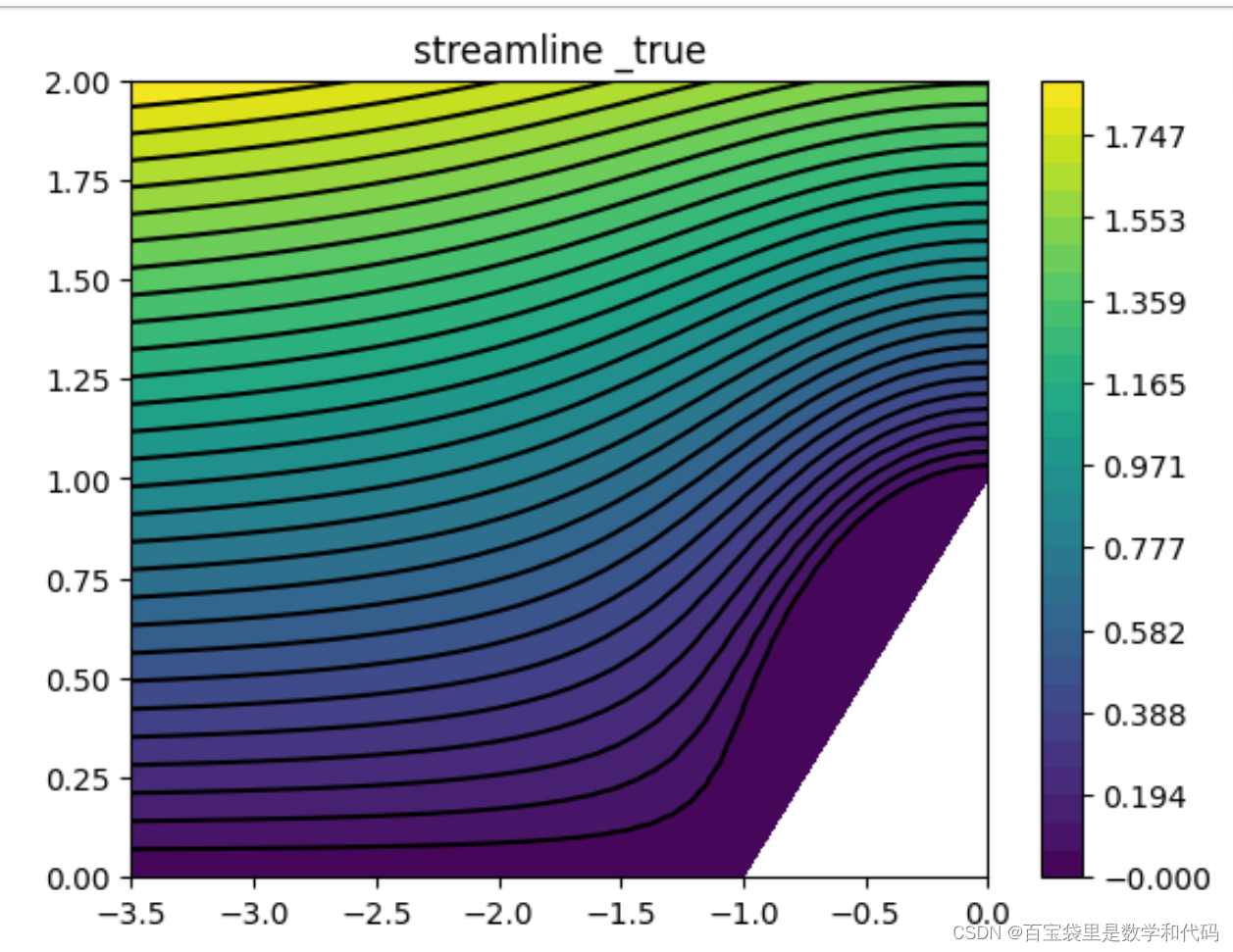

可以观察到数值解与解析解的流线形状是比较相近的。

三、节点流速和压强的数值结果

#四、绘制节点压强的3D图
fig = plt.pyplot.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_trisurf(X[:, 0], X[:, 1], p_node, triangles=tri.triangles, cmap='viridis',alpha = 0.9)
ax.set_title('pressure')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('p')
plt.pyplot.show()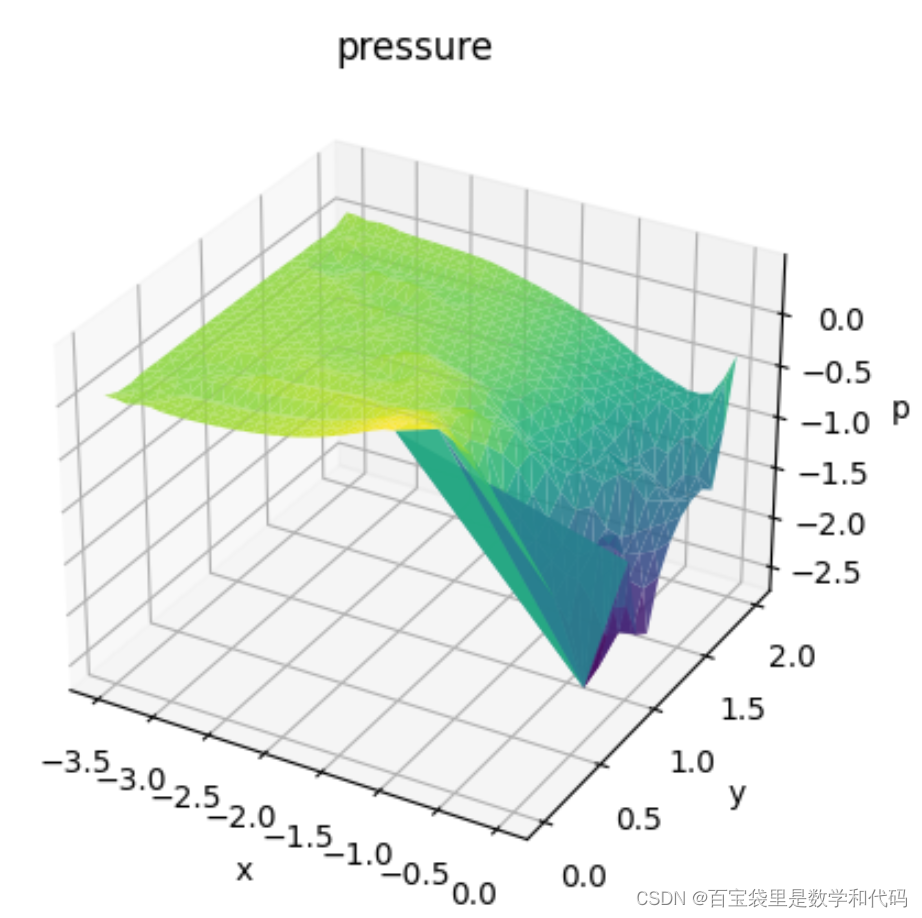

#五、绘制节点流速的3D图
fig = plt.pyplot.figure()ax = fig.add_subplot(121, projection='3d')
ax.plot_trisurf(X[:, 0], X[:, 1], vx_node, triangles=tri.triangles, cmap='viridis',alpha = 0.9)
ax.set_title('vx')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('vx')ax = fig.add_subplot(122, projection='3d')
ax.plot_trisurf(X[:, 0], X[:, 1], vy_node, triangles=tri.triangles, cmap='viridis',alpha = 0.9)
ax.set_title('vy')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_zlabel('vy')plt.pyplot.show()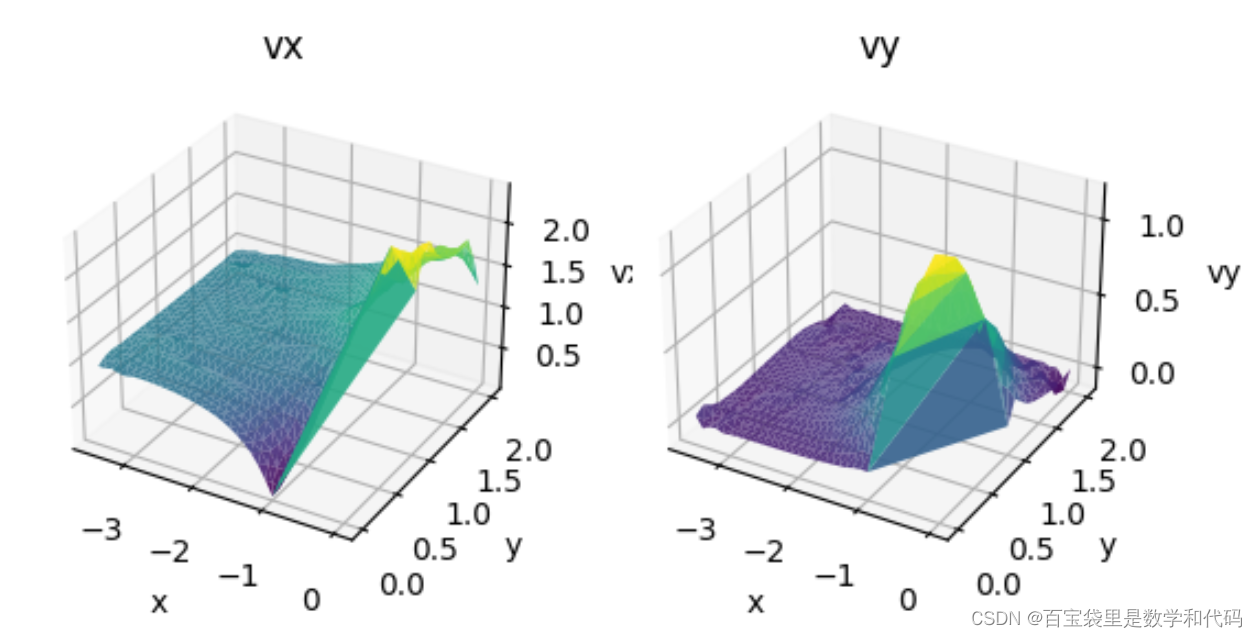

数值解在圆柱壁面附近出现较大的波动。