DFT音频还原及降噪实战

本文主要是介绍DFT音频还原及降噪实战，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

傅里叶变换与信息隐写术(二)

声音数据

​ 声音可以用连续的波形来表示
​ 声音在计算机中的存储是离散的
​ 计算机中存储的是声音的几个采样点的数据，1 秒钟采样 5 个点就表示采样频率是 5 Hz（每隔 0.25 秒取一个点，注意第 0 秒也取）
​ 采样频率越高，听到的声音就越平滑、越连续

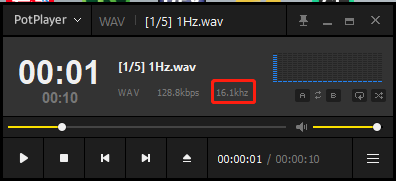
​ 比如这段1Hz的音频采样频率为16.1kHz，就意味着它在这份文件中1 秒钟存储了 16100 个数据点。
​

​ 以下代码可以用于生成一段音频

#!/usr/bin/env python
# coding=utf-8import wave
import numpy as npframeRate = 16100 # 将采样率设置为1.61kHz
time = 10         # 要输出的声音文件的时间长度
volumn = 40       # 声音文件最大大小
pi = np.pi        # 用于表示正弦波
t = np.arange(0, time, 1.0 / frameRate) # 需要在哪些点上进行取样def gen_wave_data(fileName, realF):wave_data = volumn * np.sin(2.0 * pi * realF * t); # 2pi*真实频率*总时长wave_data = wave_data.astype(np.int8)f = wave.open(fileName, "wb")f.setnchannels(1)                   # 声道数，可以理解为立体度f.setsampwidth(1)                   # 采样位宽，表示多少个字节表示一个数据点（1字节：0-256  2字节：0-65535），可以理解为分辨率f.setframerate(frameRate)           # 多少数据代表1秒的音频f.writeframes(wave_data.tostring()) # 把声音数据写到文件中f.close()print("write data to : " + fileName)gen_wave_data("1Hz.wav", 1)
gen_wave_data("2Hz.wav", 2)
gen_wave_data("3Hz.wav", 3)
gen_wave_data("4Hz.wav", 4)
gen_wave_data("5Hz.wav", 5)

运行结果如下图所示

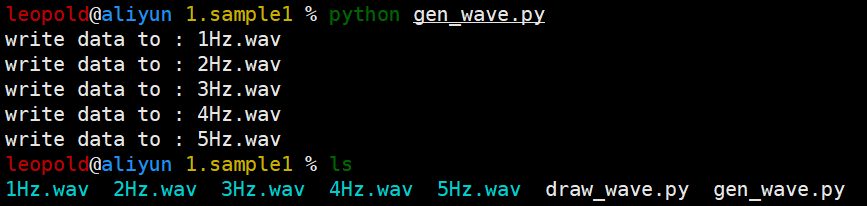
接着，我们可以尝试用代码对我们生成的音频进行绘图，完整代码如下

#!/usr/bin/env python
# coding=utf-8import wave
import matplotlib
matplotlib.use("TkAgg")
import matplotlib.pyplot as pl
import numpy as npdef draw_wave_data(fileName, plotNum):f = wave.open(fileName, "rb")params = f.getparams()             # 参数params在下面有解释str_data = f.readframes(params[3]) # 将所有数据以字符串形式读出f.close()wave_data = np.fromstring(str_data, dtype = np.int8) # 将字符串数据转换成数值数据t = np.arange(0, len(wave_data) * 1.0 / params[2], 1.0 / params[2]) # ；总时间 = 总数据量 / 一个分段的数据量；步长 = 1 / 频率pl.subplot(plotNum)pl.title(fileName)pl.plot(t, wave_data)pl.xlabel("time (seconds)")draw_wave_data("1Hz.wav", 321)
draw_wave_data("2Hz.wav", 322)
draw_wave_data("3Hz.wav", 323)
draw_wave_data("4Hz.wav", 324)
draw_wave_data("5Hz.wav", 325)
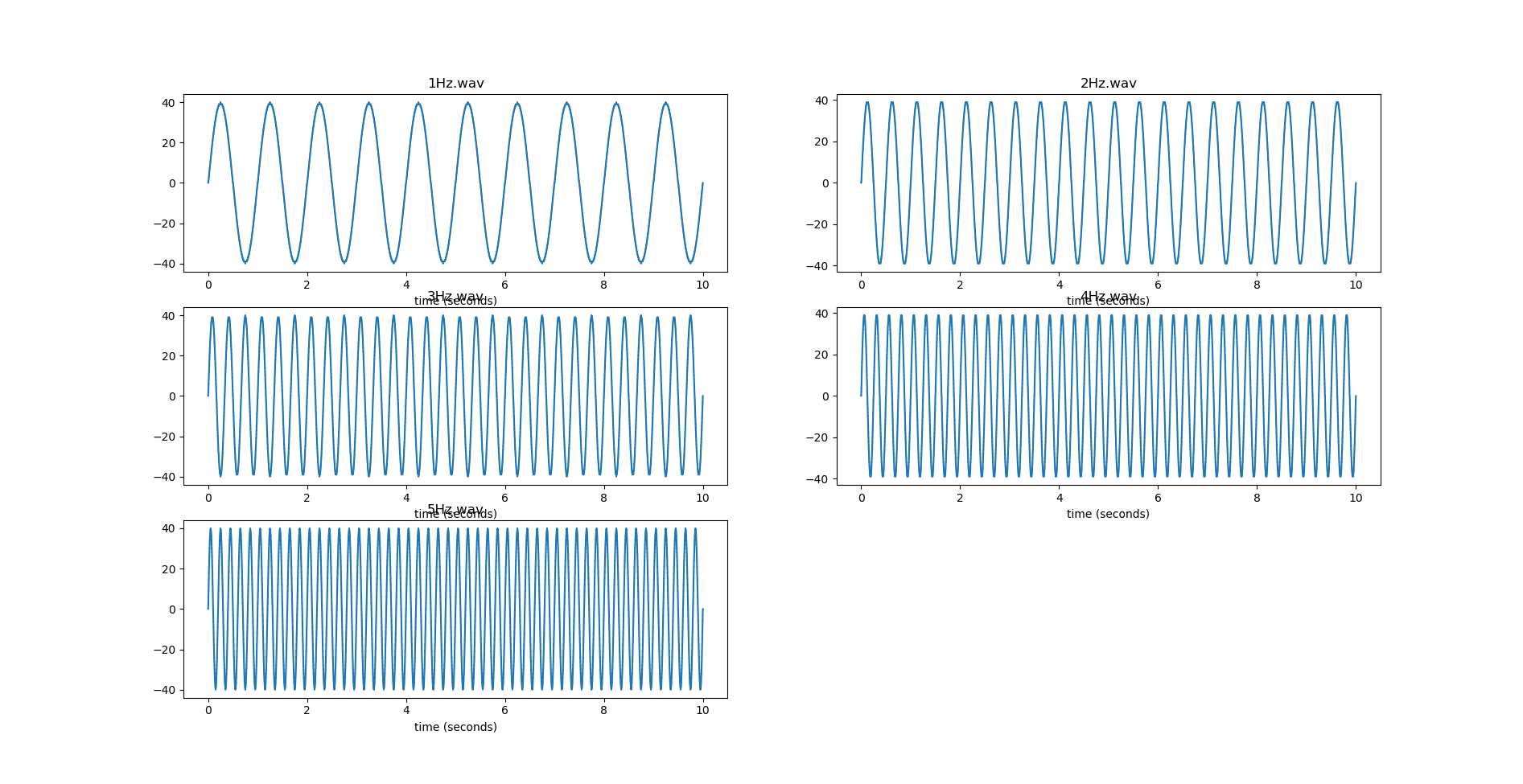
pl.show()

打印参数 params 的内容，结果如下图所示。很明显，前四个参数就是我们之前设置的参数：单声道、1 位宽、采样频率、总时长(总数据量)。

最后运行结果如下

离散傅里叶变换 DFT

​ 离散傅里叶变换主要用于信号分解，给一个合成得到的波形，DFT 可以将其中包含的多种不同频率的波形区分出来。公式（1）如下图所示，其中 x(n) 表示第 n 个声音信号，e 项表示 m 种频率，X(m) 表示第 m 种频率的分析结果。
$$X(m)=\sum _{n=0}^{N-1}x(n)\ast e^{-j2\pi mn/N}\text{\hspace{1em}(1)}$$
​ 上述公式可以理解为，通过上式计算，如果声音数据 x 中包含了第 m 种频率的信号，则 X(m) 会给出第 m 种频率的分析结果（振幅、俯角）。
​ 其中，x 为时域， X 为频域，声音信号是按时间顺序给出，根据 DFT 计算后，声音信号按频率划分。因此，DFT 本质上是实现了时域到频域的转换。
​ 至于 e 项的含义，有以下补充性质
$$\begin{gathered} e^{j2\pi mn/N}={\omega }_n^k=\cos (\frac{2\pi k}{n})+\sin (\frac{2\pi k}{n})i \\ {e}^{-j2\pi mn/N}={\omega }_n^{-k}=\cos (\frac{2\pi k}{n})-\sin (\frac{2\pi k}{n})i \end{gathered}$$
​ 从而，我们上面的公式（1）可以变换为
$$\begin{gathered} X(m)=\sum _{n=0}^{N-1}x(n)\ast {\omega }_N^{-nm} \\ X(m)=\sum _{n=0}^{N-1}x(n)\ast {({\omega }_N^{-m})}^n\text{\hspace{1em}(2)} \end{gathered}$$
​ 进一步，上式可以表示为矩阵乘法的形式

实战1 ：声音还原

​ 首先读取要分析的文件

#!/usr/bin/env python
# coding=utf-8import wave
import numpy as npf = wave.open("secret.wav", "rb")
params = f.getparams()            # 读取参数str_data = f.readframes(params[3])
f.close()wave_data = np.fromstring(str_data, dtype = np.int8)output_fileName = "input.data"
fout = open(output_fileName, "w")fout.write(str(params[3]) + "\n")
for x in wave_data:fout.write(str(x) + "\n")
fout.close()
print("write wave to : " + output_fileName)

​ 最后的效果是得到了 161000 个数值，存入 input.data中去（也可以侧面看出 secret.wav 是一段 10 秒的音频）

​ 接下来实现一下 DFT 算法，大部分都可以照搬 FFT 的代码，只不过对照（2）式的矩阵乘法表示可以看出这里使用的是逆运算，因此稍作修改

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
#include <stack>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <vector>
#include <math.h>
using namespace std;class Complex {
public :Complex(double r = 0.0, double i = 0.0) : r(r), i(i) {}Complex &operator*=(const Complex &rhl) {double a = r, b = i, c = rhl.r, d = rhl.i;r = a * c - b * d;i = a * d + b * c;return *this;}double m() { return sqrt(r * r + i * i); }    # 求复数模值Complex operator*(const Complex &rhl) const {Complex ret(*this);ret *= rhl;return ret;}Complex &operator+=(const Complex &rhl) {r += rhl.r;i += rhl.i;return *this;}Complex operator+(const Complex &rhl) const {Complex ret(*this);ret += rhl;return ret;}Complex &operator-=(const Complex &rhl) {r -= rhl.r;i -= rhl.i;return *this;}Complex operator-(const Complex &rhl) const {Complex ret(*this);ret -= rhl;return ret;}Complex &operator/=(const double x) {r /= x;i /= x;return *this;}Complex operator/(const double x) const {Complex ret(*this);ret /= x;return ret;}double r, i;
};ostream &operator<<(ostream &out, const Complex &a) {out << a.r << "+" << a.i << "i";return out;
}struct FastFourierTransform {#define PI acos(-1)void __transform(vector<Complex> &a, int n, int type = 1) {if (n == 1) { return ; }int m = n / 2;vector<Complex> a1(m), a2(m);for (int i = 0; i < m; i++) a1[i] = a[i << 1], a2[i] = a[i << 1 | 1];__transform(a1, m, type);__transform(a2, m, type);Complex wn(1, 0), w1(cos(2.0 * PI / n), type * sin(2.0 * PI / n));for (int i = 0; i < m; i++) {a[i] = a1[i] + wn * a2[i];a[i + m] = a1[i] - wn * a2[i];wn *= w1;}return ;}vector<Complex> dft(vector<Complex> &a, int n) {vector<Complex> temp(n);for (int i = 0, m = a.size(); i < m; i++) temp[i] = a[i];__transform(temp, n, -1);          # 面对正向变换，type置-1（w_n^{-k}）return temp;}vector<Complex> idft(vector<Complex> &a, int n) {vector<Complex> temp(n);for (int i = 0, m = a.size(); i < m; i++) temp[i] = a[i];__transform(temp, n);              # 面对逆向变换，type置1（w_n^k）for (int i = 0; i < n; i++) temp[i] /= n;return temp;}#undef PI
} fft;int main() {int n, N = 1;cin >> n;             n /= 100;vector<Complex> x(n); # 表示时域信号，一共有n项for (int i = 0; i < n; i++) cin >> x[i].r; # 读入时域信号的值while (N < n) N <<= 1; # N是2的整数次方vector<Complex> X = fft.dft(x, N); # 离散傅里叶变换，变换为频域信号for (int i = 0; i < N; i++) {cout << X[i].r << " " << X[i].i << " ";cout << X[i].m() * 2.0 / N << endl;      # X的模值（实部平方加虚部平方开根号），即复平面上线段长度}return 0;
}

运行结果如下，这就是离散傅里叶的分析结果

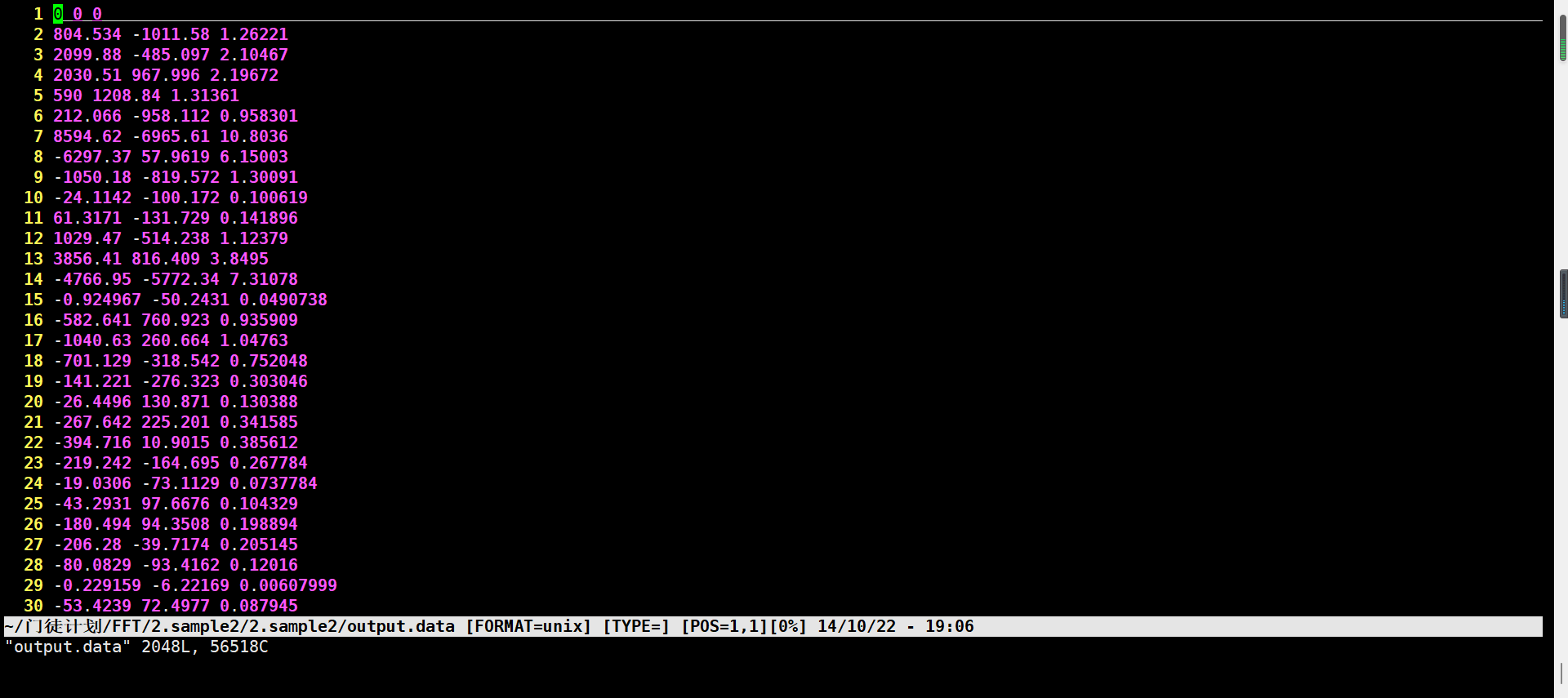
​ 现在分析结果不太直观，我们用程序将它画进图里

#!/usr/bin/env python
# coding=utf-8import wave
import matplotlib
matplotlib.use("Agg")
import matplotlib.pyplot as pl
import numpy as npdef draw_wave_data(x, y, plotNum, title):pl.subplot(plotNum)pl.title(title)pl.plot(x, y)fin = open("output.data", "r")
data = [x.split(" ") for x in fin.read().strip().split("\n")]
data = np.array(data)
data = data.Tx =  np.arange(0, len(data[0]))
draw_wave_data(x, data[0], 221, "Real part")
draw_wave_data(x, data[1], 222, "Imag part")
draw_wave_data(x, data[2], 223, "Mag")pl.show()

运行结果如下图所示

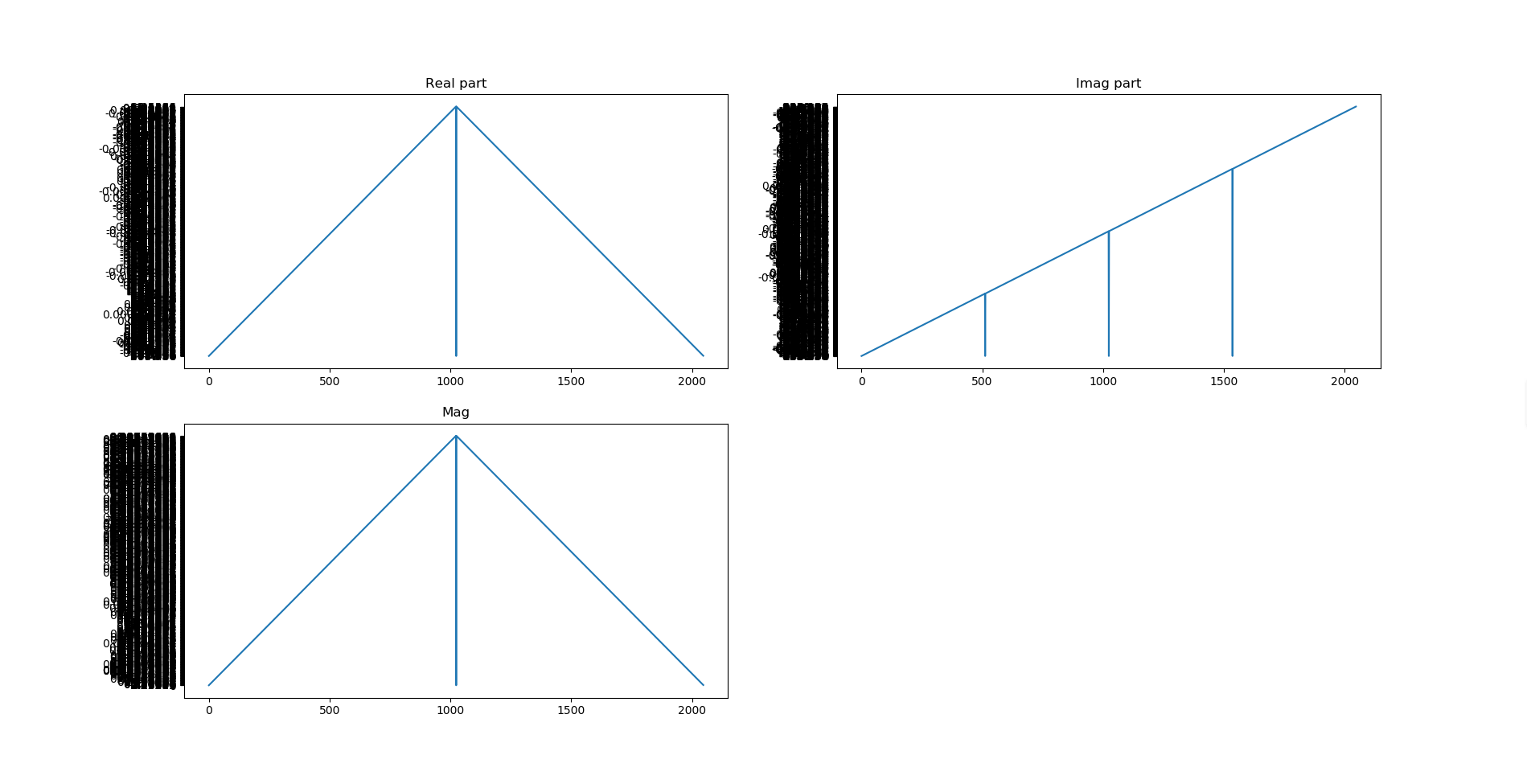
从结果可以看出以下信息

实战2 ：声音降噪

​ 下图是经傅里叶变换后的声音，表示每一种频域的振幅（对称，越接近中间越是高频信号）

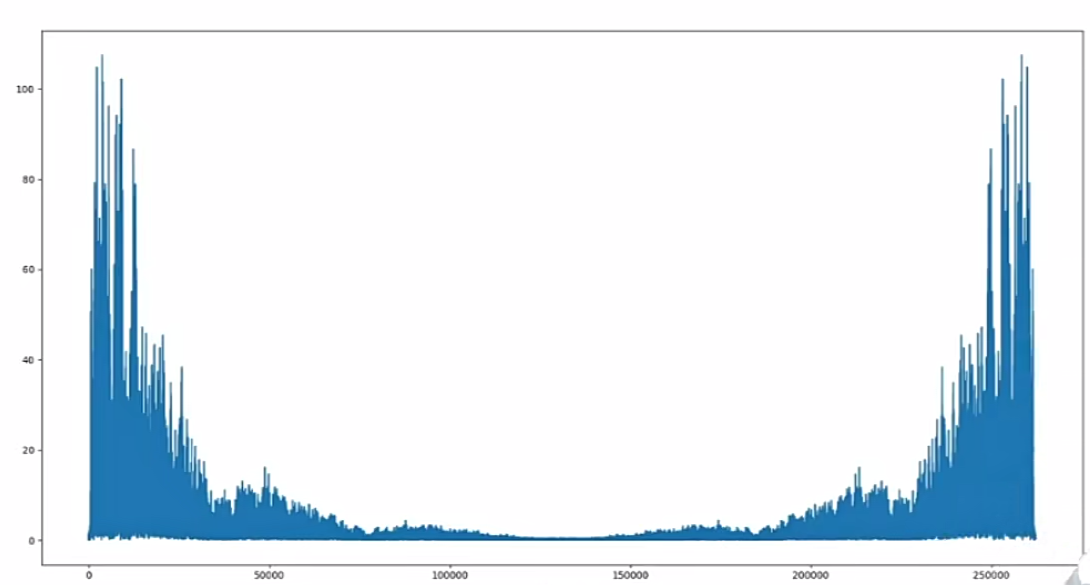
​ 噪音：声音比较小，频率比较高

​ 过滤所有高频信号，然后将频域写回时域

// 将上面dft.cpp的main函数部分进行如下改动
int main() {int n, N = 1;cin >> n;vector<Complex> x1(n);for (int i = 0; i < n; i++) cin >> x1[i].r;while (N < n) N <<= 1;vector<Complex> X = fft.dft(x1, N); // X中存储的是经傅里叶变换后的频域数据for (int k = N / 4, i = N / 2 - k, I = N / 2 + k; i < I; i++) X[i].clear(); // 我们删除中间n/4+n/4=n/2的数据vector<Complex> x2 = fft.idft(X, N); // 将频域数据写回时域for (int i = 0; i < n; i++) cout << int(x2[i].r) << endl;return 0;
}

X = fft.dft(x1, N); // X中存储的是经傅里叶变换后的频域数据
for (int k = N / 4, i = N / 2 - k, I = N / 2 + k; i < I; i++) X[i].clear(); // 我们删除中间n/4+n/4=n/2的数据
vector x2 = fft.idft(X, N); // 将频域数据写回时域
for (int i = 0; i < n; i++) cout << int(x2[i].r) << endl;
return 0;
}

[外链图片转存中...(img-DEgV0c6L-1702784603248)]

这篇关于DFT音频还原及降噪实战的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---