本文主要是介绍6.23删除二叉搜索树中的节点(LC450-M),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
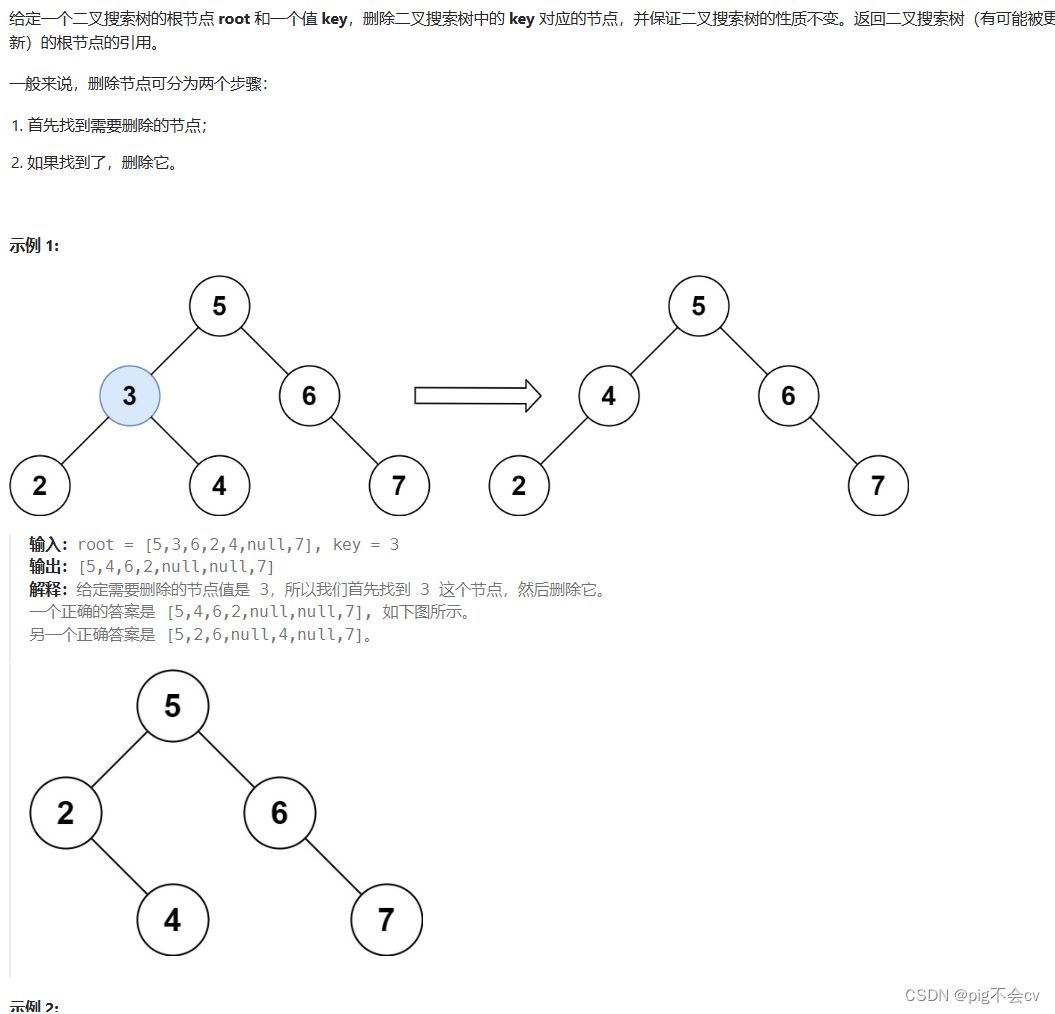
算法:
一共有五种可能的情况:
- 第一种情况:没找到删除的节点,遍历到空节点直接返回了
- 找到删除的节点
- 第二种情况:左右孩子都为空(叶子节点),直接删除节点, 返回NULL为根节点
- 第三种情况:删除节点的左孩子为空,右孩子不为空,删除节点,右孩子补位,返回右孩子为根节点
- 第四种情况:删除节点的右孩子为空,左孩子不为空,删除节点,左孩子补位,返回左孩子为根节点
- 第五种情况:左右孩子节点都不为空,则将删除节点的左子树头结点(左孩子)放到删除节点的右子树的最左面节点的左孩子上,返回删除节点右孩子为新的根节点。
第五种情况,比如要删除节点7,可以让它的左孩子或者右孩子去继位。这里是让左孩子去继位,左孩子比7小,右孩子比7大,那左孩子应该继位在右孩子的最小的节点的左边,即8左边。然后,让3指向9。
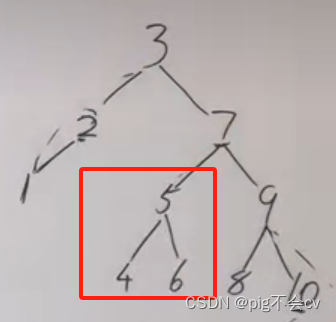
调试过程:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode deleteNode(TreeNode root, int key) { if (root == null) return root;
//1.找不到key节点,自动返回原rootif (root.val == key) {
//2.左右都空,说明是叶子,直接删除if (root.left==null && root.right==null) return null;
//3.左空右不空,右上移if (root.left==null && root.right!=null) {root = root.right;return root;}
//4.右空左不空,左上移 if (root.left!=null && root.right==null) {root = root.left;return root;}
//5.左右都不空,root的左孩子移到右孩子的最左边if (root.left!=null && root.right!=null){TreeNode left = root.left;root = root.right;while (root.left!=null){root = root.left;}root.left = left;return root;}}if (root.val < key) deleteNode(root.left, key); if (root.val > key) deleteNode(root.right, key); return root;}
}
原因:
左右都不空时,代码有问题。
代码逻辑不对,没有中间变量cur,相当于少了个变量cur去实现交换操作。
而且,递归处没有赋值给root.left和root.right(因为这里的递归是有返回值TreeNode的)!!!!无法真正实现递归(这一点老是忘记)
修改后:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode deleteNode(TreeNode root, int key) { if (root == null) return root;
//1.找不到key节点,自动返回原rootif (root.val == key) {
//2.左右都空,说明是叶子,直接删除if (root.left==null && root.right==null) return null;
//3.左空右不空,右上移if (root.left==null && root.right!=null) {root = root.right;return root;}
//4.右空左不空,左上移 if (root.left!=null && root.right==null) {root = root.left;return root;}
//5.左右都不空,root的左孩子移到右孩子的最左边if (root.left!=null && root.right!=null){TreeNode cur = root.right;while (cur.left!=null){cur = cur.left;}cur.left = root.left;root = root.right;return root;}}if (root.val < key) root.left=deleteNode(root.left, key); if (root.val > key) root.right=deleteNode(root.right, key); return root;}
}原因:
递归处逻辑不对。
应该是key比root.val小时,向左搜索
应该是key比root.val大时,向右搜索
正确代码:
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* }*/
class Solution {public TreeNode deleteNode(TreeNode root, int key) { if (root == null) return root;
//1.找不到key节点,自动返回原rootif (root.val == key) {
//2.左右都空,说明是叶子,直接删除if (root.left==null && root.right==null) return null;
//3.左空右不空,右上移if (root.left==null && root.right!=null) {root = root.right;return root;}
//4.右空左不空,左上移 if (root.left!=null && root.right==null) {root = root.left;return root;}
//5.左右都不空,root的左孩子移到右孩子的最左边if (root.left!=null && root.right!=null){TreeNode cur = root.right;while (cur.left!=null){cur = cur.left;}cur.left = root.left;root = root.right;return root;}}if (key< root.val) root.left=deleteNode(root.left, key); if (key> root.val) root.right=deleteNode(root.right, key); return root;}
}时间空间复杂度:
时间复杂度:
O(n),其中 n为 root的节点个数。最差情况下,寻找和删除 cur各需要遍历一次树。
空间复杂度:
O(n),其中 n为 root的节点个数。递归的深度最深为 O(n)。
这篇关于6.23删除二叉搜索树中的节点(LC450-M)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




