统计杂碎记录

本文主要是介绍统计杂碎记录，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

统计杂碎记录

PS: 记录一些自己平时遇到的数理统计概念，持续更新中，后续补充学习

1. nested random intercept effects
建议参考：Visualizing Nested and Cross Random Effects

2. 方差膨胀因子Variance Inflation Factor (VIF)
这个概念呢其实在做PCA, RDA或者其它类似的分析时可能会用到。
首先要知道多重共线性：当解释变量之间存在一定程度的相关性（近似共线性）时，也可以称之为多重共线性。
这会造成什么后果呢？当有多重共线性的情况发生时，参数估计的结果不再具有有效性，因此，在进行逻辑回归之前，我们需要通过VIF检验来排除掉某些有多重共线性的变量。通常，当VIF>10时，就认为存在多重共线性，该特征需要删除。

VIF指的是解释变量之间存在多重共线性时的方差与不存在多重共线性时的方差之比，可以反映多重共线性导致的方差的增加程度。
$=\frac{1}{1-R^{2}}$

这里的R²，即线性回归中的决定系数，可以由因变量和自变量之间的复相关系数的平方得到。
为了得到每一个变量的 VIF，我们需要以每一个变量为因变量对其余所有变量进行线性回归，对每一个变量得到各自的R²，再计算每一个变量的 VIF。

具体计算例子可参考
数理统计基础——多重共线性、方差膨胀因子和决定系数

3. 置换多元变量分析/置换多元方差分析（Permutational multivariate analysis of variance，PERMANOVA）
当因变量不止一个时，即一个或多个因子变量对应了多个因变量时，可使用多元方差分析（MANOVA）。
但是其条件非常苛刻，要求数据满足多元正态性、方差-协方差矩阵同质性，大部分案例中都是直接拒绝的。

这里补充一下协方差矩阵：
【多维随机变量的协方差矩阵】对多维随机变量X=[X₁, X₂, X₃, … , X_n]^T 我们需要计算各维度两两之间的协方差，这样各协方差就组成了一个 n x n 的矩阵，成为协方差矩阵。协方差矩阵是个对称矩阵，对角线上的元素是各维度上随机变量的方差（其实就是方差-协方差矩阵）。定义协方差矩阵为∑，矩阵内的元素 ∑_ij 为：
$\displaystyle\sum_{ij} =cov(X_i, X_j)=E[(X_i-E(X_i))(X_j-E(X_j))]$

替代方法可选择稳健MANOVA，或者而非参数的方法，常用置换多元方差分析（PERMANOVA），又称非参数多因素方差分析（nonparametric multivariate analysis of variance），或Adoins分析，其本质是基于F统计的方差分析，依据距离矩阵对总方差进行分解的非参数多元方差分析方法。可利用半度量（如Bray-Curtis）或度量距离矩阵（如Euclidean）对总方差进行分析，通过线性模型分析不同组因素或环境因子（如临床表型数据、土壤理化指标等）对样品差异的解释度，并用置换检验进行显著性分析。
使用PERMANOVA可分析不同分组因素对样品差异的解释度，并使用置换检验进行显著性统计。

这里再补充一下， MRPP多响应置换过程分析（Multiple Response Permutation Procedure）。用来检验组间（两组或多组）的差异是否显著大于组内差异。与ANOSIM分析类似，可利用半度量或度量距离矩阵计算A值表示组间差异，使用置换检验对分组进行显著性分析。
还有一个，ANOSIM相似性分析。是一种非参数检验，用于检验高纬度数据间的相似性，比较组间和组内差异的大小，从而判断分组是否有意义。可以用于检验两组的组间和组内差异，也可以用于多组。
原理如下，以最基本的两个组为例：
现一共有6个样本，根据我们的实验方案将其氛围两组，Group1和Group2，每组含有3个样本。
1 首先基于组内样本间的距离计算组内的相似性
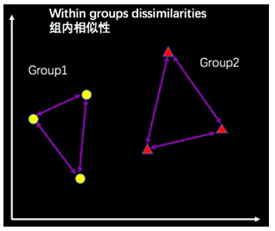
在这里插入图片描述
2 基于组间的距离计算组间的相似性

结合组内和组间，得到：

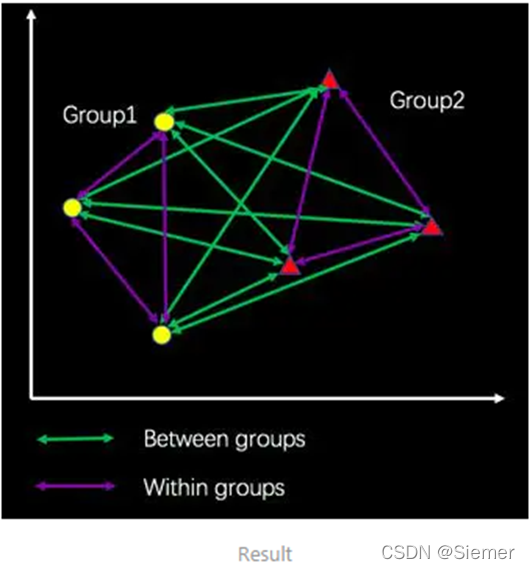
然后根据公式计算R值：

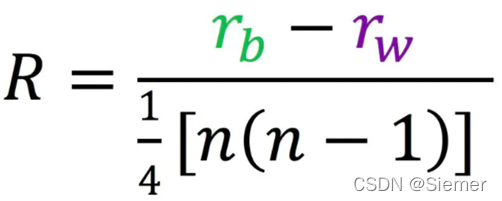
r_b 和 r_w分别为组间和组内差异性秩的平均值；n 即样本数量
因此，R 取值范围为 [-1, 1]：
当R趋向于1时，说明组间差异大于组内差异；
当 R=0 时，说明组间没有差异，即分组无效，不同分组之间没有差异；
当 R 趋向于 -1 时，说明组间差异小于组内差异。
当 R>0 时，还要进一步检验这种差异是否具有可信度，ANOSIM中对其的检验方法也是使用置换检验。