本文主要是介绍利用卡诺图对逻辑表达式进行化简,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、循环码
1. 循环码的定义
又称做格雷码。格雷码属于可靠性编码,是一种错误最小化的编码方式,因为,自然二进制码可以直接由数/模转换器转换成模拟信号,但某些情况,例如从十进制的3转换成4时二进制码的每一位都要变,使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点,它是一种数字排序系统,其中的所有相邻整数在它们的数字表示中只有一个数字不同。它在任意两个相邻的数之间转换时,只有一个数位发生变化。它大大地减少了由一个状态到下一个状态时逻辑的混淆。另外由于最大数与最小数之间也仅一个数不同,故通常又叫格雷反射码或循环码。
特点:任何两个相邻的码组中,仅有一位代码不同。
2. 普通二进制吗与格雷码之间的转换方法
二进制码→格雷码(编码):从最右边一位起,依次将每一位与左边一位异或(XOR),作为对应格雷码该位的值,最左边一位不变(相当于最左边的高位是0);
格雷码→二进制码(解码):从左边第二位起,将每位与左边一位解码后的值异或,作为该位解码后的值(最左边一位依然不变)。
下表为几种自然二进制码与格雷码的对照表:
| 十进制数 | 自然二进制数 | 格雷码 | 十进制数 | 自然二进制数 | 格雷码 |
| 0 | 0000 | 0000 | 8 | 1000 | 1100 |
| 1 | 0001 | 0001 | 9 | 1001 | 1101 |
| 2 | 0010 | 0011 | 10 | 1010 | 1111 |
| 3 | 0011 | 0010 | 11 | 1011 | 1110 |
| 4 | 0100 | 0110 | 12 | 1100 | 1010 |
| 5 | 0101 | 0111 | 13 | 1101 | 1011 |
| 6 | 0110 | 0101 | 14 | 1110 | 1001 |
| 7 | 0111 | 0100 | 15 | 1111 | 1000 |
二、 卡诺图
1. 卡诺图定义
将逻辑变量分成两组,分别在横竖两个方向用循环码形式排列出各组变量的所有取值组合,构成一个有个方格的图形,其中,每一个方格对应变量的一个取值组合,这种图形叫做卡诺图。下图为一个四变量的卡诺图:
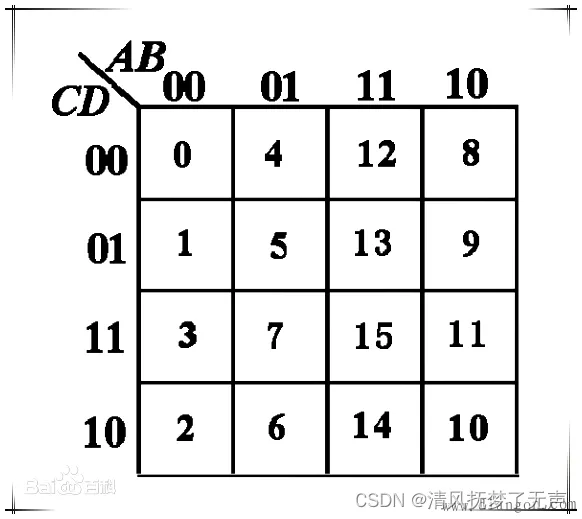
(1)每方格代表一个最小项,方格内的数字表示相应最小项的下标,最小项的逻辑取值填入相应方格;
(2)卡诺图方格外的字母和数字为输入变量及其相应变量取值,变量取值的排序不能改变;
(3)相邻的2个方格称为逻辑相邻项(简称相邻项),相邻项中只有1对变量互为反变量,而其余变量完全相同。
(4)卡诺图一列中最上和最下2个方格是相邻项;一行中最左和最右2个方格是相邻项。
2. 用卡诺图对逻辑表达式进行化简
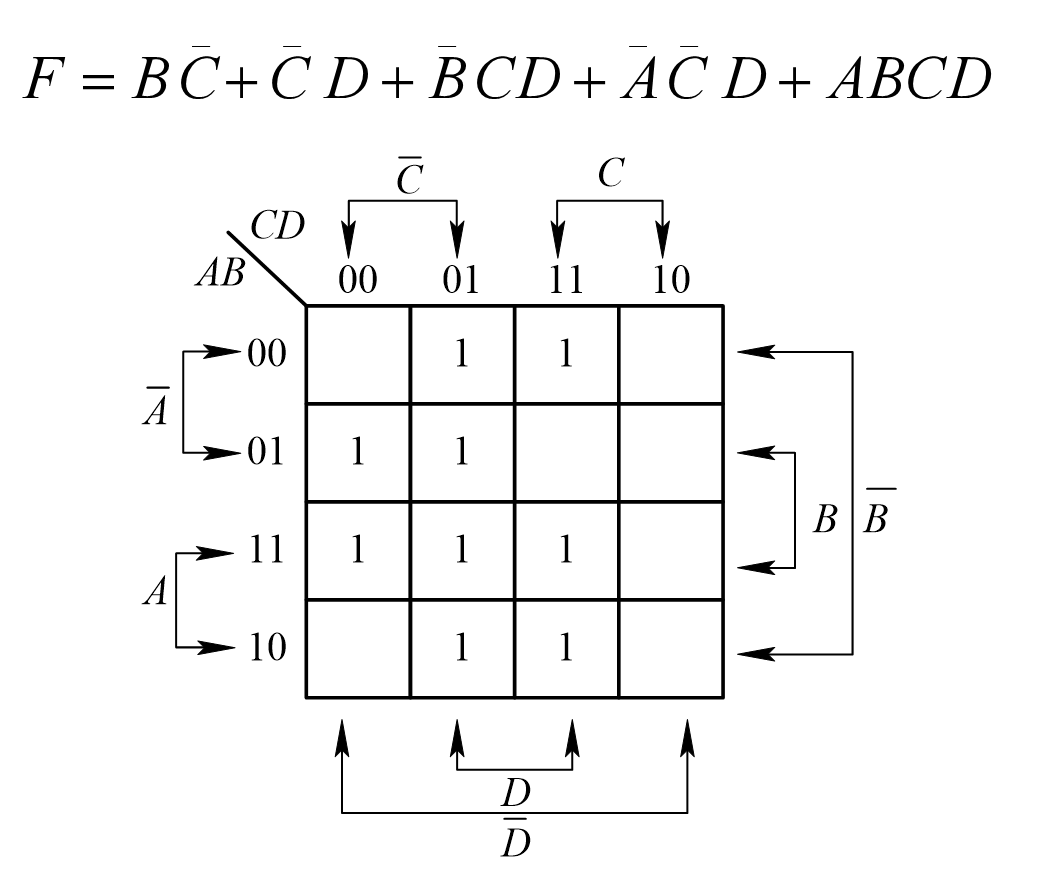
2.1 卡诺图化简的步骤
(1) 将原始函数用卡诺图表示;
(2) 根据最小项合并规律画卡诺圈, 圈住全部“1”方格;
(3) 将上述全部卡诺圈的结果, “或”起来即得化简后的新函数;
(4) 由逻辑门电路, 组成逻辑电路图。
2.2 卡诺图化简的原则
(1)所画的圈必须包含所有的1;
(2)每个圈中包含个1,且至少有一个1是新的;
(3)任一圈中都不能包含取值为0的方格;
(4)圈的个数越少越好,圈越大越好。
要特别注意对边相邻性和四角相邻性。
在进行化简时,如果用图中真值为0的项更方便,可以用他们来处理,方法和真值取1时一样,只是结果要再做一次求反。
补:上述逻辑表达式化简后的结果为。
2.3 含有无关项的化简
约束项(不允许或不会出现的最小项)和任意项(最小项可任意取值)统称为无关项。常用表示。无关项在卡诺图中用×表示,既可看作1,也可看作0,视具体情况而定。
这篇关于利用卡诺图对逻辑表达式进行化简的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








