本文主要是介绍python编程练习:Engquist-Osher差分格式求解Burgers方程,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、题目

二、代码
from scipy.integrate import quad
import numpy as np# 函数f(u)=1/2*u**2,故f`(u)=u
def f_positive(upp_value):# 积分f+(u)中需要使用的函数is_over_zero = int(upp_value > 0)return is_over_zero * upp_valuedef f_negative(upp_value):# 积分f-(u)中需要使用的函数is_over_zero = int(upp_value > 0)return (1 - is_over_zero) * upp_valuedef cal_fu(upp_value, form='+'):""":param upp_value:积分上限:param form: 可选值列表[‘+’,‘-’],决定返回f+(u)还是f-(u):return: quad_r: f+(u)、f-(u)的值"""quad_r = 0if form == "+":quad_r = quad(f_positive, 0, upp_value)[0]elif form == '-':quad_r = quad(f_negative, 0, upp_value)[0]return quad_rdef cal_next_step(pt, px):"""该空间点在下一时间层的值:param pt: 当前点在网格的空间位置:param px: 当前点在网格的时间位置:param grid: 网格点上的值:return:"""u_j_n = grid_value[pt][px] # 计算U(j,n)u_jplus1_n = grid_value[pt][px+1] # 计算U(j+1,n)u_jminus1_n = grid_value[pt][px-1] # 计算U(j-1,n)temp_minus = cal_fu(u_jplus1_n, form='-') - cal_fu(u_j_n, form='-')temp_plus = cal_fu(u_j_n) + cal_fu(u_jminus1_n)u_j_nplus1 = u_j_n - grid_ratio * (temp_minus + temp_plus)grid_value[pt+1][px] = u_j_nplus1if __name__ == "__main__":x_range = [-2, 2] # 空间范围t_range = [0, 0.9] # 时间范围delta_x = 0.1 # 空间步长delta_t = 0.01 # 时间步长grid_ratio = delta_t / delta_x # 网格比grid_x = int((x_range[1] - x_range[0]) / delta_x) + 1 # 空间网格点数,此例中为41grid_t = int((t_range[1] - t_range[0]) / delta_t) + 1 # 时间网格点数,此例中为91# 考虑用列表grid_value来存储Ujn[[t=0.01],...,[t=0.9]]grid_value = np.zeros((grid_t, grid_x)) # 行代表某个时间、列代表某个空间# 将初始值t=0添加到grid_value中,即初始条件for i in range(grid_x):x_current = x_range[0] + delta_x * iif x_current > 0:grid_value[0][i] = 1else:grid_value[0][i] = -1# 将每一个时间层上的左右边界赋固定值grid_value[:, grid_x-1] = 1 # 右边界为1grid_value[:, 0] = -1 # 左边界为-1# 开始计算,时间上索引从0算到89,空间上索引从1算到39# 假设右边界必定收敛for i in range(0, grid_t-1):for j in range(1, grid_x-1):cal_next_step(i, j)grid_value[i, -1] = grid_value[i, -2]grid_value[-1, -1] = grid_value[-1, -2]# 仅将最后一个时间层的网格点数据保存到"2.txt"中np.savetxt('2.txt', grid_value[-1, :], fmt='%0.8f')
三、运行结果
绘图如下:
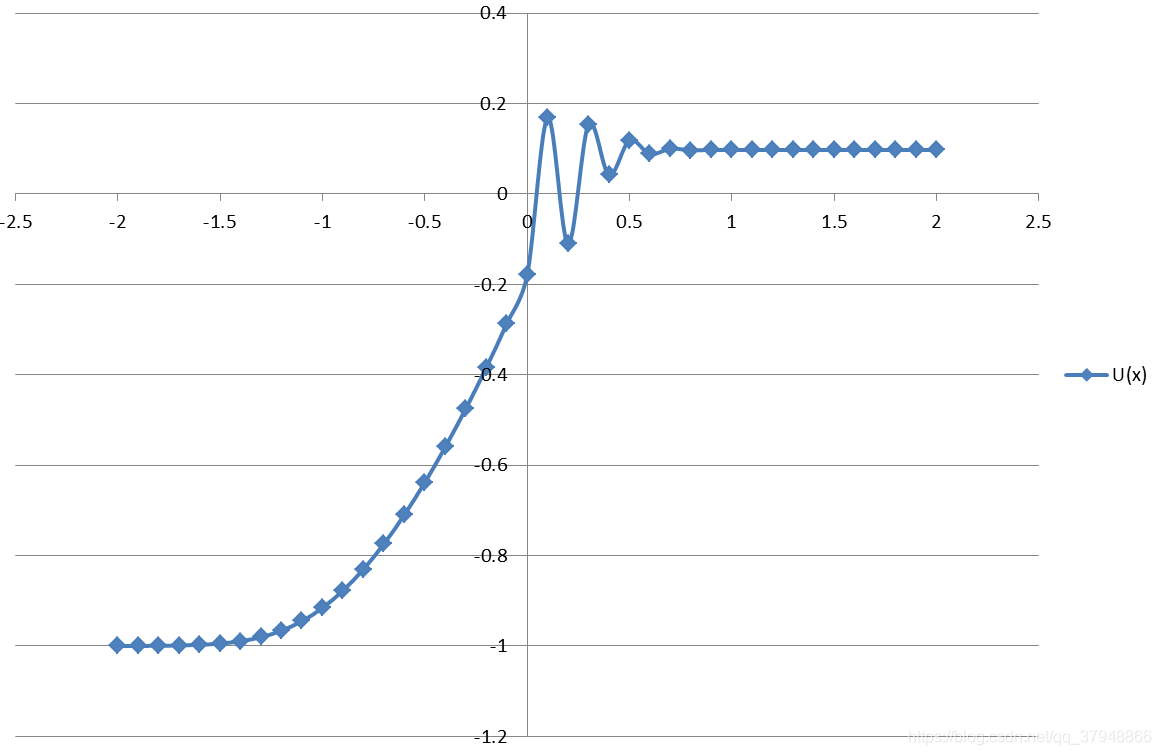
这篇关于python编程练习:Engquist-Osher差分格式求解Burgers方程的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




