本文主要是介绍高项备考葵花宝典-项目进度管理核心方法加强理解-关键路径法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
关键路径法(Critical Path Method,CPM)是一种基于数学计算的项目计划管理方法,是网络图计划方法的一种,属于肯定型的网络图。关键路径法将项目分解成为多个独立的活动并确定每个活动的工期,然后用逻辑关系(结束-开始、结束-结束、开始-开始和开始-结束)将活动连接,从而能够计算项目的工期、各个活动时间特点(最早最晚时间、时差)等。在关键路径法的活动上加载资源后,还能够对项目的资源需求和分配进行分析。关键路径法是现代项目管理中最重要的一种分析工具。
关键路径是指设计中从输入到输出经过的延时最长的逻辑路径。优化关键路径是一种提高设计工作速度的有效方法。在优化设计过程中,关键路径法可以反复使用,直到不可能减少关键路径延时为止。
目录
一、列路径
二、获取关键路径
三、关键路径参数计算
3.1 参数计算
3.2 例题加深巩固1
3.3 例题加深巩固2
一、列路径

图 1
如上图1所示,我们把每个活动的历时标记在活动上,把每个路径上的所有活动历时加在一起,分别所到 4 个路径的总历时,如下图2所示:
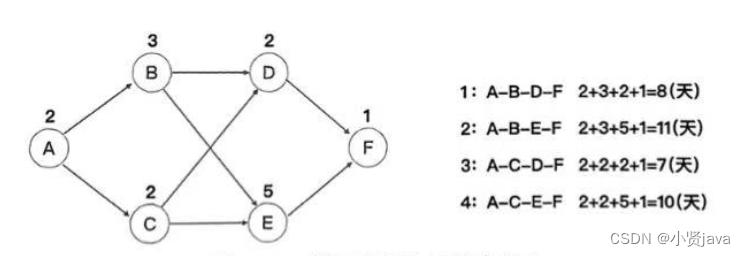
图 2
二、获取关键路径
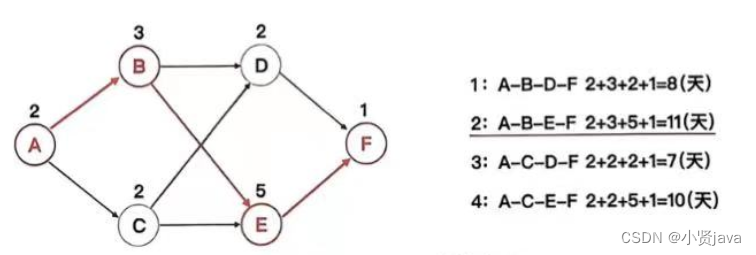
图 3
如图3所示,第二条路径 A-B-E-F 加起来的总历时是11天,是路径中最长的,我条路径就是项目的关键路径,这条路径决定了项目的总工期。
关键路径尖不仅可以帮助我们判断哪条路径决定总工期,而且,学会关键路径参数计算,还能获得很多有价值的信息。
三、关键路径参数计算

图 4
如图4所示,在单代号网格图中,每个活动用一个表格来表示它的参数:
- 最早可以开始的时间(Earliest Start Time, ES):该活动如果有前序活动,那么需要等前序活动完成,它才能开始。ES 就是该活动最早可以时间,取决于前序活动结束的时间。
- 活动历时(Duration,DU):活动历时是用类比尖、专家判断法、三点估算法等方法估算出来的完成活动需要持续的时间。
- 最早可以结果的时间(Earliest Finish Time,EF):我们用最早可以开始的时间(ES)加上活动历时(DU),就可以得到活动最早可以结束的时间(EF = ES + DU)。
- 最晚必须结束的时间(Latest Finish Time,LF):如果该活动有后序活动,而且受总工期制约,必须给后序活动留出足够的时间,那么该活动就必须在某个时间点完成,这个时间点就是最晚必须结束的时间。
- 最晚必须开始的时间(Latest Start Time,LS):我们用最晚必须结束的时间(LF)减去活动历时(DU),就可以得到该活动最晚必须开始的时间(LS = LF - DU)。
- 总浮动时间(Total Float,TF):总浮动时间是 LF 与 EF 之差,或者LS 与ES 之差(TF = LF - EF,TF = LS - ES),这两个差值相等。总浮动时间反映的是在不影响总工期的前提下,该活动可以延后的总时间。
3.1 参数计算

图 5
如上图5所示,我们已经把办公室装修项目分解出 A~ Q共七项活动,而且估算了每项活动的历时,也了解了每项活动的前序活动。
计算:
- 第一步:根据前序活动的依赖关系 ,画出一幅单代号网络图,如下图 6:
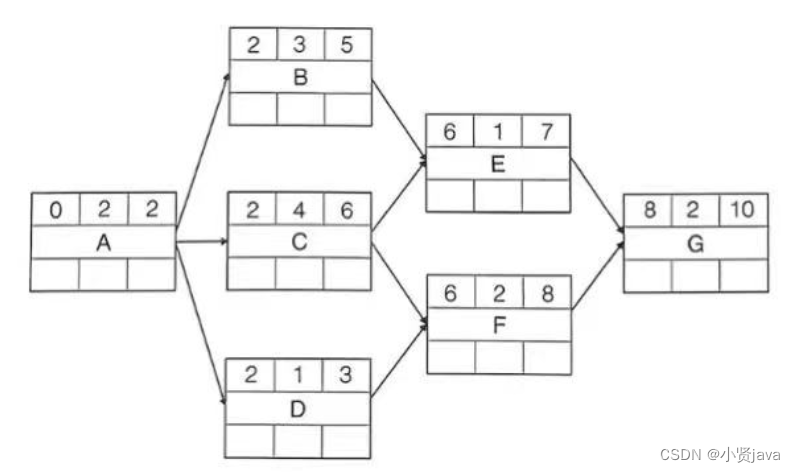
图 6
- 第二步:如上图6所示,填写活动最早可以开始的时间,我们用时间轴上的刻度值来表示,如下图 7所示:
图 7
因为活动A 是第 1 项活动,所以开始时间就是时间轴上的原点 0;活动A历时为 2天,所以最早可以结束时间的时间轴刻度 2 (0 + 2)。
第 2 项活动 B 的前序活动是 A ,活动A 在时间轴刻度 2 的时刻结束,那么活动 B 最早也只能在时间轴刻度 2 这个时刻开始。以此类推,从左向右依次推算出所有活动的最早开始的时间(ES)、活动历时(DU)、最早可以结束的时间(EF)。

图 8
- 第三步:如上图8所示,从最后一项活动 G 开始,从右向左推算活动最晚必须结束时间(LF)、最晚必须开始时间(LS) 和 总浮动时间 (TF)。G 是最后一项活动,如果总工期是 10 天,那么活动 G 的最晚结束时间 (LF)就是时间时刻轴刻度 10,再用减去活动历时 2 天,得到晚晚开始时间 (LS) 就是时间轴刻度 8。
因为活动G 的最晚结束时间 LF 和 最早结束时间EF都是时刻轴刻度10,所以总浮动时间 TF = LF - EF = 10 - 10 = 0。
活动G 的前序活动E,其最晚结束时间(LF)由活动G 的最晚开始时间(LS)决定,所以活动E 的最晚结束时间(LF)是时间轴刻度 8,得到活动E 的最晚开始时间 LS = LF - DU = 8 - 1 = 7。以此类推,从右向左依次推算出每项活动的最晚结束时间(LF)、最晚开始时间(LS)和总浮动时间(TF)。
- 第四步:找到总浮动时间(TF)为0的所有活动,并用红笔标记起来,这条约色的路径就是项目的关键路径;白色的路径 为非关键路径。
绘制成如图8所示,可以看到关键路径上的活动总激动时间均为0,而非关键路径上的活动都有总浮动时间。
3.2 例题加深巩固1
在关键路径上的活动具务什么特征?
- A. 浮动时间 = 0 的活动
- B. 浮动时间 <= 0 的活动
- C. 浮动时间 > 0 的活动
- D. 以上均有可能
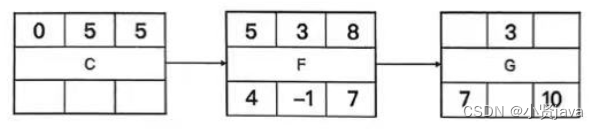
图 9
分析:A,关键路径上的活动的总浮动时间一定为 0 吗?如上图8所示的活动的最早开始时间由前序工作决定,而最晚结束时间由后序工作决定。当我们排计划时,为了满足前序工作C 所需要的 5天工期,F 最早可以开始的时间是时间轴刻度5,加上F需要3天工期,所以F的最早结束时间(EF)是时间轴刻度8;而我们要给F的后序工作G留够3天工期,且总工期不能延误,Gr最晚开始时间(LF)是时间轴刻度 7,所以F 的最晚结束时间就是7。在这种情况下,F的总浮动时间为 -1(7 - 8 = -1)。
总浮动时间为-1:整条路径总时长是10天,C需要5天,G需要7天,那么就只剩下2天,而F也需要3天,那么少的这1天就是总浮动时间 -1。
编制项目进度计划时,如果总工期是固定的,那么就会遇到总浮动时间小于0的情况,即时间不够用。这时利用压缩工期的技术来解决,如加班加人或者后序活动设置提前量,让后序活动提前开始,目的都是在有限的时间内完成这些活动。
分析:B,也不对。比如总工期有时间储备,则关键路径上的活动就有了浮动时间。那么 ABC三项均有可能,正确是D。那么应该描述为总浮动时间最少的路径为关键路径。
3.3 例题加深巩固2
以下关于“关键路径”的表述正确码?
- A. 关键路径决定了项目的总工期
- B. 关键路径所需要的时间最长
- C. 关键路径上的浮动时间最少
- D. 一个项目的关键路径只能有一条
- E. 关键路径上的活动技术含量高
- F. 活动延误可能导致关键路径变化
- G.关键路径上的活动的工期无法压缩
A,正确。关键路径的特征是活动历时加起来最长,最长的路径决定项目总工期。
B,正确。理由同上。
C,正确。3.2 的结论。
D,错误。一个项目关键路径可能不止一条,如果多条路径的总浮动时间都是0,那么这几条路径就都是关键路径。
E,错误。关键路径上的活动只是没有浮动时间或者浮动时间最少,和技术含量无关。即使特别简单、谁都能干的活动,只要它在时间上没有余地,它就在关键路径上。
F,正确。非关键路径 上的活动如果延误,延误时间一亘超过了总浮动时间,那么这条路径就把项目总工期延误了,这条路径也就成了关键路径。由于总工期变长,原来的关键路径反而有了浮动时间,变成了非关键路径。所以,在这种情况下,项目的关键路径发生了变化。
G,错误。关键路径上的活动只是没有时间余地,并不是不能压缩。一般情况下,客户或发起人要求我们压缩工期,就是要我们针对关键路径上的活动进行压缩。
这篇关于高项备考葵花宝典-项目进度管理核心方法加强理解-关键路径法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




