Kalman滤波、扩展Kalman滤波、无迹Kalman滤波和异步滤波的原理及其Matlab代码

本文主要是介绍Kalman滤波、扩展Kalman滤波、无迹Kalman滤波和异步滤波的原理及其Matlab代码，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

引言

本文给出了Kalman Filter（卡尔曼滤波）、Extended Kalman Filter（扩展卡尔曼滤波）、Unscented Kalman Filter（无迹卡尔曼滤波）和Asynchronous Filter（异步滤波）的原理及其Matlab代码。不同的滤波算法以函数形式在不同的m文件，调用即可使用。

Kalman滤波

该部分展示了kalman滤波的代码及其仿真结果。
状态转移模型：
$x(t+1)=Ax(t)+\Gamma w(t)$
其中$x(t)\in R^{n\ast 1}$表示t时刻的状态向量，$A\in R^{m\ast m}$是状态转移矩阵,Γ是噪声系数矩阵，w(t)是t时刻的过程噪声向量, 其为零均值高斯白噪声，协方差阵为Q>0。
量测模型：
$yi(t)=Hix(t)+vi(t)$
,其中$yi(t)$表示t时刻传感器网络中的传感器i的量测向量，$Hi\in R^{l\ast m}$是观测矩阵,vi(t)是t时刻的量测噪声向量，其为零均值高斯白噪声，协方差阵为Ri>0。
初始化:


状态更新:

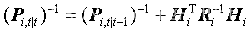
代码及其结果展示

核心代码：（完整代码见文末）

function [estimate, cov_error_estimate] = kalman_filter(measure, x_last,...P_last,flag)
%kalman_filter 基本kalman滤波算法
%   输入：量测值，上一时刻估计，上一时刻估计误差协方差,是否预测的标志
%   输出：当前时刻估计，当前时刻估计误差协方差
% 当flag为1，则跳过预测步骤
%%
% 状态转移矩阵
global A;
% 系统噪声系数矩阵
global gama;
% 系统噪声协方差
global Q;
% 量测矩阵
global H;
% 量测噪声协方差
global R;
%%
% 如果全零，即无初始化
if ~any(x_last)if measure==0estimate = x_last;cov_error_estimate = P_last;else%   如果是0时刻，则取量测值对应的状态为当前时刻估计，9倍的量测误%差协方差阵为当前时刻估计误差协方差。estimate = H\measure;cov_error_estimate = H\(2*(R))/H';end
elseif flag==1forecast=x_last;P_forecast=P_last;elseforecast = A * x_last;P_forecast = (A*P_last *A'+ gama*Q* gama');endif measure==0estimate=forecast;cov_error_estimate = P_forecast;elsekalman_gain = P_forecast*H'/(H*P_forecast*H'+R);estimate = forecast + kalman_gain*(measure - H*forecast);cov_error_estimate = P_forecast - kalman_gain*H*P_forecast;end
end
end

结果展示：

扩展Kalman滤波

扩展卡尔曼滤波是标准卡尔曼滤波在非线性情形下的一种扩展形式，EKF算法是将非线性函数进行泰勒展开，省略高阶项，保留展开项的一阶项，以此来实现非线性函数线性化，最后通过卡尔曼滤波算法近似计算系统的状态估计值和方差估计值,对信号进行滤波。
状态转移方程与量测方程

泰勒线性化


预测步骤

估计步骤

代码及其结果展示

核心代码：（完整代码见文末）

function [estimate, cov_error_estimate] = extend_kf(measure, x_last, P_last,...flag,radar)
%kalman_filter 扩展kalman滤波算法
%   输入：量测值，上一时刻估计，上一时刻估计误差协方差,是否预测的标志,
%雷达的状态信息
%   输出：当前时刻估计，当前时刻估计误差协方差
% 当flag为1，则跳过预测步骤
%%
% 状态转移矩阵
global A;
% 系统噪声系数矩阵
global gama;
% 系统噪声协方差
global Q;
% 量测噪声协方差
global R;
%%
% 如果全零，即无初始化
if ~any(x_last)if measure==0estimate = x_last;cov_error_estimate = P_last;else%   如果是0时刻，则取量测值对应的状态为当前时刻估计，9倍的量测误%差协方差阵为当前时刻估计误差协方差。%   此处为9的原因是3倍的标准差为百分之95的可能的误差值，可以认为%包含了最大误差的情况。estimate=[radar(1,1)+measure(1,1)*cos(measure(3,1))*cos(measure(2,1));radar(2,1)+measure(1,1)*sin(measure(3,1));radar(3,1)-measure(1,1)*cos(measure(3,1))*sin(measure(2,1));0;0;0];cov_error_estimate = 99*[1,0,0,1,0,0;0,1,0,0,1,0;0,0,1,0,0,1;1,0,0,1,0,0;0,1,0,0,1,0;0,0,1,0,0,1];end
elseif flag==1forecast=x_last;P_forecast=P_last;elseforecast = A * x_last;P_forecast = (A*P_last *A'+ gama*Q* gama');endx=forecast(1,1)-radar(1,1);y=forecast(2,1)-radar(2,1);z=forecast(3,1)-radar(3,1);dist = norm([x;y;z]);dist_horiz = norm([x;z]);H=[x/dist,y/dist,z/dist,0,0,0;z/dist_horiz^2,0,-x/dist_horiz^2,0,0,0;-x*y/(dist^2*dist_horiz),dist_horiz/dist^2,-y*z/(dist_horiz*dist^2),0,0,0];z_est = measure_func([x;y;z]);if measure==0estimate=forecast;cov_error_estimate = P_forecast;elsekalman_gain = P_forecast*H'/(H*P_forecast*H'+R);estimate = forecast + kalman_gain*(measure - z_est);cov_error_estimate = P_forecast - kalman_gain*H*P_forecast;end
end
end

结果展示：

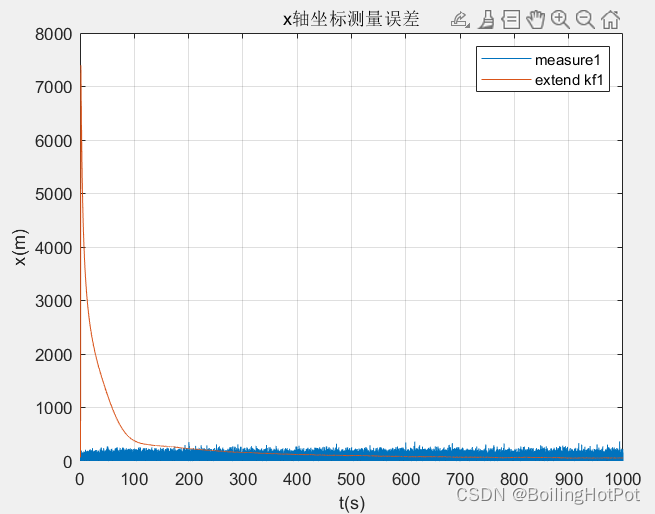
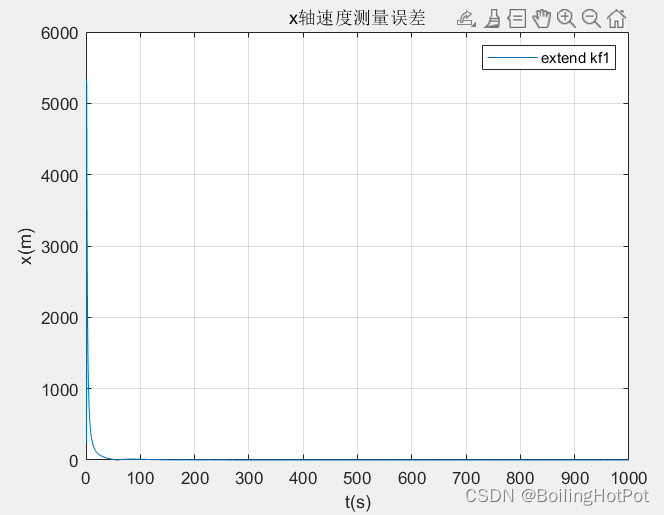
无迹Kalman滤波

无迹变换

设存在一个m维随机向量和n维随机向量z，其中z与x为非线性关系

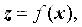
x的均值为，方差为P；x通过非线性映射得到z。无迹变换就是根据x的统计特性，得到一族点集，该点集称为为σ点；将σ点进行非线性映射可以得的新的点集；通过新的点集得到z的统计特性。一般情况下σ点的数目为2n+1。
无迹变换的具体过程可描述如下：
(1)计算2n+1个点及其权系数


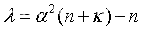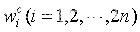其中，决定点的散布程度，通常取正数，通常取为0，β用来代表x的分布情况(正态分布的情况下，最佳值为2)，表示矩阵的平方根的第i列，为用于计算均值的权重，为用于计算方差时的权重。
(2)计算σ点通过非线性函数的传播结果

从而可得



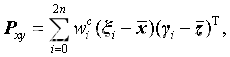
此时，我们得到了无迹变换的结果。

无迹Kalman滤波

针对量测为非线性、状态转移为线性的系统模型，无迹Kalman滤波是用无迹变换进行经典卡尔曼滤波中量测方程的映射。
每个递推无迹Kalman滤波的具体步骤如下：
(1)针对线性目标状态转移模型，对于给定的估计和估计误差协方差，基于经典Kalman滤波求状态预测以及预报误差的协方差阵。

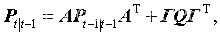
(2)针对非线性传感器量测模型，用无迹变换求σ点，并通过量测方程的传播。
计算σ点，即

计算输出的一步提前预测，即

在获得新的量测后，进行滤波更新，

代码及其结果展示

核心代码：（完整代码见文末）

function [estimate, cov_error_estimate] = unscented_kf(measure, x_last, P_last,...flag,radar)
%kalman_filter 扩展kalman滤波算法
%   输入：量测值，上一时刻估计，上一时刻估计误差协方差,是否预测的标志,
%雷达的状态信息
%   输出：当前时刻估计，当前时刻估计误差协方差
% 当flag为1，则跳过预测步骤
%%
% 状态转移矩阵
global A;
% 系统噪声系数矩阵
global gama;
% 系统噪声协方差
global Q;
% 量测噪声协方差
global R;
%%
% 如果全零，即无初始化
if ~any(x_last)if measure==0estimate = x_last;cov_error_estimate = P_last;else%   如果是0时刻，则取量测值对应的状态为当前时刻估计，9倍的量测误%差协方差阵为当前时刻估计误差协方差。%   此处为9的原因是3倍的标准差为百分之95的可能的误差值，可以认为%包含了最大误差的情况。% TODO 应该设置为根据实际对象进行变化，这里强制设置为6个状态，%后续对无迹滤波和此处进行改变，让其可以根据实际情况进行随动estimate=[radar(1,1)+measure(1,1)*cos(measure(3,1))*cos(measure(2,1));radar(2,1)+measure(1,1)*sin(measure(3,1));radar(3,1)-measure(1,1)*cos(measure(3,1))*sin(measure(2,1));0;0;0];cov_error_estimate = 1*[1,0,0,1,0,0;0,1,0,0,1,0;0,0,1,0,0,1;1,0,0,1,0,0;0,1,0,0,1,0;0,0,1,0,0,1];end
elseif flag==1forecast=x_last;P_forecast=P_last;elseforecast = A * x_last;P_forecast = (A*P_last *A'+ gama*Q* gama');endif measure==0estimate=forecast;cov_error_estimate = P_forecast;else[forecast_point,forecast_weight]=get_point(forecast,P_forecast,size(forecast,1));measure_point = zeros(size(measure,1),size(forecast_point,2));for cou_point = 1:size(forecast_point,2)measure_point(:,cou_point)=measure_func(forecast_point(1:3,cou_point)-radar(1:3,1));endmeasure_expect = sum(forecast_weight(1,:).*measure_point,2);P_z = forecast_weight(2,:).*(measure_point-measure_expect)*...(measure_point-measure_expect)'+R;P_xz = forecast_weight(2,:).*(forecast_point-forecast)*...(measure_point-measure_expect)';kalman_gain = P_xz/P_z;estimate = forecast + kalman_gain*(measure - measure_expect);cov_error_estimate = P_forecast - kalman_gain*P_z*kalman_gain';end
end
end

结果展示：

异步无迹Kalman滤波

在目标状态估计过程中，量测通常以离散化采样给出，同时带有一个探测时间标志。分布式传感器网络是对多个量测进行处理。由于传感器网络传输存在随机的时间延迟，且各个节点对于量测的预处理时间存在随机性，很可能出现源于某个目标的较晚的量测到达某一节点后较早的量测才到达该节点，这种情况就称为非顺序量测。在目标状态估计过程中，传感器节点通常仅保存航迹的充分统计量。这样，当接收到一个延迟的量测时，假定该量测的时戳为t，为了实时性，估计结果被更新到tz>t时刻，此时需要使用来自时刻t的量测更新tz时刻的估计。这就是在实际的多传感器系统中常见的负时间量测更新问题，原因是t-tz为负，而在标准的滤波问题中总假定为非负。通常情况下的滤波算法不适用于这种情况，因此，就需要对适用于异步滤波的算法进行研究。

原理

首先，我们需要对非线性目标运动模型以不同的时间间隔进行重新的离散化定义。对于任意时间间隔的状态转移矩阵为；任意时间间隔的噪声系数矩阵为；任意时间间隔的系统噪声为

本文仅研究高斯白噪声随机过程，则根据随机积分的性质可知，离散化后的系统噪声仍为均值为0的高斯白噪声，其协方差矩阵为

为了便于描述，假定当前时刻为t，而最新的量测时刻为td，且td的量测为t时刻的延迟量测，也就是说

此时，

其中，d为td时刻的简化标记。可以得到

其中为的逆矩阵，表示后向状态转矩矩阵。
我们要解决的问题为：在t时刻，已知目标的状态估计和估计误差协方差。同时，我们得到了td时刻的量测。此时，需要用td时刻的量测来更新t时刻状态估计和估计误差协方差，即计算

其中。
在最小均方误差准则下，对于非顺序量测问题的最优更新算法为

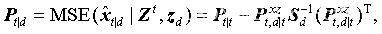
其中，

为了求出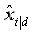，我们需要得到Kd和的值。首先

其中

由传感器探测模型及最小均方误差准则得

可知，

其中

的σ点为

根据传感器探测模型，得

求得计算的σ点为

同理，根据已知的，求得计算的σ点为

计算量测的一步提前预测，即

可知

此时，因为等于0，可得。由最小均方误差准则可得

带入式子可求。根据式子可得与

可得的σ点为

根据非线性变换，可得的σ点为

由的σ点可求

可得Kd；将Kd和的带入可得。接下来，将和带入即可求出。至此，完成了用td时刻的量测来更新t时刻状态估计和估计误差协方差。

代码及其结果展示

核心代码：（完整代码见文末）

function [estimate, cov_error_estimate] = unscented_aysn(measure_aysn,t_asyn,...x_last, P_last,flag,radar,last_est_last,last_P_last,measure)
%kalman_filter 扩展kalman滤波算法
%   输入：量测值，上一时刻估计，上一时刻估计误差协方差,是否预测的标志,
%雷达的状态信息
%   输出：当前时刻估计，当前时刻估计误差协方差
% 当flag为1，则跳过预测步骤
%%
global t_step;
% 状态转移矩阵
global A;
% 系统噪声系数矩阵
global gama;
% 系统噪声协方差
global Q;
% 量测噪声协方差
global R;
%%
last_est_last = A * last_est_last;
last_P_last = (A*last_P_last *A'+ gama*Q* gama');
% 如果全零，即无初始化
if ~any(x_last)if measure_aysn==0estimate = x_last;cov_error_estimate = P_last;else%   如果是0时刻，则取量测值对应的状态为当前时刻估计，9倍的量测误%差协方差阵为当前时刻估计误差协方差。%   此处为9的原因是3倍的标准差为百分之95的可能的误差值，可以认为%包含了最大误差的情况。estimate=[radar(1,1)+measure_aysn(1,1)*cos(measure_aysn(3,1))*cos(measure_aysn(2,1));radar(2,1)+measure_aysn(1,1)*sin(measure_aysn(3,1));radar(3,1)-measure_aysn(1,1)*cos(measure_aysn(3,1))*sin(measure_aysn(2,1));0;0;0];cov_error_estimate = 1*[1,0,0,1,0,0;0,1,0,0,1,0;0,0,1,0,0,1;1,0,0,1,0,0;0,1,0,0,1,0;0,0,1,0,0,1];end
elseif flag==1forecast=x_last;P_forecast=P_last;elseforecast = A * x_last;P_forecast = (A*P_last *A'+ gama*Q* gama');endif measure_aysn==0estimate=forecast;cov_error_estimate = P_forecast;elsenum_state = size(forecast,1);Q_td_t =  Q_t1_t2(t_asyn,t_step);[w_td2t_t_1_point,~] = ...get_point(zeros(num_state,1), Q_td_t,3);[last_est_point,last_est_weight] = ...get_point(last_est_last, last_P_last, 3);measure_t_1_point = zeros(size(measure,1),size(last_est_point,2));for cou_point = 1:size(last_est_point,2)measure_t_1_point(:,cou_point)=measure_func(...last_est_point(1:3,cou_point)-radar(1:3,1));endmeasure_expect_t_1 = sum(last_est_weight(1,:).*measure_t_1_point,2);cov_zt_t_1 = last_est_weight(2,:).*(measure_t_1_point-...measure_expect_t_1)*(measure_t_1_point-measure_expect_t_1)'+R;% TODO 应该修正R后的pointcov_w_td2t_zt_t_1= last_est_weight(2,:).*(w_td2t_t_1_point)*...(measure_t_1_point-measure_expect_t_1)';w_td2t = cov_w_td2t_zt_t_1/cov_zt_t_1*(measure-...measure_expect_t_1);cov_w_td2t_t = Q_td_t-cov_w_td2t_zt_t_1/cov_zt_t_1*...cov_w_td2t_zt_t_1';[forecast_point,forecast_weight]=get_point(forecast,P_forecast,3);% (3-25)backcast = A_t1_t2(t_step,t_asyn)*(forecast-w_td2t);P_backcast = A_t1_t2(t_step,t_asyn)*P_forecast*...(A_t1_t2(t_step,t_asyn))'-A_t1_t2(t_step,t_asyn)*...(cov_w_td2t_t)*(A_t1_t2(t_step,t_asyn))';[backcast_point,backcast_weight]=get_point(backcast,P_backcast,3);measure_expect_t_point = zeros(size(measure,1),size(backcast_point,2));for cou_point = 1:size(backcast_point,2)measure_expect_t_point(:,cou_point)=measure_func(...backcast_point(1:3,cou_point)-radar(1:3,1));endmeasure_expect_t = sum(backcast_weight(1,:).*measure_expect_t_point,2);% (3-36)P_z = backcast_weight(2,:).*(measure_expect_t_point-...measure_expect_t)*(measure_expect_t_point-measure_expect_t)'+R;% (3-37)         % TODO 应该修正R后的pointP_xz = forecast_weight(2,:).*(forecast_point-forecast)*...(measure_expect_t_point-measure_expect_t)';kalman_gain = P_xz/P_z;estimate = forecast + kalman_gain*(measure_aysn - measure_expect_t);cov_error_estimate = P_forecast - P_xz/P_z*P_xz';end
end
end

结果展示：


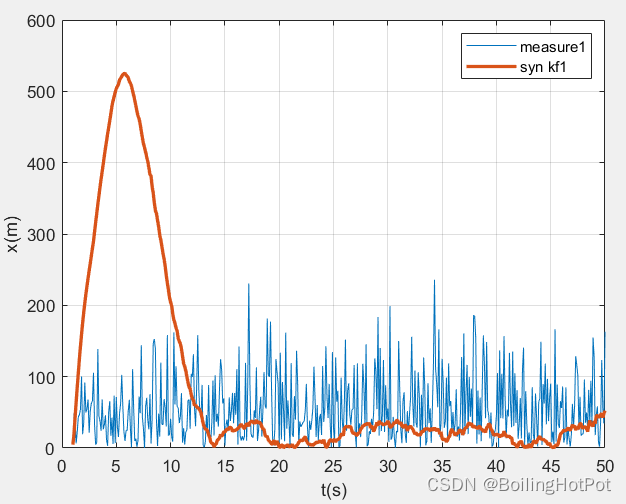
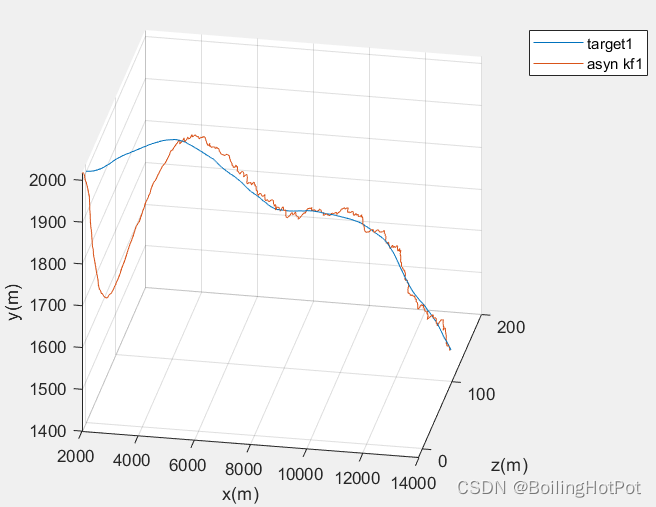
完整代码分为多个文件，数量较多，无法放在文章中。完整代码在公众号（沸腾的火锅资源号）中自取。

这篇关于Kalman滤波、扩展Kalman滤波、无迹Kalman滤波和异步滤波的原理及其Matlab代码的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---