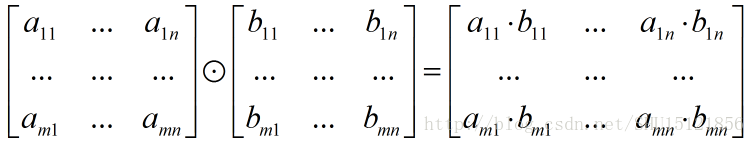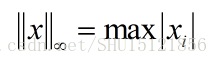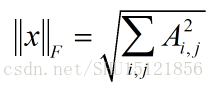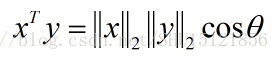本文主要是介绍【ML学习笔记】5:机器学习中的数学基础5(张量,哈达玛积,生成子空间,超平面,范数),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
向量/矩阵/张量
向量
向量可以表示成一维数组,每个分量可以理解为向量所表示的点在空间中坐标的分量。
矩阵
矩阵可以表示成二维数组,上节理解了矩阵可以理解为线性映射在特定基下的一种定量描述。
张量
张量可以表示成任意维的数组,张量是向量概念向更高阶次的推广,向量是一维张量。
但不能把矩阵简单的看成二维张量,张量是几何的,矩阵是代数的。二阶张量和矩阵概念不同,但可以建立联系,矩阵可以描述二阶张量的一些特性(在确定坐标系后,可以用矩阵来表示)。
向量的广播
复制向量到很多位置的操作称为向量的广播,如把m维行向量加到n行m列的矩阵的每一行就是一种广播操作。
向量内积
内积即点积,两个相同维数向量对应分量相乘再相加,得到的是标量,向量x和向量y的内积可以记为:
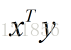
这是因为我们这里说的”向量”可以视为就是在说”列向量”,所以可以看成列向量转置后得到的行向量和另一个列向量的矩阵的标准乘积。
显然向量点积满足交换律。
矩阵的标准乘积
就是普通的矩阵乘法,要求前一个矩阵的列数和后一个矩阵的行数相同,结果矩阵中Cij=左边矩阵的第i行向量和右边矩阵的第j列向量的对应分量相乘再相加。
矩阵的Hadamard乘积
两个规模相同的矩阵,如果对应位置的元素可乘,那么就有Hadamard乘积,新矩阵的规模与原来矩阵的规模一致,每个位置的元素是原来两个矩阵的那个位置元素的乘积。
生成子空间
一组向量的生成(线性)子空间,是它们经过线性组合后所能抵达的点的集合。
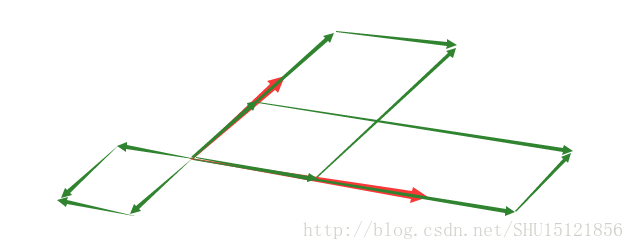
在这张图中,这两个红色的向量经过线性组合,能达到的点构成了一个二维的平面。
超平面
超平面是指n维欧式空间中维度等于n-1的线性子空间,如在三维的欧式空间中就是一个平面,在二维的欧式空间中就是一个点,在更高维的空间中我们生活中找不到描述它的词。
因为是子空间,所以超平面一定过原点。
线性相关和线性无关
如果一组向量中,每个向量都不能表示成其它向量的线性组合,则称这组向量线性无关,否则就是线性相关的,比如下面这三个向量构成的向量组就是线性相关的,因为:
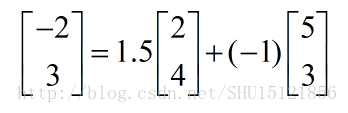
这个向量可以被另外两个向量的线性组合表示,画到图上就是:
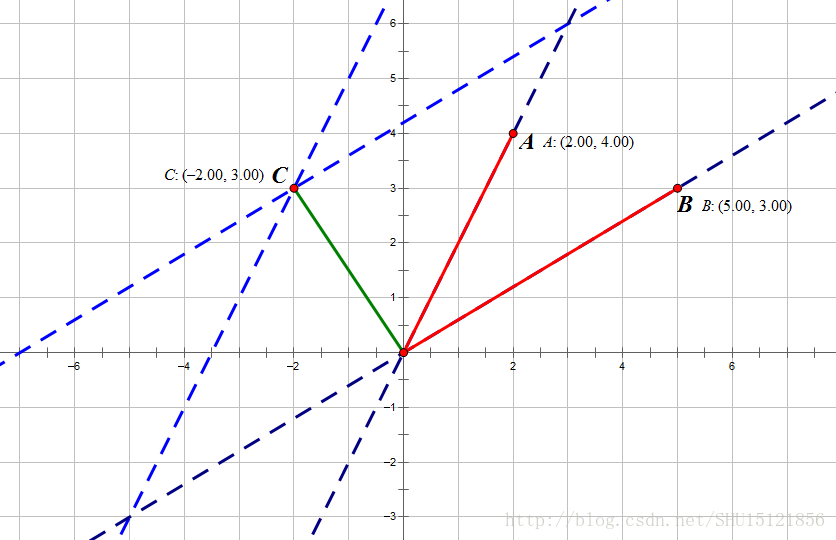
很显然用A和B这两个向量构成的向量组,其生成子空间就是这个整个二维平面了,而加入了这个向量C以后,因为C能被我们之前这个向量组中的向量线性表示,加入了它生成子空间也不会有丝毫的变大,从这个意义上来看,这个能被其它向量线性表示的向量在向量组中是冗余的。
关于逆矩阵
其实只要记住有逆矩阵的一定是一个方阵,并且所有列向量都是线性无关的。但是在书上看到这一部分很有意思,还是做一下笔记。
考虑解一个线性方程组Ax=b,未知的是列向量x:
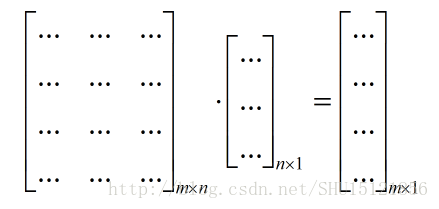
如果矩阵A的逆存在的话,可以试图用A的逆矩阵去求解它,那就要左乘A的逆。对于这个方程组而言,只可能无解/有1个解/有无限多个解,因为如果列向量x1和x2都是这个方程的解,那么对于任意实数α:
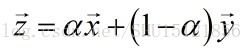
前面学了,矩阵和向量的乘积,可以理解成矩阵的列向量的线性组合,而决定线性组合的权重值的正是这个向量x的每个分量。所以求方程的解,实际上也就是求有哪些种线性组合的方法——x中的第i个分量表示沿着矩阵i的第i列的列向量走多远,能够到达向量b。
所以方程Ax=b有没有解,实际上就是在询问向量b是否在矩阵A的列向量的生成子空间中,如果在的话,x的分量描述了到达这个向量b的途径。这个特殊的生成子空间称为矩阵A的列空间或者值域。
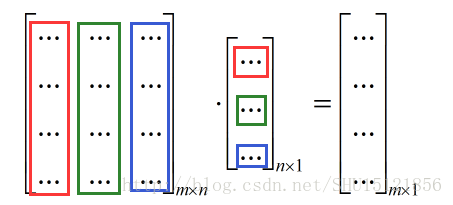
如果要对任意m维向量b都存在解,就要使矩阵A的列空间布满整个m维空间,所以A至少要有m列,否则其线性组合是不可能达到m维的,如一个3x2的矩阵(m=3而n=2):
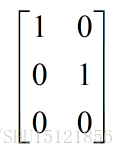
很显然这两个3维列向量不论怎么组合,都只能在一个平面上跑,也就是说这个矩阵的列空间只能是一个平面,而不能包括m=3维度上的所有点。
回到那个问题,A至少有m列也就是n>=m。这只是一个必要条件,还不是充分条件,因为有些列可能是多余的,如下面这个矩阵:
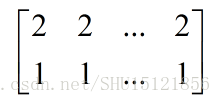
很显然不管有再多的列,因为列都是一样的,不管列向量再怎么组合,都只能在一条直线上跑,不能包括m=2维度上的所有点。这种多余就是因为这些列向量线性相关了。
所以要使列向量线性组合后能包含整个m维空间上的所有点,就要求这个矩阵的列至少有一组m个线性无关的向量,用它们就能实现包括m维度上的所有点了,也就是m维线性空间中的一组基。
要用逆矩阵来求的话,左乘逆矩阵以后得到的x肯定是唯一的,所以要保证方程对于每一个b最多只能有一个解,那么矩阵就最多只能有m个列向量。这是因为如果有多于m个列向量,又有了前面说了m个线性无关的向量,那么剩下的那个向量肯定能被这m个向量线性表示,那么它就能替代线性表示它的向量中的任意一个:

上图中红色是一个m个向量的线性无关组,蓝色是表示绿的向量的一组向量(权重不是0),绿色的这个向量可以去替代这个线性无关组中的蓝色向量中的任意一个,而新的组仍然是m个向量的线性无关组。
那么有了多种线性无关组m,就会有不止一种线性组合:
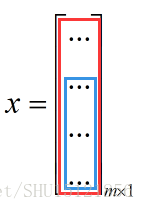
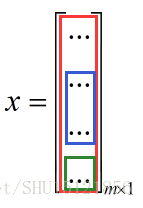
该方程也就有不止一个解x了,因此n<=m。
综上来看n=m,也就是矩阵A需要是个方阵,而且列向量线性无关,这样才可逆,可逆矩阵也叫非奇异矩阵。此外,列向量线性相关的方阵被称为奇异矩阵。
根据前面说的线性相关和线性无关可以理解:如果A为奇异矩阵,则AX=0有无穷解(能被线性表示的列向量线性表示后,权重可以同乘任意实数),AX=b有无穷解或者无解(如果b不能被A的列向量线性表示就无解,否则有无穷多解,无穷的方式还是那一个解的1-α权重组合)。如果A为非奇异矩阵,则AX=0有且只有唯一零解(m维的0向量b自然也是有唯一解,这个解总是m=n维0向量因为列向量谁们也不能表示谁),AX=b有唯一解(正如前面所说)。
范数
范数(norm)可以衡量向量的大小,向量x的范数可以衡量从原点到x点的距离,显然这个距离和我们平时生活中的距离不太一样。
范数的性质
①正定性:如果向量x的范数为0,向量一定是0向量。
②三角不等式:两向量和的范数不大于范数之和。
③正值齐次性:缩放α倍后的x的范数等于x的范数乘以α的绝对值。
Lp范数
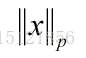
展开的分量的p次幂加和再开p次方,即:
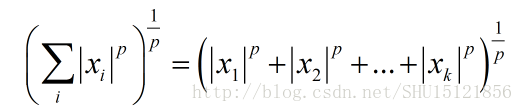
显然L2范数表示的就是从原点到指定点的欧几里徳距离,这个距离也就是我们日常生活说的狭义的距离,L2范数也叫欧几里徳范数。
L1范数是x的所有分量的单纯加和,当机器学习问题中零和非零的元素差异很重要时通常使用L1范数(书上这样说,但具体怎么用还是不清楚)。
最大范数(L∞范数)
取向量中具有最大幅值的元素的绝对值:
Frobenius范数
用来衡量矩阵的大小,矩阵中每个元素平方后全部加起来再开根号:
用L2范数表示向量点积
高中学的”模乘模乘夹角余弦”里的”模”其实就是向量的L2范数:
这篇关于【ML学习笔记】5:机器学习中的数学基础5(张量,哈达玛积,生成子空间,超平面,范数)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!