本文主要是介绍多段图问题-动态规划解法,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、多段图问题
问题描述:设图G=(V, E)是一个带权有向图,如果把顶点集合V划分成k个互不相交的子集Vi (2≤k≤n, 1≤i≤k),使得对于E中的任何一条边(u, v),必有u∈Vi,v∈Vi+m (1≤i≤k, 1<i+m≤k),则称图G为多段图,称s∈V1为源点,t∈Vk为终点。多段图的最短路径问题求从源点到终点的最小代价路径。
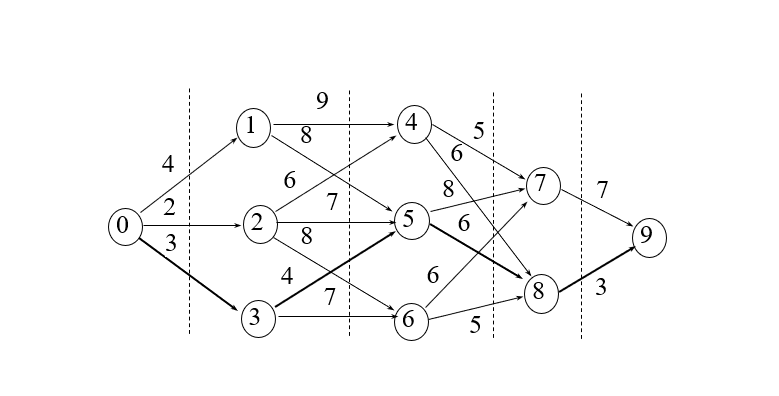
二、抽象分析
设Cu-v表示多段图的有向边<u, v>上的权值,将从源点s到终点t的最短路径长度记为d(s, t),考虑原问题的部分解d(s, v),显然有下式成立:
d(s, v) =Cs-v (<s, v>∈E)
d(s, v) = min{d(s, u) + Cu-v} (<u, v>∈E)
1.循环变量j从1~n-1重复下述操作,执行填表工作
1.1考察顶点j的所有入边,对于边<i,j>∈E,执行下述操作
1.1.1cost[j]=min{cost[i]+c[i][j]};
1.1.2path[j]=使cost[i]+c[i][j]最小的i;
1.2 j++;
2.输出最短路径长度cost[n-1];
3.循环变量i=path[n-1].循环直到path[i]=0,输出最短路径经过的顶点;
3.1 输出path[i];
3.2 i=path[i]
三、例题具体分析
首先求解初始子问题,可直接获得:
d(0, 1)=c01=4(0→1)
d(0, 2)=c02=2(0→2)
d(0, 3)=c03=3(0→3)
再求解下一个阶段的子问题,有:
d(0, 4)=min{d(0, 1)+c14, d(0, 2)+c24}=min{4+9, 2+6}=8(2→4)
d(0, 5)=min{d(0, 1)+c15, d(0, 2)+c25, d(0, 3)+c35}=min{4+8, 2+7, 3+4}
=7(3→5)
d(0, 6)=min{d(0, 2)+c26, d(0, 3)+c36}=min{2+8, 3+7}=10(2→6)
再求解下一个阶段的子问题,有:
d(0, 7)=min{d(0, 4)+c47, d(0, 5)+c57, d(0, 6)+c67}=min{8+5, 7+8, 10+6}
=13(4→7)
d(0, 8)=min{d(0, 4)+c48, d(0, 5)+c58, d(0, 6)+c68}=min{8+6, 7+6, 10+5}
=13(5→8)
直到最后一个阶段,有:
d(0, 9)=min{d(0, 7)+c79, d(0, 8)+c89}=min{13+7, 13+3}=16(8→9)
再将状态进行回溯,得到最短路径0→3→5→8→9,最短路径长度16。
(附输入)
10 18
0 1 4
0 2 2
0 3 3
1 4 9
1 5 8
2 4 6
2 5 7
2 6 8
3 5 4
3 6 7
4 7 5
4 8 6
5 7 8
5 8 6
6 7 6
6 8 5
7 9 5
8 9 3四、代码
#include<iostream>
using namespace std;int vnum, arcnum;
int arc[100][100];
const int INT_MAX1 = 999;void printArc()
{cout << "邻接矩阵为:" << endl;for (int i = 0; i < vnum; i++){for (int j = 0; j < vnum; j++){cout << arc[i][j] <<" ";}cout << endl;}cout << endl;
}int main()
{cin >> vnum >> arcnum;int i, j;//初始化邻接矩阵,用999表示没有边for (i = 0; i < vnum; i++){for (j = 0; j < vnum; j++){arc[i][j] = INT_MAX1;}}printArc();//输入各边while (arcnum--){int weight;cin >> i >> j >> weight;arc[i][j] = weight;}printArc();int cost[100] = { 0 };//记录最小的代价int path[100] = { 0 };//记录路径,即经过的顶点//初始化for (i = 1; i < vnum; i++){cost[i] = INT_MAX;path[i] = -1;}cost[0] = 0;path[0] = -1;//开始动态规划,找出最小代价for (j = 1; j < vnum; j++){for (i = j - 1; i >= 0; i--){if (cost[i] + arc[i][j] < cost[j]){cost[j] = cost[i] + arc[i][j];path[j] = i;}}}// 输出路径i = vnum - 1;cout << i;while (path[i] >= 0) { // 前一个点大于0 cout << "<-" << path[i];i = path[i]; // 更新为前一个点 }cout << endl;cout << "最短路径为:" << cost[vnum -1] << endl;system("pause");return 0;
}这篇关于多段图问题-动态规划解法的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







