本文主要是介绍c 语言 堆的解析(自我理解)!!!堆排序,建堆,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
1.堆是什么?
首先先看一个图片

小顶堆的意思就是顶 的元素最小,两个子节点的元素要大于父节点。大顶堆同理。
小顶堆就像是一个金字塔。第一层很小,然后后面是依次增大,就像社会人才金字塔图一样。
大顶堆就可以想做,每个人的财富拥有值的金字塔图,上层人的钱很多,而底层的人钱最少。
其次关于堆,其实堆在通常情况下是一个完全二叉树 (只有最底层的节点没有充满的二叉树,全充满的也属于完全二叉树叫做满二叉树)

那堆能干嘛呢,首先堆是可以用来排序的,而且排序的时间也是较快,处于(n*logn)这个层级。
还有一个就是在频繁的出队和入队时,用堆是一个不错的选择。如果用数组和链表来完成pop和push时,时间复杂度是O(n)而用 堆就是O(log n)。
在一个堆中通常用parent 和 child 来表示父节点和子节点。堆通常都是用数组来实现的。
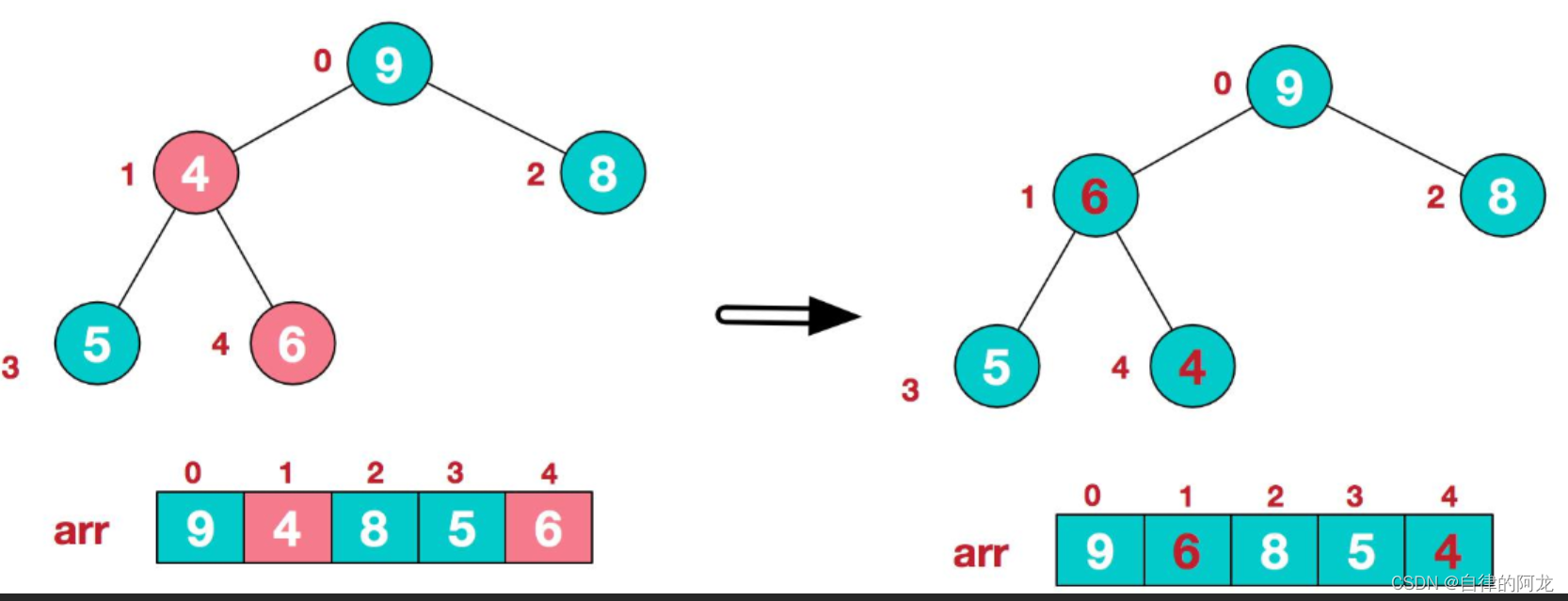
通过上图可以看出堆的父节点如果为0的话,子节点就是1 和 2.就可以推导出公式
child = parent * 2 +1 或者 parent * 2 + 2。parent = child / 2。
2.堆的实现和接口。(小堆)
1.头文件
#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
#include<time.h>
typedef int HPDataType;
typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;
void Swap(int* C, int* P);
void AdjustUP(int* a, int size);//向上调整
void AdjustDown(HPDataType* a, int size,int parent);//向下调整
void HPInit(HP* hp);//初始化
void HPDestroy(HP* hp);//摧毁
void HeapPush(HP* hp, HPDataType x);//加入数据
void HeapPop(HP* hp);//删除数据
HPDataType HeapTop(HP* hp);//查找头元素
int HeapSize(HP* hp);//有效元素个数
bool HeapEmpty(HP* hp);//判空堆的底层和顺序表的底层很像,但二者也不是相同。
size 的意思是目前元素的个数
capacity是当前开辟的空间的容量
2.初始化
void HPInit(HP* hp)
{assert(hp);hp->a = NULL;hp->capacity = 0;hp->size = 0;
}3.摧毁
void HPDestroy(HP* hp)
{assert(hp);free(hp->a);hp->a = NULL;hp->capacity = 0;hp->size = 0;
}4.向上调整(重点)
void AdjustUP(int* a,int Child)
{assert(a);int Parent = (Child - 1) / 2;while (Child > 0){if (a[Child] < a[Parent]){Swap(&(a[Child]), &(a[Parent]));}else{break;}Child = (Child - 1) / 2;Parent = (Parent - 1) / 2;}
}关于向上调整实际上就是,把选定的Child位置元素,以大堆或小堆的方式向上调整。
因为向上调整是从孩子的位置开始向父亲的位置开始调整的,因为向上嘛,如果是父亲调儿子辈分就乱了。所以传入进来的 child 。然后 child > 0 ,是为了让 最后 孩子走到顶就是 0 的位置以后 这时才将所有的父节点比较结束。
因为实现的是小堆,如果子节点的值小于父节点就交换二者的值。出现 大于父节点的值就break。child = (child - 1)/2 是为了让子节点成为父节点,而 parent = (parent - 1)/2是为了让父节点等与下一个父节点,大致想象为爷爷节点。
5.向下调整(重点)
void AdjustDown(HPDataType *a,int size,int parent)
{assert(a);int child = parent*2+1;while (child < size){if (child + 1 < size && a[child] > a[child + 1]){++child;}if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}顾名思义 向下调整就是以开头第一个元素为始,开始依次向子节点比较,当child 大于或等于size时循环停止,child + 1小于size 和 a【child】 大于 a【child + 1】条件的原因是,因为向下调整要对比的是两个子节点,通过比较 选出较小的节点(小堆),如果 【child+1】较小就++child。如果父节点比最小的子节点大,那就交换二者的位置,然后向下以这个逻辑,循环到如果出现 最小的孩子 比父亲节点还大的话,那就break循环,如果没有就循环到child大于等于size为止。
6.插入(重点)
void HeapPush(HP* hp, HPDataType x)
{assert(hp);if (hp->capacity == hp->size){int newcapacity = hp->capacity == 0 ? 4 : 2 * hp->capacity;HPDataType* tmp = (HPDataType*)realloc(hp->a,sizeof(HPDataType) * newcapacity);if (tmp == NULL){perror("realloc failed");exit(-1);}hp->a = tmp;hp->capacity = newcapacity;}hp->a[hp->size] = x;hp->size++;AdjustUP(hp->a,hp->size);
}对于堆的插入呢,当然首先也是尾插,因为这是一个小堆,如果你插入一个特别小的数,那么这个堆就得重新开始调整了。当然调整就用一个向上调整即可,从最下面往上面调整。
因为是插入,所以要先判断整个数列的空间和现在的元素个数,如果 相等了那就得扩容了。
扩容好以后,把要插入的数字尾插在数列的尾端,同时size++,然后对这个数字进行向上调整。
7.删除(重点)
void HeapPop(HP* hp)
{assert(hp);Swap(&(hp->a[hp->size]), &(hp->a[0]));hp->size--;AdjustDown(hp->a,hp->size,0);
}堆的删除,不是尾删 。而是把头元素删除。
所以一般的堆删除就是把头尾交换,在把size-- 和顺序的删除很像,就是删除的头结点。、
删除之后对堆在进行一次向下调整即可。因为传上来的数字本来就是在最下面的,所以要把它在沉到最下面。
8.头元素
HPDataType HeapTop(HP* hp)
{assert(hp);return hp->a[0];
}9.元素个数
int HeapSize(HP* hp)
{assert(hp);return hp->size;
}10.判空
bool HeapEmpty(HP* hp)
{assert(hp);return hp->size == 0;
}3.堆的排序。
所谓排序,相信大家都已经学过冒泡排序了把,排序就是把一串数字排成升序或者降序。
那我们为什么要学习排序呢?最重要的一点就是 面试 sdad
在笔试的时候,最主要的就是靠算法题。像拼多多、头条这种大公司,上来就来几道算法题,如果你没AC出来,面试机会都没有。
在面试(现场面或者视频面)的时候也会问算法题,难度肯定是没有笔试的时候那么难的。我们可以想象一个场景,一面面试面到一半,面试官让你反转二叉树,问问现在的自己,你还会吗。
所以这些排序我们都还得学,当然以后如果有这方面的工作也会用得到,技多不压身。
堆排序的源代码和实现
#include"Heap.h"
void HeapSort(int* a, size_t size)
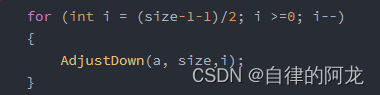
{for (int i = (size-1-1)/2; i >=0; i--){AdjustDown(a, size,i);}for (int i = size-1; i > 0; i--){Swap(&a[i], &a[0]);AdjustDown(a, i,0);}
}
int main()
{int arr[] = { 4,10,22,3,6,9,25,11,715 };HeapSort(arr, sizeof(arr) / sizeof(arr[0]));return 0;
}首先堆排序咱有两步,第一步是先把一组数组先把它先建立成堆。
第二步就是用调整的方法把这个数组变成有序的
关于建堆有两种方法,第一种是用向上调整直接从数组第一个开始,每一个都进行一次向上调整,如果这样调整的话,建堆这个过程的时间复杂度就是n * logn。
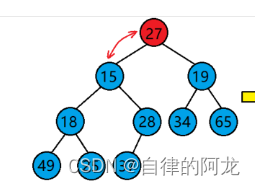
而向下调整建堆的时间复杂度则到达了 n ,快了很多,这是向下调整的图片
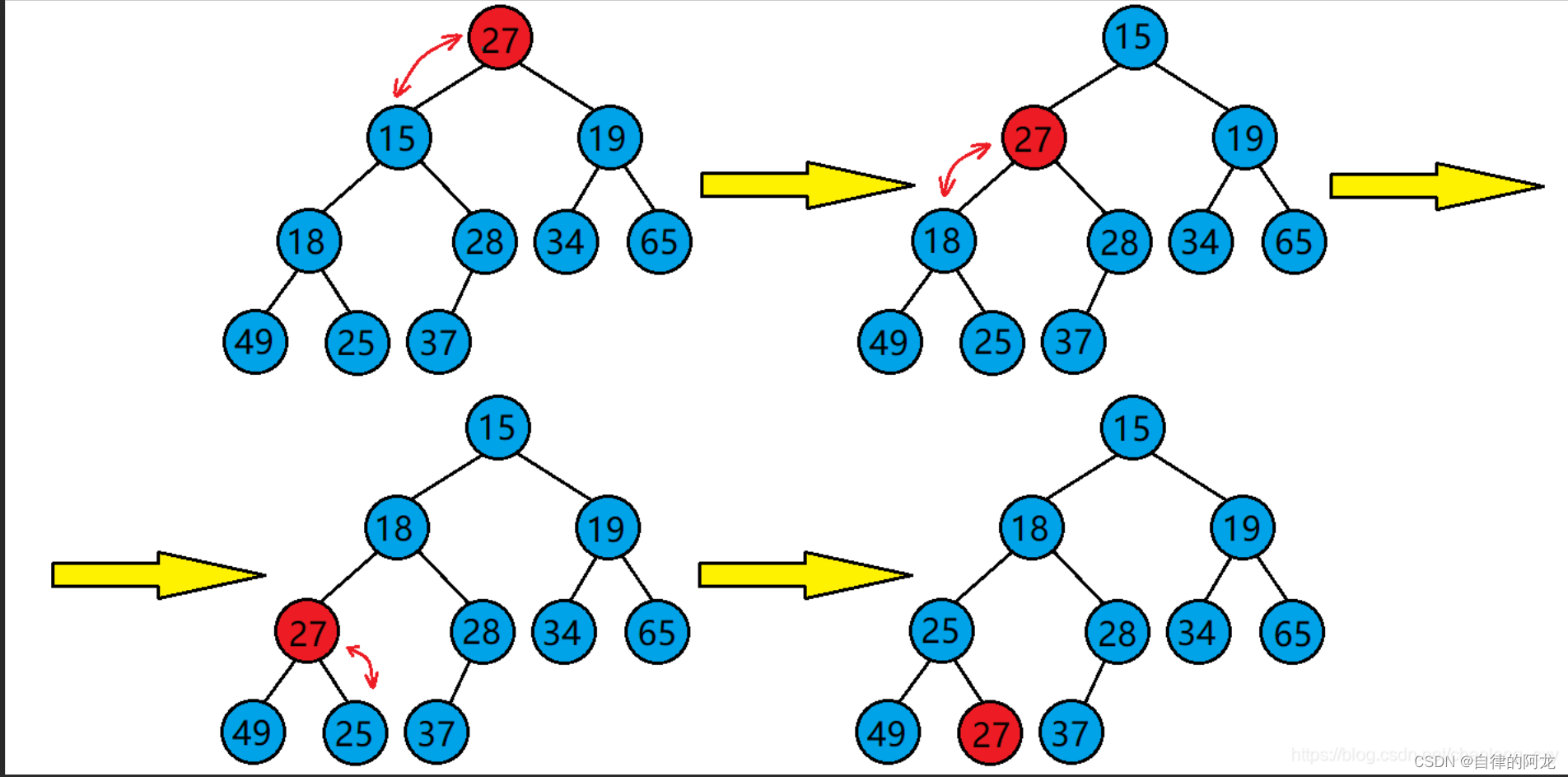
而我们用向下调整建堆呢,是从这个图元素大小为28的最后一个元素的父节点来进行调整的,这种建堆的关键就是从倒数第一个非叶子节点开始调(也就是树中最后一个父节点),然后逐渐+1,就可以调整从最后一个父节点开始的每一棵树.公式里的第一个size - 1呢是因为本来size是计算元素个数的,数组又是从0开始排序的,所以size - 1是要得到最后一个叶子结点。
而第二个 - 1呢是因为,parent = (child - 1)/ 2.因为adjustdown中传入的第三个变量是parent 所以 需要第二次 - 1.(所以一般建堆都是用向下调整建堆,时间效率高)
这篇关于c 语言 堆的解析(自我理解)!!!堆排序,建堆的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





