[足式机器人]Part2 Dr. CAN学习笔记-数学基础Ch0-4线性时不变系统中的冲激响应与卷积

本文主要是介绍[足式机器人]Part2 Dr. CAN学习笔记-数学基础Ch0-4线性时不变系统中的冲激响应与卷积，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

本文仅供学习使用
本文参考：
B站：DR_CAN

---

线性时不变系统 ： LIT System
冲激响应：Impluse Response
卷积：Convolution

1. LIT System：Linear Time Invariant

• 运算operator : O { ⋅ } O\left\{ \cdot \right\} O{⋅}
  I n p u t O { f ( t ) } = o u t p u t x ( t ) \begin{array}{c} Input\\ O\left\{ f\left( t \right) \right\}\\ \end{array}=\begin{array}{c} output\\ x\left( t \right)\\ \end{array} InputO{f(t)}​=outputx(t)​

• 线性——叠加原理superpositin principle：
  { O { f 1 ( t ) + f 2 ( t ) } = x 1 ( t ) + x 2 ( t ) O { a f 1 ( t ) } = a x 1 ( t ) O { a 1 f 1 ( t ) + a 2 f 2 ( t ) } = a 1 x 1 ( t ) + a 2 x 2 ( t ) \begin{cases} O\left\{ f_1\left( t \right) +f_2\left( t \right) \right\} =x_1\left( t \right) +x_2\left( t \right)\\ O\left\{ af_1\left( t \right) \right\} =ax_1\left( t \right)\\ O\left\{ a_1f_1\left( t \right) +a_2f_2\left( t \right) \right\} =a_1x_1\left( t \right) +a_2x_2\left( t \right)\\ \end{cases} ⎩ ⎨ ⎧​O{f1​(t)+f2​(t)}=x1​(t)+x2​(t)O{af1​(t)}=ax1​(t)O{a1​f1​(t)+a2​f2​(t)}=a1​x1​(t)+a2​x2​(t)​

• 时不变Time Invariant：
  O { f ( t ) } = x ( t ) ⇒ O { f ( t − τ ) } = x ( t − τ ) O\left\{ f\left( t \right) \right\} =x\left( t \right) \Rightarrow O\left\{ f\left( t-\tau \right) \right\} =x\left( t-\tau \right) O{f(t)}=x(t)⇒O{f(t−τ)}=x(t−τ)

2. 卷积 Convolution

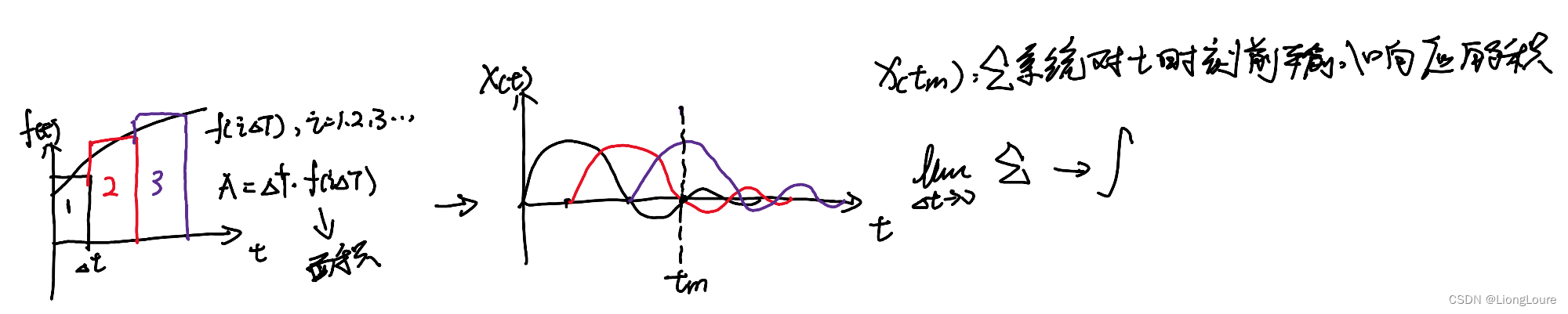
3. 单位冲激 Unit Impulse——Dirac Delta

LIT系统，h(t)可以完全定义系统

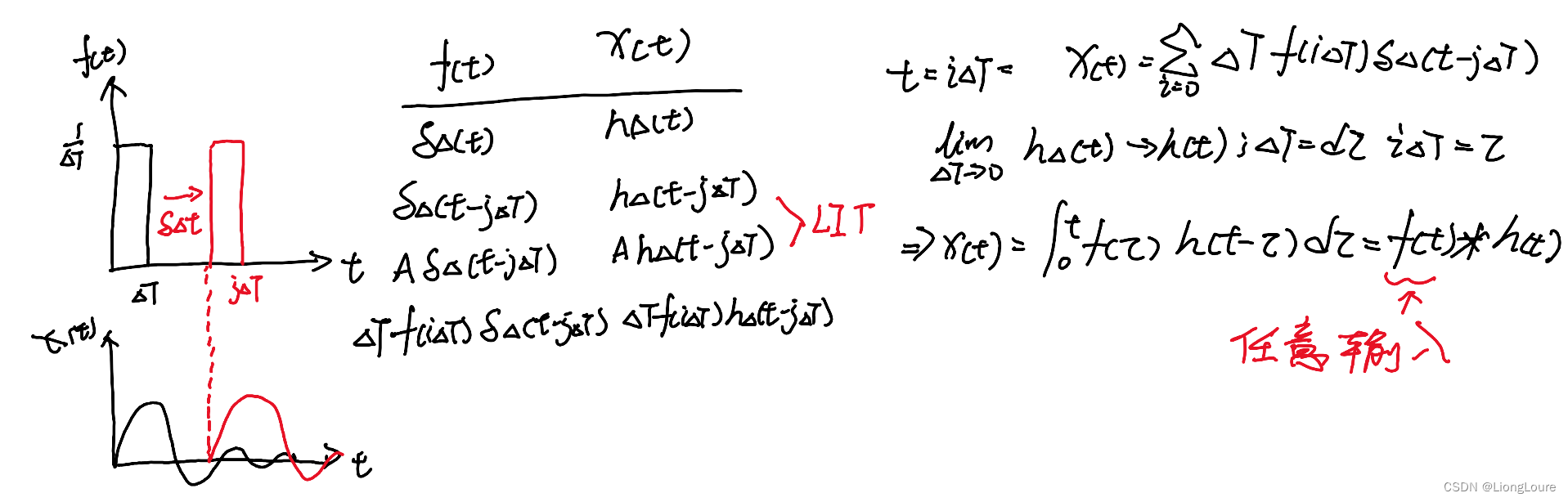
这篇关于[足式机器人]Part2 Dr. CAN学习笔记-数学基础Ch0-4线性时不变系统中的冲激响应与卷积的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---