本文主要是介绍台湾国立大学郭彦甫Matlab教程笔记(18) root finding(symbolic),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
today:
symbolic approach 运用符号的方式求根
numeric root solvers数值的方式求根
recursive functions 递归函数
problem statement问题陈述
suppose you have a mathematical function f(x) and you want to finx x0 such that f(x0)=0,e.g.
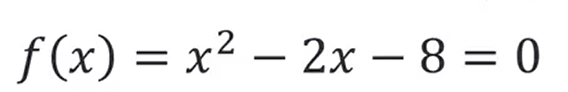
how do you solve the problem using MATLAB?
analytical solutions 解析解,求根公式
graphical illstration图形描述
numerical solutions 数值解
今天focus analytical solution and numerical sulution
symbolic root finding approach 符号方法
performing mathematics on symbols ,not numbers 把数值变成 symbol符号形式
the symbols math are performed using 'symbolic varibles’符号变量
怎么做呢?
use sym or syms to create symbolic varibles
举例:如何把x宣告成 symbolic 的形式
syms x%x变成 symbolic varible
x+x+x
(x+x+x)/4
运行结果可以看到:

还有一个指令
x=sym(‘x’);
下面要定义一个函数,用symbolic 的形式
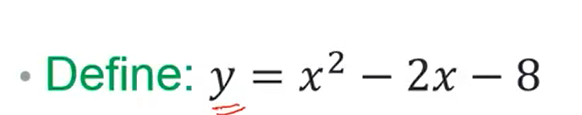
运行结果:
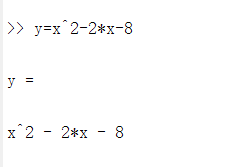
现在知道了 symbolic varible ,就要用symbolic 的方式解决方程式求根的问题
symbolic root finding :solve()符号法求根
function : solve finds roots for equations
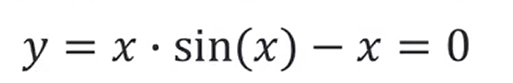
如何用matlab来求解呢?
第一步,需要让x变成 symbolic varible
第二步,y表示出来
第三步solve(y,x)参数是方程在前,自变量在后面
例程代码:
syms x;
y=x*sin(x)-x;
solve(y,x)%solve 直接让y=0,不用手动再令成零。得到上面方程的根:
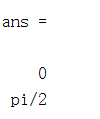
需要注意的是,这个结果ans 也是symbolic variable 不是数值变量
练习题:

我的练习:
syms x;
y=(cos(x)).^2-(sin(x).^2);
solve(y,x)
运行结果:得到第一个方程的根是 pi/4

第二题:
代码:
syms x;
y=(cos(x)).^2+(sin(x)).^2;
solve(y,x)
执行结果发现这个方程无解。根据高中的知识,确实y=1,不会等于0

下一个问题
solving multiple equations多个方程求解
只需要多声明symbolic varibles
例题:解二元一次方程组

例程代码:
syms x y;
eq1=x-2*y-5;
eq2=x+y-6;
A=solve(eq1,eq2,x,y)%两个方程放在前面运行上面代码,我们就解出来这个方程组:但是得到的是一个structure,

如何显示structure中的元素呢?
A.x
A.y
得到方程组的解:

再来看下一个问题
solving equations expressed in symbols解带符号的方程
举例:
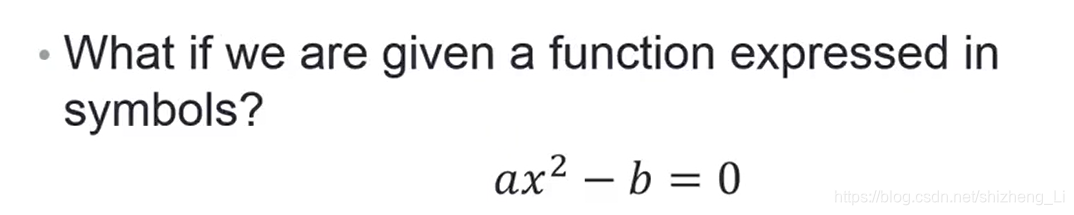
例程代码:(新版matlab运行不了)
syms x a b
solve('a*x^2-b')
执行时出现错误:

好像不能这样用(solve()里面方程用单引号‘’好像已经不能这样来处理了)

换一种写法试试
syms x a b;
y=a*x^2-b;
solve(y,x)
发现行得通,运行结果得到用a和b表示的方程的解

上面这个例题中x是未知数,如果让b是未知数,a和x是已知,我们怎么解呢?
x is always the first choice to be solved,一般x是默认的未知数
what if one wants to express b in terms of a and x?
如果想要b是未知数的话,需要改变一下指令
如下程序:(代码有问题)
syms x a b
y=a*x^2-b;
solve(y,'b')%意思是b是 unknown 未知的
发现这段代码出现错误:

改正:b不需要加单引号。就像solve(y,x)一样,x是未知数。
代码:
syms x a b
y=a*x^2-b;
solve(y,b)%意思是b是 unknown 未知的
得到结果:用x和a表示出来的b

练习题:

第一个题目:用symbolic 的方式求解一个圆的方程,其中只把x当作未知数
第二个题目:用符号的方法求一个矩阵的逆矩阵(matrix inverse)
思路:需要把a,b,c,d声明成 syms,同时需要一个求逆矩阵的指令,老师讲好像是inv()
我的练习:
第一题代码:
syms x y a b r;
f=(x-a).^2+(y-b).^2-r.^2;%方程
solve(f,x)%求解根
计算结果:

第二题解决:
先查一查inv()函数是何方神圣,发现inv()确实可以求逆矩阵

syms a b c d;
A=[a,b;c,d];%用symbolic 形式表示的矩阵
inv(A)%求逆矩阵的指令
运行结果,得到A矩阵的逆矩阵

【总结一下】
本文学习了方程求根的一中方法,用symbolic 的方法,可以显式的表达出来一个结果,很直观。
声明符号变量使用 关键字 syms
求根使用函数solve()
解方程组 也可以使用solve()函数,只需要加上几个形参。
同样可以解带有a,b等字母系数的方程
这篇关于台湾国立大学郭彦甫Matlab教程笔记(18) root finding(symbolic)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








