LeetCode：2646. 最小化旅行的价格总和（dfs + 树形dp C++、Java)

本文主要是介绍LeetCode：2646. 最小化旅行的价格总和（dfs + 树形dp C++、Java)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

2646. 最小化旅行的价格总和

题目描述：

实现代码与解析：

DFS + DP

原理思路：

---

2646. 最小化旅行的价格总和

题目描述：

        现有一棵无向、无根的树，树中有 n 个节点，按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。

每个节点都关联一个价格。给你一个整数数组 price ，其中 price[i] 是第 i 个节点的价格。

给定路径的 价格总和 是该路径上所有节点的价格之和。

另给你一个二维整数数组 trips ，其中 trips[i] = [starti, endi] 表示您从节点 starti 开始第 i 次旅行，并通过任何你喜欢的路径前往节点 endi 。

在执行第一次旅行之前，你可以选择一些 非相邻节点 并将价格减半。

返回执行所有旅行的最小价格总和。

示例 1：

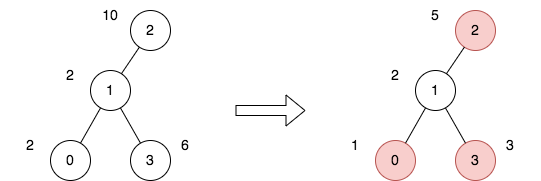
输入：n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]
输出：23
解释：
上图表示将节点 2 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 、2 和 3 并使其价格减半后的树。
第 1 次旅行，选择路径 [0,1,3] 。路径的价格总和为 1 + 2 + 3 = 6 。
第 2 次旅行，选择路径 [2,1] 。路径的价格总和为 2 + 5 = 7 。
第 3 次旅行，选择路径 [2,1,3] 。路径的价格总和为 5 + 2 + 3 = 10 。
所有旅行的价格总和为 6 + 7 + 10 = 23 。可以证明，23 是可以实现的最小答案。

示例 2：

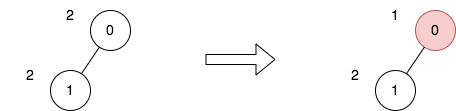
输入：n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]
输出：1
解释：
上图表示将节点 0 视为根之后的树结构。第一个图表示初始树，第二个图表示选择节点 0 并使其价格减半后的树。 
第 1 次旅行，选择路径 [0] 。路径的价格总和为 1 。 
所有旅行的价格总和为 1 。可以证明，1 是可以实现的最小答案。

提示：

• 1 <= n <= 50
• edges.length == n - 1
• 0 <= ai, bi <= n - 1
• edges 表示一棵有效的树
• price.length == n
• price[i] 是一个偶数
• 1 <= price[i] <= 1000
• 1 <= trips.length <= 100
• 0 <= starti, endi <= n - 1

实现代码与解析：

DFS + DP

C++

class Solution {
public:int N = 50 + 10;vector<int> e = vector<int>(N * 2, 0), ne = vector<int>(N * 2, 0), h = vector<int>(N, -1);vector<int> cnt = vector<int>(N, 0);int idx= 0;// 邻接表加边 void add(int a, int b) {e[idx] = b; ne[idx] = h[a]; h[a] = idx++;}bool dfs(int cur, int p, int end) {if (cur == end) {cnt[cur]++;return true;}for (int i = h[cur]; ~i; i = ne[i]) {int j = e[i];if (j == p) continue;if (dfs(j, cur, end)) {cnt[cur]++;return true;}}return false;}// first，当前节点不减半可以获得的最小金额，second，当前节点减半pair<int, int> dpf(int cur, int p, vector<int> price) {pair<int, int> res = {price[cur] * cnt[cur], price[cur] * cnt[cur] / 2};for (int i = h[cur]; ~i; i = ne[i]) {int j = e[i];if (j == p) continue;pair<int, int> t = dpf(j, cur, price);res.first += min(t.first, t.second); // 当前节点不减半，那么孩子可减半，也可不减取最大res.second += t.first; // 当前节点减半，子节点一定不能减半}return res;}int minimumTotalPrice(int n, vector<vector<int>>& edges, vector<int>& price, vector<vector<int>>& trips) {// 初始化图for (auto e: edges) {add(e[0], e[1]);add(e[1], e[0]);}// dfsfor (auto t: trips) {dfs(t[0], -1, t[1]);}auto [x, y] = dpf(0, -1, price);return min(x, y); // 取最小}
};

Java

class Solution {public int N = 50 + 10;public int[] e = new int[N * 2], ne = new int[N * 2], h = new int[N];public int[] cnt = new int[N];public int idx = 0;public void add(int a, int b) {e[idx] = b; ne[idx] = h[a]; h[a] = idx++;}public boolean dfs(int cur, int p, int end) {if (cur == end) {cnt[cur]++;return true;}for (int i = h[cur]; i != -1; i = ne[i]) {int j = e[i];if (j == p) continue;if (dfs(j, cur, end)) {cnt[cur]++;return true;}}return false;}public int[] dp(int cur, int p, int[] price) {int[] res = {price[cur] * cnt[cur], price[cur] * cnt[cur] / 2};for (int i = h[cur]; i != -1; i = ne[i]) {int j = e[i];if (j == p) continue;int[] t = dp(j, cur, price);res[0] += Math.min(t[0], t[1]);res[1] += t[0];}return res;}public int minimumTotalPrice(int n, int[][] edges, int[] price, int[][] trips) {Arrays.fill(h, -1);for (int[] t: edges) {add(t[0], t[1]);add(t[1], t[0]);}for (int[] t: trips) {dfs(t[0], -1, t[1]);}int[] res = dp(0, -1, price);return Math.min(res[0], res[1]);}
}

原理思路：

        此题，可以拆分为两道题，DFS + 树形DP。

dp之前先用dfs遍历处理一下，找出每个节点总共经过的次数。

dp返回数组的含义和递推式：

        res[0]表示，此节点不减半可获得的最小值，此节点不减半，那么其孩子节点就可减半，可不减半，取最小min。res[0] += min(childres[0], childres[1]); // 这里用childres来表示孩子返回值解释

        res[1]表示，此节点减半可获取的最小值，此节点减半，那么其孩子节点就一定不能减半，直接加上孩子返回的不减半值即可。 res[1] += childres[0];

和树形的 打家劫舍III 思路相同，只不过那题是取最大值。

Leetcode每日一题：打家劫舍系列Ⅰ、Ⅱ、Ⅲ、Ⅳ（2023.9.16~2023.9.19 C++）_Cosmoshhhyyy的博客-CSDN博客

这篇关于LeetCode：2646. 最小化旅行的价格总和（dfs + 树形dp C++、Java)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---