【组合数学】容斥鸽巢原理

本文主要是介绍【组合数学】容斥鸽巢原理，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 容斥原理

容斥原理提供了一种通过计算每个单独集合的大小，然后修正重复计数的方法，从而得到多个集合并集大小的计算方法。它通过减去每个交集的元素个数，再加上每两个集合的交集，再减去每三个集合的交集，以此类推，来避免多重计数。

定理 1.1：容斥原理$$\left|\bigcup _{i=1}^n{A}_i\right|=\sum _{k=1}^n(-1{)}^{k-1}\left(\sum _{\begin{array}{c}1\le i_1<i_2<\dots <i_k\le n\end{array}}\left|A_{i_1}\cap A_{i_2}\cap \dots \cap A_{i_k}\right|\right)$$其中$\left|{\bigcup }_{i=1}^n{A}_i\right|$ 表示所有集合的并集中元素的总个数。右侧的求和符号涉及不同交集大小的情况，通过交替加减不同交集的元素个数来计算最终的并集大小。

容斥原理三种形式

定理 1.2： S 是一有限集合，P1, P2,…, Pm 是同集合 S 有关的 m 个性质，设$A_i$是 S 中具有性质 Pi 的元素构成的集合(1 ≤ i ≤ m)，$\overline{A_i}$ 是 S 中不具有性质 Pi 的元素构成的集合(1 ≤ i ≤ m)，则 S 中不具有性质 Pi 的元素的个数为 ∣ A 1 ‾ ∩ A 2 ‾ ∩ . . . ∩ A m ‾ ∣ = ∣ S ∣ − ∑ i = 1 m ∣ A i ∣ + ∑ { 1 , 2 , . . m } 的 2 组合 ∣ A i ∩ A j ∣ − ∑ { 1 , 2 , . . m } 的 3 组合 ∣ A i ∩ A j ∩ A k ∣ + . . . + ( − 1 ) m ∣ A 1 ∩ A 2 ∩ . . . ∩ A m ∣ |\overline{A_1}\cap\overline{A_2}\cap...\cap\overline{A_m}|=|S|-\sum_{i=1}^m|A_i|+\sum_{\{1,2,..m\}的2组合} |A_i\cap A_j|-\\\sum_{\{1,2,..m\}的3组合} |A_i\cap A_j \cap A_k|+...+(-1)^m|A_1\cap A_2 \cap...\cap A_m| ∣A1​​∩A2​​∩...∩Am​​∣=∣S∣−i=1∑m​∣Ai​∣+{1,2,..m}的2组合∑​∣Ai​∩Aj​∣−{1,2,..m}的3组合∑​∣Ai​∩Aj​∩Ak​∣+...+(−1)m∣A1​∩A2​∩...∩Am​∣

习题1、求不超过 120 的素数的个数
解: 因 $11^2$ = 121，故不超过 120 的合数必然是 2，3，5，7 的倍数，而且不超过 120 的合数的因子不可能超过 11 。设 $A_i$ 为不超过 120 的数 i 的倍数的集合(i = 2, 3, 5, 7)则
$$\begin{gathered} |A2|=\lfloor 120/2\rfloor =60,|A3|=\lfloor 120/3\rfloor =40, \\ |A5|=\lfloor 120/5\rfloor =24,|A7|=\lfloor 120/7\rfloor =17, \\ |A2\cap A3|=\lfloor 120/6\rfloor =20,|A2\cap A5|=\lfloor 120/10\rfloor =12, \\ |A2\cap A7|=\lfloor 120/14\rfloor =8,|A3\cap A5|=\lfloor 120/15\rfloor =8, \\ |A3\cap A7|=\lfloor 120/21\rfloor =5,|A5\cap A7|=\lfloor 120/35\rfloor =3, \\ |A2\cap A3\cap A5|=\lfloor 120/30\rfloor =4,|A2\cap A3\cap A7|=\lfloor 120/42\rfloor =2, \\ |A2\cap A5\cap A7|=\lfloor 120/70\rfloor =1,|A3\cap A5\cap A7|=\lfloor 120/105\rfloor =1， \\ |A2\cap A3\cap A5\cap A7|=\lfloor 120/210\rfloor =0, \end{gathered}$$
故 $$\begin{gathered} |\overline{A_2}\cap \overline{A_3}\cap \overline{A_5}\cap \overline{A_7}|=120 \\ –(|A2|+|A3|+|A5|+|A7|) \\ +(|A2\cap A3|+|A2\cap A5|+|A2\cap A7|+|A3\cap A5|+|A3\cap A7|+|A5\cap A7|) \\ –(|A2\cap A3\cap A5|+|A2\cap A3\cap A7|+|A2\cap A5\cap A7|+|A3\cap A5\cap A7|) \\ +|A2\cap A3\cap A5\cap A7|=27 \end{gathered}$$

定理 1.3： S 是一有限集合，P1, P2,…, Pm 是同集合 S 有关的 m 个性质，设$A_i$是 S 中具有性质 Pi 的元素构成的集合(1 ≤ i ≤ m)，则 S 中至少具有一个性质 Pi 的元素的个数为 ∣ A 1 ∪ A 2 ∪ . . . ∪ A m ∣ = ∑ i = 1 m ∣ A i ∣ − ∑ { 1 , 2 , . . m } 的 2 组合 ∣ A i ∩ A j ∣ + ∑ { 1 , 2 , . . m } 的 3 组合 ∣ A i ∩ A j ∩ A k ∣ + . . . + ( − 1 ) m − 1 ∣ A 1 ∩ A 2 ∩ . . . ∩ A m ∣ |A_1\cup A_2\cup...\cup A_m|=\sum_{i=1}^m|A_i|-\sum_{\{1,2,..m\}的2组合} |A_i\cap A_j|+\\\sum_{\{1,2,..m\}的3组合} |A_i\cap A_j \cap A_k|+...+(-1)^{m-1}|A_1\cap A_2 \cap...\cap A_m| ∣A1​∪A2​∪...∪Am​∣=i=1∑m​∣Ai​∣−{1,2,..m}的2组合∑​∣Ai​∩Aj​∣+{1,2,..m}的3组合∑​∣Ai​∩Aj​∩Ak​∣+...+(−1)m−1∣A1​∩A2​∩...∩Am​∣

定理 1.4： 设集合 S 中具有性质集合 P = {P1, P2,…, Pm} 中恰好 r 个性质的元素的个数为 N(r）则$$N(r)=w(r)-\left(\genfrac{}{}{0ex}{}{r+1}{r}\right)w(r+1)+\left(\genfrac{}{}{0ex}{}{r+2}{r}\right)w(r+2)-.+(-1{)}^{m-r}(\genfrac{}{}{0ex}{}{m}{r})w(m)$$其中$w(0)=|S|,w(r)={\sum }_{1\le i_1<...<i_r\le m}N(P_{i_1},P_{i_2},...,P_{i_r})$

2. 容斥原理应用

有限重复数的多重集合的 r 组合数

习题2、 S={3⋅a,4⋅b,5⋅c}的 10 组合数
解: 令 S ∞ = { ∞ ⋅ a , ∞ ⋅ b , ∞ ⋅ c } S_\infty=\{\infty \cdot a,\infty \cdot b,\infty \cdot c\} S∞​={∞⋅a,∞⋅b,∞⋅c},则 S 的 10 组合数为$\left(\genfrac{}{}{0ex}{}{10+3-1}{10}\right)=\left(\genfrac{}{}{0ex}{}{12}{2}\right)=66$
设集合 A 是 $S_{\infty }$的 10 组合全体，则|A| = 66，现在要求在 10 组合中的 a 的个数小于等于 3，b 的个数小于等于 4，c 的个数小于等于 5 的组合数。
定义性质集合 P = {P1, P2, P3}，其中，

• P1：10 组合中 a 的个数大于等于 4；
• P2：10 组合中 b 的个数大于等于 5；
• P3：10 组合中 c 的个数大于等于 6．

将满足性质 Pi 的 10 组合全体记为 Ai (1 ≤ i ≤ 3)．那么，A1 中的元素可以看作是由 $S_{\infty }$的 10 – 4 = 6 组合再拼上 4 个 a 构成的，所以$|A_1|=\left(\genfrac{}{}{0ex}{}{10-4+3-1}{10-4}\right)=28$
类似的有 $|A_2|=\left(\genfrac{}{}{0ex}{}{10-5+3-1}{10-5}\right)=21,|A_3|=\left(\genfrac{}{}{0ex}{}{10-6+3-1}{10-6}\right)=15$
$$\begin{gathered} |A_1\cap A_2|=\left(\genfrac{}{}{0ex}{}{10-5-4+3-1}{10-5-4}\right)=3,|A_1\cap A_3|=\left(\genfrac{}{}{0ex}{}{10-4-6+3-1}{10-4-6}\right)=1,|A_2\cap A_3|=0 \\ |A_1\cap A_2\cap A_3|=0 \end{gathered}$$
而a的个数小于等于3，b的个数小于等于4，c的个数小于等于5的10组合全体为
$|\overline{A_1}\cap \overline{A_2}\cap \overline{A_3}|=|A|-(|A_1|+|A_2|+|A_3|)+(|A1\cap A2|+|A1\cap A3|+|A2\cap A3|)-|A_1\cap A_2\cap A_3|=66-(28+21+15)+(3+1+0)-0=6$

错排问题

集合{1, 2, …, n}的一个错排是该集合的一个满足条件 $i_j\ne j$ 的全排列 $i_1{i}_2\dots i_n$,即集合{1, 2, …, n}的没有一个数字在它的自然顺序位置上的全排列．记为$D_n$
其中 $D_1=0,D_2=1,D_3=2,D_4=9$

定理 2.1：错排递推关系$$\begin{gathered} D_n=(n-1)(D_{n-1}+D_{n-2}) \\ =n{D}_{n-1}+(-1{)}^n \\ =n!(1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+...+(-1{)}^n\frac{1}{n!}) \end{gathered}$$

用 $Q_n$ 表示 {1，2，…，n} 的不出现 12，23，…，(n – 1)n 这些模式的全排列的个数，并规定 $Q_1=1$

定理 2.2：有禁止的排列关系$$Q_n=n!-\left(\genfrac{}{}{0ex}{}{n-1}{1}\right)(n-1)!+(\genfrac{}{}{0ex}{}{n-1}{2})(n-2)!-...+(-1{)}^{n-1}(\genfrac{}{}{0ex}{}{n-1}{n-1})1!$$

3. 鸽巢原理

如果鸽子的数目比巢穴的数目多，那么至少要有一个鸽巢被两只或多只鸽子占据。
如果把 n + 1 个物体放入 n 个盒子，那么至少有一个盒子中有两个或更多的物品。
若把 n (r – 1) + 1 个物体放入 n 个盒子，那么至少有一个盒子中有 r 个物品。

4. Ramsey 定理

任何 6 个人的聚会，其中总会有 3 个人互相认识或 3 个人互相不认识。

定理 4.1：对于任意给定的两个正整数 a 和 b，如果存在最小的正整数 r (a, b)
使得当 N ≥ r (a, b)时，对 $K_N$ 任意进行红、蓝两边着色，$K_N$ 中均有红色 $K_a$，或蓝色 $K_b$则 r (a, b)称为 Ramsey 数

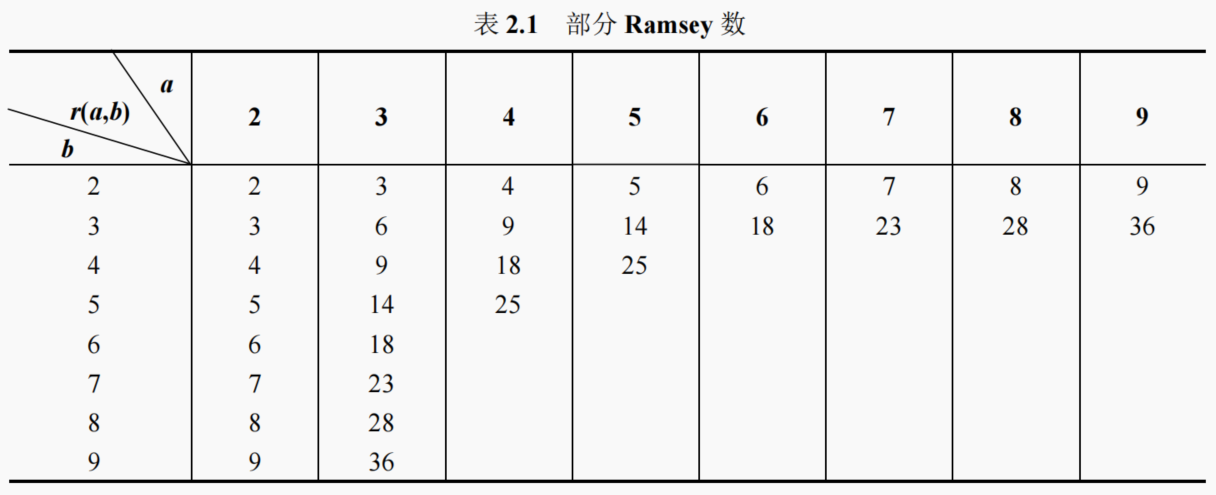
定理 4.2：对任意正整数 a，b，有 r(a, b) = r(b, a)；r(a, 2) = a
对任意正整数 a ≥ 3，b ≥ 3，有 r(a, b) ≤ r(a – 1, b) + r(a, b–1)
对任意正整数 a ≥ 2，b ≥ 2，有 r(a, b) ≤ $\left(\genfrac{}{}{0ex}{}{a+b-2}{a-1}\right)$

作业习题链接：作业 第二章 鸽巢原理

这篇关于【组合数学】容斥鸽巢原理的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---