IMU学习系列（四）---四元数和旋转相关的约定表述

1.四元数的约定表述

1.1 四元数表述的差异

• 根据实部虚部的顺序，左手系和右手系(left-handed,right-handed),操作是旋转向量还是旋转坐标系（active or passive）,操作方向(local to global or global to local),四元数有122中表述方法，其中Hamilton 和JPL是两种常见的表述方式，两者的对比如下表：

• JPL 在航空上经常使用，Hamliton的表述在机器人领域更为常见，和ROS,Eigen,Ceres的程序库中使用的表示一致，和很多应用在IMU上的卡尔曼滤波文献也一致。

1.2 Hamilton vs JPL

• 这里详细比较两者的差异

1.2.1元素的顺序

• Hamilton将实部是第一元素，JPL实部是最后一个元素

1.2.2 左手系和右手系

• 右手系和左手系定义的差别
  
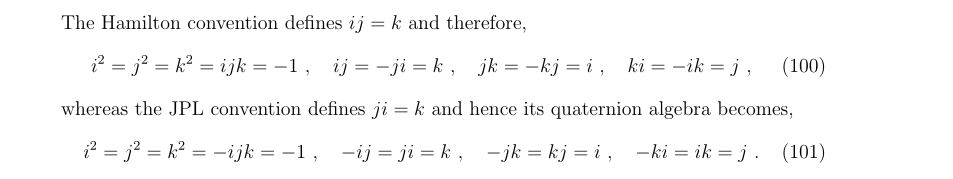
• 两者定义下的四元数是共轭关系
  

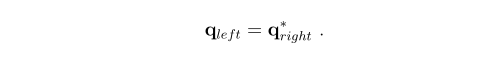
1.2.3 旋转操作的对象

• 一种是假设坐标轴frame不变（active），向量在旋转，这种类似于相机不动，相机里观察的目标在动，或者说整个过程都是假定在一个坐标系下的。

• 一种是假设向量不变(passive),坐标轴在变，类似于相机的视角在变，目标不动，这个和很多SLAM中的表述方式一致，因为SLAM中是假设路标是静止的。如barfoot书中，一个向量r可以由由不同坐标系下的坐标表示，即passive。Hamliton和JPL都是使用的passive的方式。
• passive的表示中，向量r只有一种形式表示，不同时刻的坐标系是在变化的，即向量r在不同时刻有不一样的坐标表示。
  
• active 和passive其实就是相对运动关系：
  

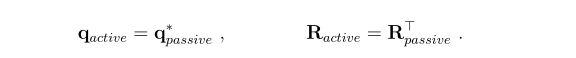
1.2.4 旋转操作的方向

• 我的理解，Local和global是相对的概念，从旋转矩阵的推导我们知道，开始假设机体系b和导航系n是重合的，然后我们推导用空间某个向量r的初始坐标$r_n$和旋转矩阵,表示r在旋转后的b系新的坐标$r_b$.这里b即local，n系即global。
• 或者说我们选择是将相机在新的视角看到的空间某个固定点的坐标转成开始相机视角下的坐标(local-global：$r_n=C_{nb}{r}_b$,barfoot书中的$r_1=C_{12}{r}_2$)；
• 还是旋转将相机在初始视角看到的空间固定点坐标转到相机新的视角下看到的坐标（global-local:$r_b=C_{bn}{r}_n$,barfoot书中$r_2=C_{21}{r}_1$）
• local to global,旋转矩阵下标第一个是旧坐标系，第二个是新坐标系，且下标表述满足链式原则，所以对于添加扰动，local to
  global 是右扰动，global to local是左扰动。后面会证明。
• 两种方式其实也是相对运动的关系
  
• 可以证明，Hamilton和JPL的四元数表示在数值上是相等的。
  

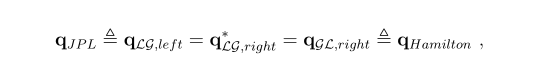
1.3 文章采用的表述

• 文章采用local to global的表示，且简化以下表示：
  

1.4扰动和时间导数

1.4.1右扰动和左扰动

• 局部扰动(local perturbation)是右扰动形式；

local to global的形式下，局部扰动项表示为(下标第一个是旧坐标系G，第二个是新坐标系L)
$$\Delta R_L=\Delta R_{L\tilde{L}}$$
$$\tilde{R}=R_{GL}\Delta R_{L\tilde{L}}$$

• global 扰动是左扰动，证明和局部扰动是相似的：

1.4.2 Hamilton表示下的（L-G）的四元数时间导数

• 所以局部扰动的表达式和一阶泰勒项为:
  
• 四元数时间导数，涉及到四元数运算时，三维角速度向量是用四元数方式表示的，相似的可以推导旋转矩阵的微分,相对于G-L的旋转微分，我们很容易发现L-G的优势，因为实际角速度是机体系b（local）下传感器获得的。
  

1.4.3 其他有用的表述方式

• 通过以上推导而来
  
  1.5 barfoot书中表述
• 根据上述讨论，结合barfoot书中旋转相关公式的形式，可以得知barfoot书中的的表述是：四元数实部在后，使用右手系，passive方式，采用左扰动/全局扰动（global
  to local）。

2.旋转角速率表示旋转积分

• 这里不采用文章中的推导，从笔记(2)中，四元数和旋转向量出发推导：
  $$q_{n+1}=q_n\otimes e^u=q_n\otimes e^{\omega \Delta t/2}$$
  泰勒展开得到：
  

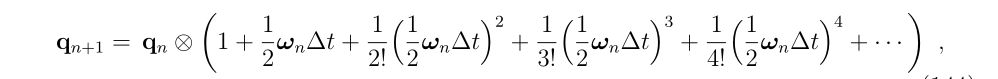
2.1零阶积分

• 零阶积分是假设$\dot{\omega }=0$,这里零阶积分方法的不同主要在于参数$\omega$值的选取时间的不同。去$({\omega }_n,{\omega }_{n+1})$的均值，有类似平滑的作用，是okvis采用的方法。
  

2.2一阶积分

一阶积分是假设$\omega$的二阶微分为0，一微分是常数，利用插值方法得到:

• 代入2.1中的泰勒展开式，并利用叉乘性质简化：
  

2.3归一化处理

• 由于积分舍去了高阶项，使得积分后的四元数不再是单位四元数，需要从新归一化