scikit-opt几种数值模拟退火的代码示例，和参数详解,以及基础模拟退火的原理代码示例

本文主要是介绍scikit-opt几种数值模拟退火的代码示例，和参数详解,以及基础模拟退火的原理代码示例，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

python基础模拟退火原理示例

模拟退火的特性决定了一般可以用于算法的调参，相比较遗传算法来说，普遍更快一些，但是也更容易陷入局部最优。相对来说，遗传算法的更新解机制是在最每一个局部最优解附近盘旋游荡，则更容易达到全局最优，但是计算量则更大。

# -*- encoding: utf-8 -*-
'''
@File    :   simulate_anneal.py
@Time    :   2020/10/28 12:45:28
@Author  :   DataMagician 
@Version :   1.0
@Contact :   408903228@qq.com
'''# here put the import libimport numpy as np
import matplotlib.pyplot as plt# ### $ 根据热力学的原理，在温度为T时，出现能量差为dE的降温的概率为P(dE)，表示为：$
# # $ P(dE) = exp( dE/(k*T) ) $
# ### $ 其中k是一个常数，exp表示自然指数，且dE<0(温度总是降低的)。这条公式指明了 $# # 单变量退火
def PDE(DE, T, k=1):'''Args:DE:t:k:Returns:'''return np.exp((DE) / (k * T))def DE_function(new, old):'''Args:new:old:Returns:'''return new - olddef jump(DE, T, k=1):'''Args:DE:T:k:Returns:'''return PDE(DE, T, k) > np.random.rand() and 0 or 1def simulate_anneal(func,parameter={"T": 1, #系统的温度，系统初始应该要处于一个高温的状态 初始温度越高，且马尔科夫链越长，算法搜索越充分，得到全局最优解的可能性越大，但这也意味着需要耗费更多的计算时间"T_min": 0, #温度的下限，若温度T达到T_min，则停止搜索"r": 0.0001, #用于控制降温的快慢 值越小T更新越快，退出越快"expr": 0, #初始解"jump_max": np.inf,#最大回炉停留次数"k":1 # k越小越不容易退出}):'''Args:func:parameter:Returns:'''path, funcpath = [], []T = parameter["T"]  # 系统温度，初时应在高温T_min = parameter["T_min"]  # 最小温度值r = parameter["r"]  # 降温速率counter = 0expr = parameter["expr"]  # 假设初解jump_max = parameter["jump_max"]  # 最大冷却值jump_counter = 0k = parameter["k"]while T > T_min:counter += 1new_expr = func.__next__()  # 迭代新解funcpath.append(new_expr)DE = DE_function(new_expr , expr)if DE <= 0:# 如果新解比假设初解或者上一个达标解要小，就更新解expr = new_expr# 跳出域值更新为0 jump_counter = 0elif DE > 0:# 如果新解比假设初解或者上一个达标解要大，就不更新解expr = exprif jump(DE, T,k):# 每更新一次T更新一次T *= rjump_counter += 1if jump_counter > jump_max:print("最大回炉冷却次数:", jump_counter)return expr, path, funcpathpath.append(expr)print("{}{}{}{}{}{}{}{}".format('系统温度:', T, ' 新状态:', expr, ' 迭代轮次:',counter, ' DE:', DE))return expr, path, funcpathif __name__ == "__main__":def f():  # 待优化最小函数'''Returns:'''for x in np.random.randn(1000):yield xexpr, path, funcpath = simulate_anneal(f(),parameter={"T": 1,"T_min": 0,"r": 0.4,"expr": 0,"jump_max": 1000,"k":0.000001})print(expr)plt.figure(figsize=(16, 9))  # %%plt.plot(path, c='g')plt.plot(funcpath, c='r')plt.show()plt.close()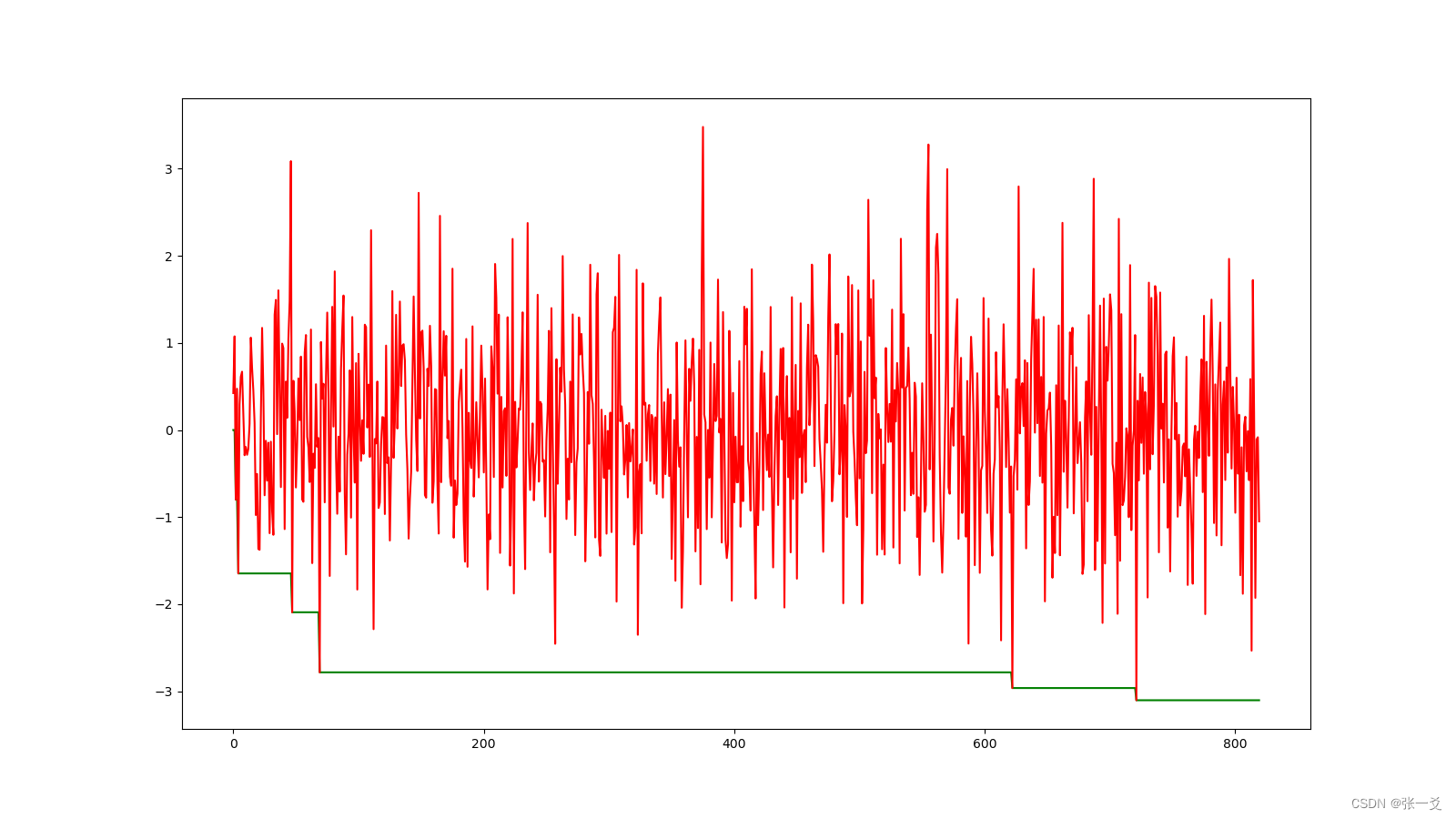

请添加图片描述

快速模拟退火

from sko.SA import SAFast
import matplotlib.pyplot as plt
import pandas as pddef demo_func(x):return x[0] ** 2 + (x[1] - 0.05) ** 2 + x[2] ** 2sa = SAFast(func=demo_func, x0=[1, 1, 1] # 初始x解，初始解越大则越难到达最小值,越小则越容易错过, T_max=1 #系统的温度，系统初始应该要处于一个高温的状态 初始温度越高，且马尔科夫链越长，算法搜索越充分，得到全局最优解的可能性越大，但这也意味着需要耗费更多的计算时间, T_min=1e-9  #温度的下限，若温度T达到T_min，则停止搜索, L=300 #最大迭代次数,每个温度下的迭代次数（又称链长）, max_stay_counter=100 # 最大冷却停留计数器，保证快速退出,如果 best_y 在最大停留计数器次数（也称冷却时间）内保持不变，则停止运行,lb = [-1,1,-1] #x的下限,ub = [2,3,4] #x的上限#,hop = [3,2,1] # x 的上下限最大差值 hop=ub-lb ,m = 1 # 0-正无穷，越大，越容易冷却退出,n = 1 # # 0-正无穷，越大，越不容易冷却退出,quench = 1 # 淬火指数，0-正无穷，越小则越慢，但是越能求出最小，越大则越快，但是容易陷入局部最优)
best_x, best_y = sa.run()
print('best_x:', best_x, 'best_y:', best_y,"y_history:",len(sa.best_y_history),sa.iter_cycle)
plt.plot(pd.DataFrame(sa.best_y_history).cummin(axis=0))
plt.show()

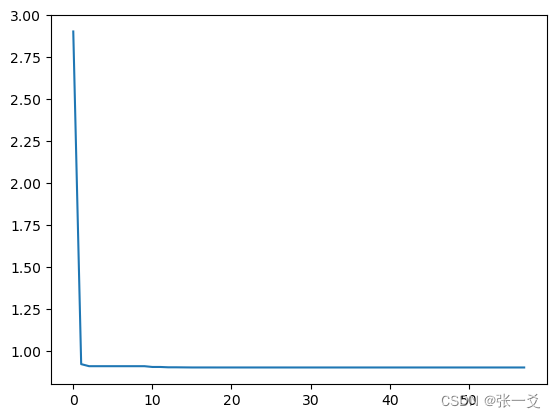
请添加图片描述

纯数值模拟退火

from sko.SA import SimulatedAnnealingValue
import matplotlib.pyplot as plt
import pandas as pddef demo_func(x):return x[0] ** 2 + (x[1] - 0.05) ** 2 + x[2] ** 2sa = SimulatedAnnealingValue(func=demo_func, x0=[1, 1, 1] # 初始x解，初始解越大则越难到达最小值,越小则越容易错过, T_max=1 #系统的温度，系统初始应该要处于一个高温的状态 初始温度越高，且马尔科夫链越长，算法搜索越充分，得到全局最优解的可能性越大，但这也意味着需要耗费更多的计算时间, T_min=1e-9  #温度的下限，若温度T达到T_min，则停止搜索, L=300 #最大迭代次数,每个温度下的迭代次数（又称链长）, max_stay_counter=100000 # 冷却停留计数器,如果 best_y 在最大停留计数器次数（也称冷却时间）内保持不变，则停止运行,lb = [-1,1,-1] #x的下限,ub = [2,3,4] #x的上限#,hop = [3,2,1] # x 的上下限最大差值 hop=ub-lb ,learn_rate = 0.0001 # 学习率，用于控制降温的快慢 值越小T更新越快，退出越快)
best_x, best_y = sa.run()
print('best_x:', best_x, 'best_y:', best_y,"y_history:",len(sa.best_y_history))
plt.plot(pd.DataFrame(sa.best_y_history).cummin(axis=0))
plt.show()

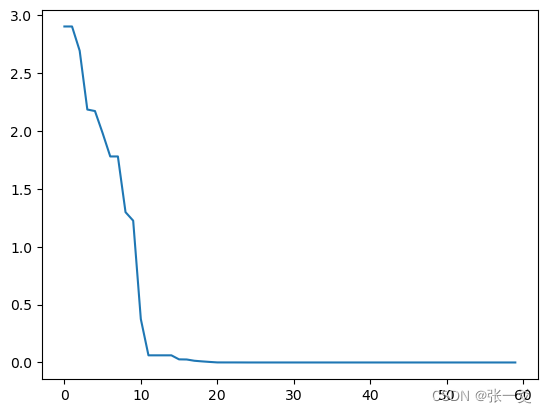
请添加图片描述

柯西模拟退火

from sko.SA import SACauchy
import matplotlib.pyplot as plt
import pandas as pddef demo_func(x):return x[0] ** 2 + (x[1] - 0.05) ** 2 + x[2] ** 2sa = SACauchy(func=demo_func, x0=[1, 1, 1] # 初始x解，初始解越大则越难到达最小值,越小则越容易错过, T_max=1 #系统的温度，系统初始应该要处于一个高温的状态 初始温度越高，且马尔科夫链越长，算法搜索越充分，得到全局最优解的可能性越大，但这也意味着需要耗费更多的计算时间, T_min=1e-9  #温度的下限，若温度T达到T_min，则停止搜索, L=300 #最大迭代次数,每个温度下的迭代次数（又称链长）, max_stay_counter=100 # 冷却停留计数器,如果 best_y 在最大停留计数器次数（也称冷却时间）内保持不变，则停止运行,lb = [-1,1,-1] #x的下限,ub = [2,3,4] #x的上限#,hop = [3,2,1] # x 的上下限最大差值 hop=ub-lb ,learn_rate = 0.1 # 学习率，用于控制降温的快慢 值越大T更新越快，退出越快)
best_x, best_y = sa.run()
print('best_x:', best_x, 'best_y:', best_y,"y_history:",len(sa.best_y_history))
plt.plot(pd.DataFrame(sa.best_y_history).cummin(axis=0))
plt.show()

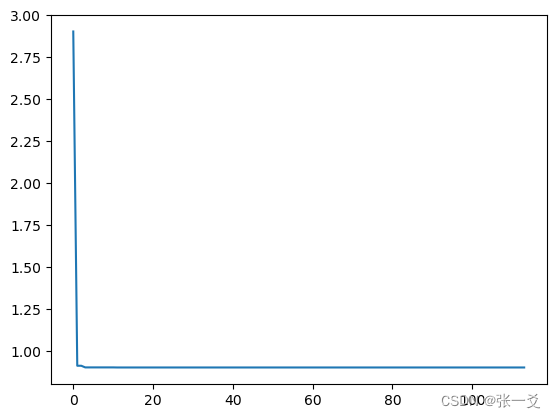
请添加图片描述

玻尔兹曼模拟退火

from sko.SA import SABoltzmann
import matplotlib.pyplot as plt
import pandas as pddef demo_func(x):return x[0] ** 2 + (x[1] - 0.05) ** 2 + x[2] ** 2sa = SABoltzmann(func=demo_func, x0=[1, 1, 1] # 初始x解，初始解越大则越难到达最小值,越小则越容易错过, T_max=1 #系统的温度，系统初始应该要处于一个高温的状态 初始温度越高，且马尔科夫链越长，算法搜索越充分，得到全局最优解的可能性越大，但这也意味着需要耗费更多的计算时间, T_min=1e-9  #温度的下限，若温度T达到T_min，则停止搜索, L=300 #最大迭代次数,每个温度下的迭代次数（又称链长）, max_stay_counter=100 # 冷却停留计数器,如果 best_y 在最大停留计数器次数（也称冷却时间）内保持不变，则停止运行# ,lb = [-1,1,-1] #x的下限# ,ub = [2,3,4] #x的上限,hop = [3,2,1] # x 的上下限最大差值 hop=ub-lb ,learn_rate = 0.1 # 学习率，用于控制降温的快慢 值越大T更新越快，退出越快)
best_x, best_y = sa.run()
print('best_x:', best_x, 'best_y:', best_y,"y_history:",len(sa.best_y_history))
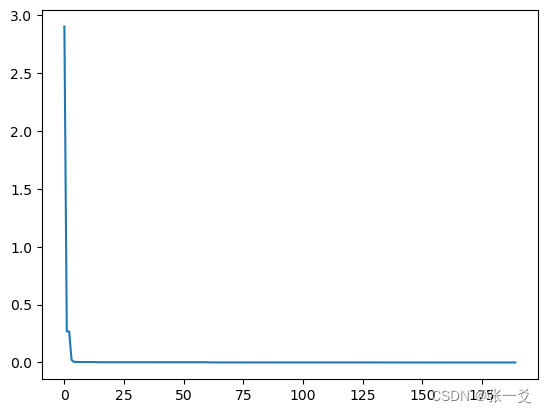
plt.plot(pd.DataFrame(sa.best_y_history).cummin(axis=0))
plt.show()