本文主要是介绍线性系统理论 -- 降阶观测器的设计，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
定理： 若系统能观测，且rankC=m，则系统的状态观测器的最小维数是(n-m)。
线性定常时不变系统方程如下（以三阶(n=3)单入单出系统为例，有m=rankC=1）：
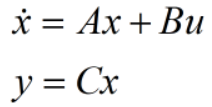
取变换阵P，有：
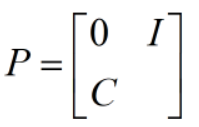
对上述系统方程进行线性变换，
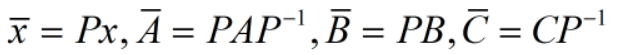
得到如下形式：
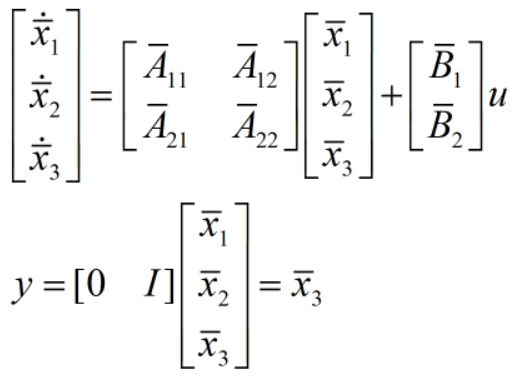
输出y直接给出
。于是状态估计时，只需对 n-m=2 维的
、
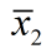进行估计即可。这就是说，降阶观测器的维数为n-m=2。
降阶观测器方程为：
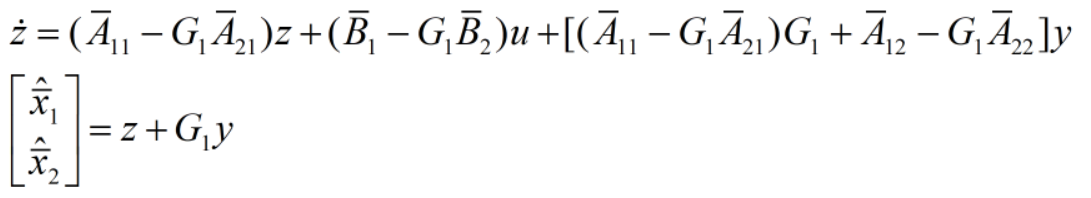
只需要选择合适的G1阵，使得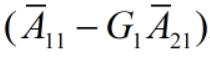 
所有的特征值具有期望的特征值即可。
举例如下：
给定连续线性时不变系统：
试确定特征值为-3，-4的二维状态观测器。
解答：
先判断系统是否能观测：
故系统能观测。
选取变换阵P：
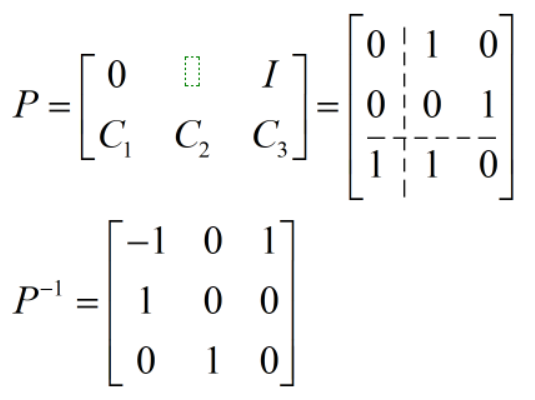
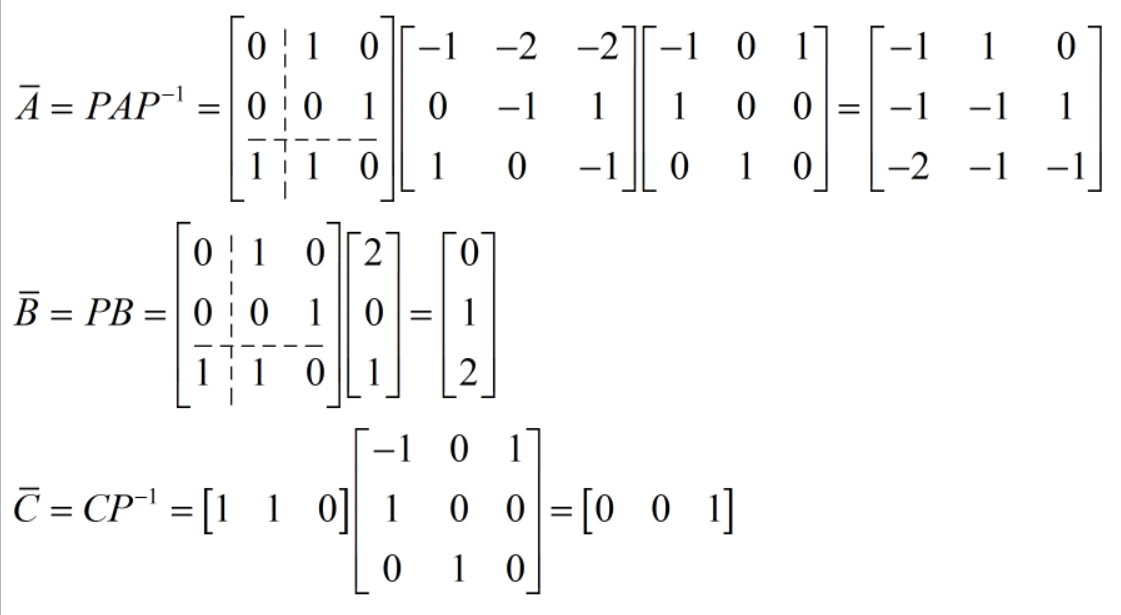可见状态变量
可由y直接提供。现只需要设计一个二阶状态观测器来估计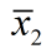即可。
设G1阵为：
则有：
期望的特征多项式为：
对照系数得：
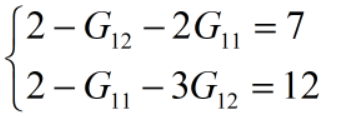
得到：
从而：
系统的二阶降维观测器为：
其中：
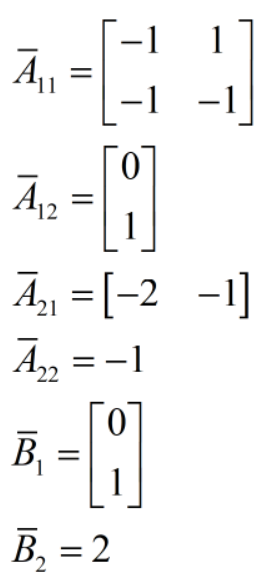
这篇关于线性系统理论 -- 降阶观测器的设计的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
