离散数学-集合论基础

本文主要是介绍离散数学-集合论基础，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

3.1集合的基本概念
1）集合及元素

2）集合的表示

3）集合的关系

4）特殊集合

3.2集合的运算

并、交、差、对称差

3.3集合的划分与覆盖

3.4排斥包含管理

3.1集合的基本概念

1）集合及元素

将某种具有同种属性的个体组成的整体，称为集合。

集合通常用大写英文字母表示，用小写英文字母表示集合的元素。

若个体a属于集合A，则称a属于A，记作aA；否则，a不属于A，记作aA。

若A集合的元素的个数是有限的，则称其为有限集合。

元素的个数称为集合A的基，记作|A|；否则，称为无限集合。

含有n个元素的集合称为n元集。

（1）集合可以由热议类型的元素组成，可以是具体的也可以是抽象的，一个集合的元素可以是另一个集合的元素，但是不允许以集合自身为元素。

（2）元素与集合是一种隶属关系。任何一个个体对一个集合来说，要么属于该集合，要么不属于

（3）集合的元素必须：确定的、可区分的、不重复、无序。

常用的集合有自然数集N，整数集Z、有理数集Q、实数集R、素数集P等。

2）集合的表示

表示集合的方式常用的有三种：列举法、描述法、画图法

列举法：以任意顺序、不重复写出集合所有的元素，中间用逗号隔开，两边用花括号{}括起来。

例如：A={1，2，3，4，5}

有时，如果集合的元素有一定规律，可以用部分列举法表示

例如：A为全体小写字母：A = {a,b,c...x,y,z}

           A为1到无穷大的整数：A= {1，2，3，... }

描述法：描述法也称谓词表示法，即用谓词描述集合元素的共同熟悉（就是谓词逻辑的应用）。

例如：设谓词P(x)表示集合元素x具有属性P，具有属性P的所有个体组成的集合A，记作A={x|P(x)}

画图法：利用平面图形表示集合，以英国数学家（John Ven）的名字命名，直观形象便于理解。

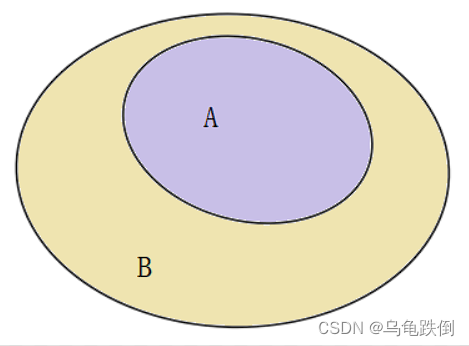
3）集合的关系

（1）设A、B是集合，如果集合A的每个元素都是B的元素，则称A是B的子集，或者A包含于B，或者B包含A，记作AB。

如果A有任何一个元素不属于B，那么A不是B的子集。

4）特殊集合

以任意顺序、不重复写出集合所有的元素，中间用逗号隔开，两边用花括号{}括起来。

（1）空集：不含任何元素的集合叫做空集，记作Ø

（2）空集是任何集合的子集。

（注意：Ø和{Ø}是两个不同的集合）

 （3）任何一个集合都有至少两个子集，一个是其本身，一个是空集Ø。

（4）空集Ø只有一个子集，就是其本身。

（5）全集：在问题讨论的范围内，如果所有的集合都是某个集合E的子集，则称该集合E为全集

（6）幂集：以集合A的所有子集为元素的集合称为A的幂集。（也就是说，幂集的元素的集合）

3.2集合的运算

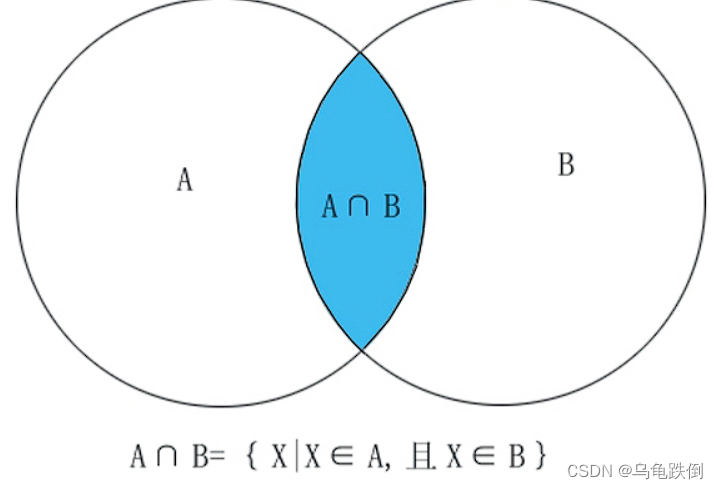
1）交运算

设A、B为集合，由A和B上的所共有的元素组成的集合，称为A与B的交集，记作A∩B

即A∩B = {x|xA∧xB}

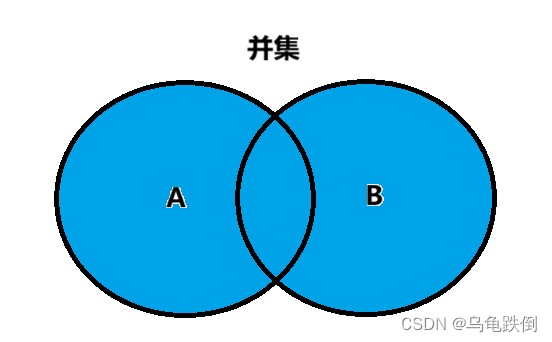
2）并运算

设A、B为集合，由A和B的所有元素组成的集合，称为A和B的并集，记作A∪B

即A∪B = {x|xA∨xB}

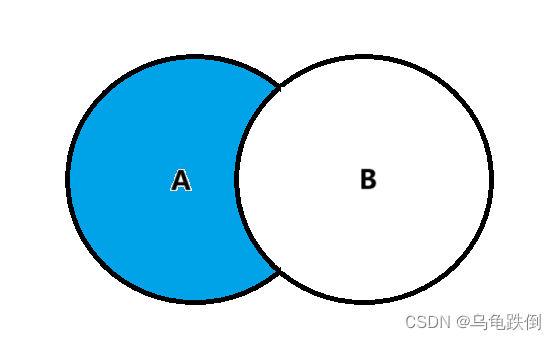
3）差运算

设A、B为集合，由属于A但不属于B的所有元素组成的集合，称为B对于A的补集或相对补，或者A减B的差集，记作A-B

即A-B = {x|xA ∧ xB}

4）对称差运算

设A、B为集合，由属于A或者属于B的，但是不同时属于A与B的元素组成的集合，称为A与B的对称差，记作A⊕B

即A⊕B ={ x| {x|xA ∧ xB}  ∨  {x|xA ∧ xB}  }

总结起来就是：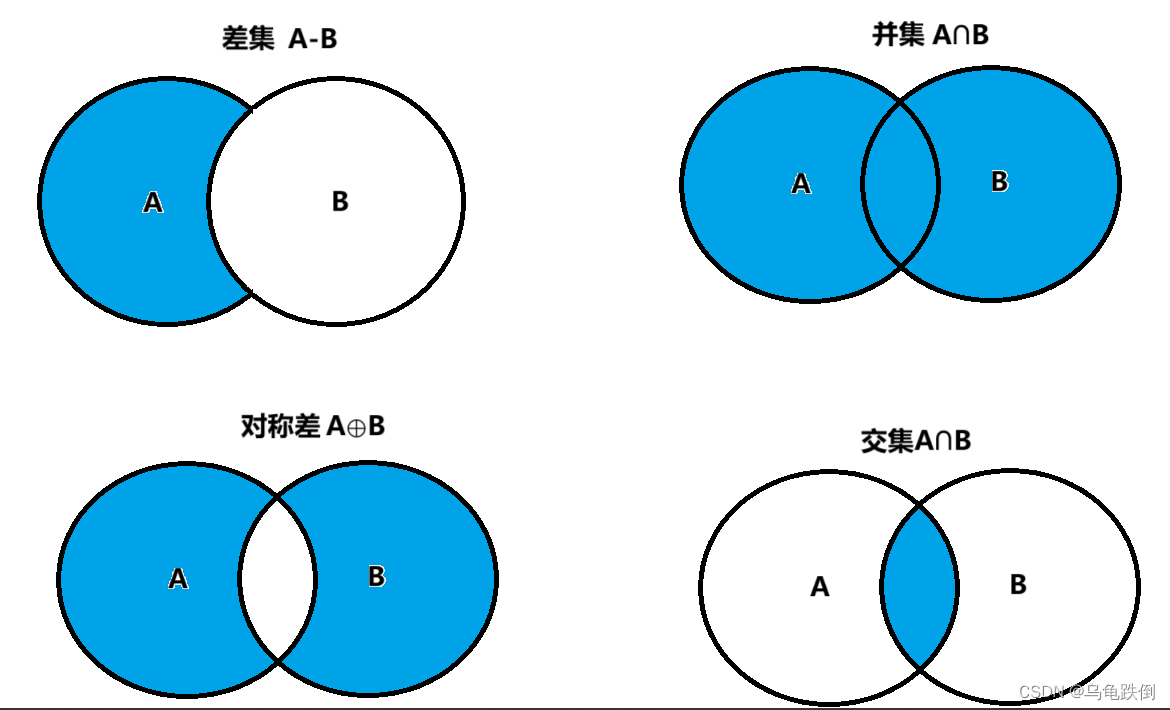

5)集合运算的性质

设A、B、C为集合。比较有用的：

1）幂等律    A⋂A =A         A⋃A = A

2）零律   A⋂Ø =Ø         A⋃E = E     A⊕Ø=Ø

4）交换律  A⋂B =A⋂B  A⋃B = B⋃A 

5）结合律  A⋂(B⋂C) =(A⋂B)⋂C    A⋃(B⋃C) = (A⋃B)⋃C 

3.3集合的划分与覆盖

划分：即将集合划分为几个块，这一块可以是一个元素的集合，也可以是多个元素的集合。

覆盖：在A集合中，B中全都有，则称B为A的覆盖。（简单理解就是盖住了，大于等于的关系）

注意：

1）划分必是覆盖，覆盖不一定是划分

2）集合的覆盖与划分是不唯一的

3）集合A的每个元素至少属于A的覆盖中的子集，属于且仅属于A的划分中的一个划分块。

下面是课本的例题，一看就懂：

3.4包含排斥原理

设、为有限集合，，则  | ⋃ | = | | +|| -|⋂|

这篇关于离散数学-集合论基础的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---