本文主要是介绍【Redis核心原理和应用实践】应用 7:一毛不拔 —— 漏斗限流,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
漏斗限流是最常用的限流方法之一,顾名思义,这个算法的灵感源于漏斗(funnel)的结构。

漏斗的容量是有限的,如果将漏嘴堵住,然后一直往里面灌水,它就会变满,直至再也装不进去。如果将漏嘴放开,水就会往下流,流走一部分之后,就又可以继续往里面灌水。
如果漏嘴流水的速率大于灌水的速率,那么漏斗永远都装不满。如果漏嘴流水速率小于灌水的速率,那么一旦漏斗满了,灌水就需要暂停并等待漏斗腾空。
所以,漏斗的剩余空间就代表着当前行为可以持续进行的数量,漏嘴的流水速率代表着系统允许该行为的最大频率。下面我们使用代码来描述单机漏斗算法。
# coding: utf8 import time class Funnel(object): def __init__(self, capacity, leaking_rate): self.capacity = capacity # 漏斗容量 self.leaking_rate = leaking_rate # 漏嘴流水速率 self.left_quota = capacity # 漏斗剩余空间 self.leaking_ts = time.time() # 上一次漏水时间 def make_space(self): now_ts = time.time() delta_ts = now_ts - self.leaking_ts # 距离上一次漏水过去了多久 delta_quota = delta_ts * self.leaking_rate # 又可以腾出不少空间了 if delta_quota < 1: # 腾的空间太少,那就等下次吧 return self.left_quota += delta_quota # 增加剩余空间 self.leaking_ts = now_ts # 记录漏水时间 if self.left_quota > self.capacity: # 剩余空间不得高于容量 self.left_quota = self.capacity def watering(self, quota): self.make_space() if self.left_quota >= quota: # 判断剩余空间是否足够 self.left_quota -= quota return True return False funnels = {} # 所有的漏斗 # capacity 漏斗容量
# leaking_rate 漏嘴流水速率 quota/s
def is_action_allowed( user_id, action_key, capacity, leaking_rate): key = '%s:%s' % (user_id, action_key) funnel = funnels.get(key) if not funnel: funnel = Funnel(capacity, leaking_rate) funnels[key] = funnel return funnel.watering(1) for i in range(20): print is_action_allowed('laoqian', 'reply', 15, 0.5) 再提供一个 Java 版本的:
public class FunnelRateLimiter { static class Funnel { int capacity; float leakingRate; int leftQuota; long leakingTs; public Funnel(int capacity, float leakingRate) { this.capacity = capacity; this.leakingRate = leakingRate; this.leftQuota = capacity; this.leakingTs = System.currentTimeMillis(); } void makeSpace() { long nowTs = System.currentTimeMillis(); long deltaTs = nowTs - leakingTs; int deltaQuota = (int) (deltaTs * leakingRate); if (deltaQuota < 0) { // 间隔时间太长,整数数字过大溢出 this.leftQuota = capacity; this.leakingTs = nowTs; return; } if (deltaQuota < 1) { // 腾出空间太小,最小单位是 1 return; } this.leftQuota += deltaQuota; this.leakingTs = nowTs; if (this.leftQuota > this.capacity) { this.leftQuota = this.capacity; } } boolean watering(int quota) { makeSpace(); if (this.leftQuota >= quota) { this.leftQuota -= quota; return true; } return false; } } private Map<String, Funnel> funnels = new HashMap<>(); public boolean isActionAllowed(String userId, String actionKey, int capacity, float leakingRate) { String key = String.format("%s:%s", userId, actionKey); Funnel funnel = funnels.get(key); if (funnel == null) { funnel = new Funnel(capacity, leakingRate); funnels.put(key, funnel); } return funnel.watering(1); // 需要 1 个 quota }
} Funnel 对象的 make_space 方法是漏斗算法的核心,其在每次灌水前都会被调用以触发漏水,给漏斗腾出空间来。能腾出多少空间取决于过去了多久以及流水的速率。Funnel 对象占据的空间大小不再和行为的频率成正比,它的空间占用是一个常量。
问题来了,分布式的漏斗算法该如何实现?能不能使用 Redis 的基础数据结构来搞定?
我们观察 Funnel 对象的几个字段,我们发现可以将 Funnel 对象的内容按字段存储到一个 hash 结构中,灌水的时候将 hash 结构的字段取出来进行逻辑运算后,再将新值回填到 hash 结构中就完成了一次行为频度的检测。
但是有个问题,我们无法保证整个过程的原子性。从 hash 结构中取值,然后在内存里运算,再回填到 hash 结构,这三个过程无法原子化,意味着需要进行适当的加锁控制。而一旦加锁,就意味着会有加锁失败,加锁失败就需要选择重试或者放弃。
如果重试的话,就会导致性能下降。如果放弃的话,就会影响用户体验。同时,代码的复杂度也跟着升高很多。这真是个艰难的选择,我们该如何解决这个问题呢?Redis-Cell 救星来了!
Redis-Cell
Redis 4.0 提供了一个限流 Redis 模块,它叫 redis-cell。该模块也使用了漏斗算法,并提供了原子的限流指令。有了这个模块,限流问题就非常简单了。
该模块只有 1 条指令 cl.throttle,它的参数和返回值都略显复杂,接下来让我们来看看这个指令具体该如何使用。
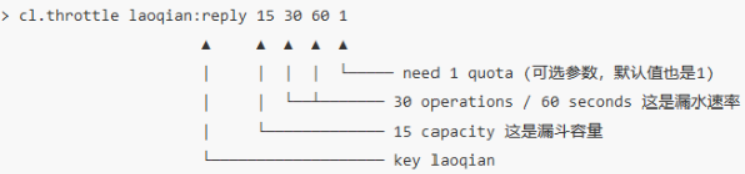
上面这个指令的意思是允许「用户老钱回复行为」的频率为每 60s 最多 30 次(漏水速率),漏斗的初始容量为 15,也就是说一开始可以连续回复 15 个帖子,然后才开始受漏水速率的影响。我们看到这个指令中漏水速率变成了 2 个参数,替代了之前的单个浮点数。用两个参数相除的结果来表达漏水速率相对单个浮点数要更加直观一些。
> cl.throttle laoqian:reply 15 30 60
1) (integer) 0 # 0 表示允许,1 表示拒绝
2) (integer) 15 # 漏斗容量 capacity
3) (integer) 14 # 漏斗剩余空间 left_quota
4) (integer) -1 # 如果拒绝了,需要多长时间后再试(漏斗有空间了,单位秒)
5) (integer) 2 # 多长时间后,漏斗完全空出来(left_quota==capacity,单位秒) 在执行限流指令时,如果被拒绝了,就需要丢弃或重试。cl.throttle 指令考虑的非常周到,连重试时间都帮你算好了,直接取返回结果数组的第四个值进行 sleep 即可,如果不想阻塞线程,也可以异步定时任务来重试。
思考
漏斗限流模块除了应用于 UGC,还能应用于哪些地方?
拓展阅读
《Redis-Cell 作者 Itamar Haber 其人趣事》
Redis-Cell 作者 Itamar Haber 的介绍很有意思——一个「自封」的 Redis 极客。还有,Cell 这个模块居然是用 Rust 编写的。—— 原来 Redis 模块可以使用 Rust 编写?!
这意味着我们不用去搞古老的 C 语言了。老钱表示要重新拾起放弃很久的 Rust 语言。
哎,干程序员这一行,真是要活到老,学到死啊!
这篇关于【Redis核心原理和应用实践】应用 7:一毛不拔 —— 漏斗限流的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!


