本文主要是介绍CSP:重庆八中宏帆初级中学校新初二编程社C2024liuyanjia暑假一期集训总结(2/6)),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一、引言(废话)
近年来,计算机科学成为学科的一大热门,对经济社会发展起到十分巨大的推进作用。信息学竞赛成为五大学科竞赛之一,国家出台许多重要的政策,激起大中小学学生对计算机科学的热爱。但是许多计算机科学爱好者对图论的理论不够系统、算法理解不当、细节掌握不熟、常用技巧不会的问题。而许多培训机构及直播课对此解析不够清晰、完整,本文将探究图论的基础理论与算法原理,并以此为视角,总结经验,发表个人看法,查找图论的实际操作中的现存问题,略析其原因,并且给出相应的解决方法,以供参考。
关键词:图论;并查集;树状数组;最小生成树;最短路;hash;离散化。
二、图论——概念,表示与遍历
1.复习——树的存储
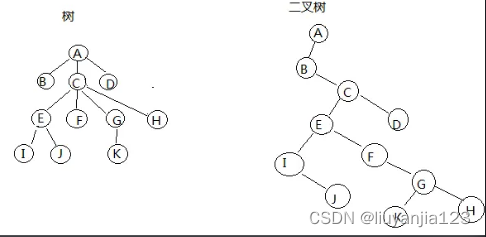
(一)分析
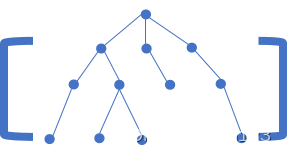
就例如这样的,便是一棵树。(左边是一个普通哥,右边是一个二叉哥)。
既然是一棵树,那么就会有爸爸和儿子。特别地,二叉树有左儿子、右儿子。
那么、我们只需要知道一棵树的爸爸和儿子是谁,我们就可以知道这棵树长什么样子了。
那么,我们来看看这道题目吧!
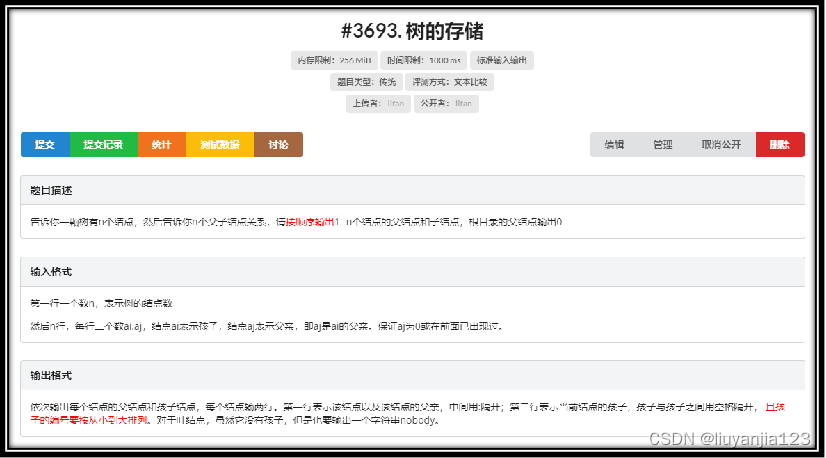
(二)、CODE:
#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int n, b[N];
struct Node {int fa, len, c[6];
}a[N];
void inser(int xx, int yy) {a[xx].fa = yy;a[yy].c[++a[yy].len] = xx;
}
void build() {cin >> n;for (int i = 1;i <= n;i++) {int x, y;scanf("%d%d", &x, &y);inser(x, y);}
}
int main() {build();for (int i = 1;i <= n;i++) {printf("%d:%d\n", i, a[i].fa);if (!a[i].len) {puts("nobody");continue;}sort(a[i].c + 1, a[i].c + a[i].len + 1);for (int j = 1;j <= a[i].len;j++) {printf("%d ", a[i].c[j]);}puts("");}return 0;
}
2.引入
(一)、数据结构的四种形态
F i r s t First First 集合
S e c o n d Second Second 链表、队列、栈
T h i r d Third Third 树
F o u r t h Fourth Fourth 图

F i f t h Fifth Fifth 总结
集合:无序、查询方便;但可支持随机访问,效率低下
链表:有序、在特殊情况下十分方便有用,但不支持随机访问。
树:特殊,支持随机访问、查询效率高、但有点难写。
图:等着你来探索。
(二)、图的概念
One 图的图片
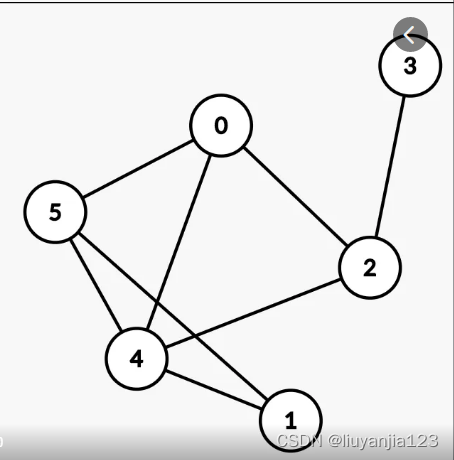
不带权图
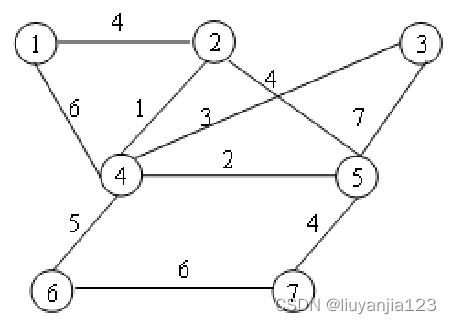
带权图
Two 图的术语
无向图术语
两个顶点之间如果有边连接,那么就视为两个顶点相邻。
路径:相邻顶点的序列。
圈:起点和终点重合的路径。
连通图:任意两点之间都有路径连接的图。
度:顶点连接的边数叫做这个顶点的度。
树:没有环的连通图。
森林:没有环的非连通图。
有向图术语
特点 :在有向图中,边是单向的:每条边所连接的两个顶点是一个有序对,他们的邻接性是单向的。
有向环:一条至少含有一条边且起点和终点相同的有向路径。
有向无环图:在图论中,如果一个有向图无法从某个顶点出发经过若干条边回到该点,则这个图是一个有向无环图(DAG图)。
度:一个顶点的入度与出度之和称为该顶点的度。
1)入度:以顶点为弧头的边的数目称为该顶点的入度。
2)出度:以顶点为弧尾的边的数目称为该顶点的出度。
简化一下:
入度 = 有多少条边可以到这个点。
出度 = 这个点可以直接到达其他点的个数。
3.图的储存与表示
(一)、邻接矩阵
O n e One One 概念
用一个二维数组存放顶点间关系(边或弧)的数据,这个二维数组称为邻接矩阵。邻接矩阵又分为有向图邻接矩阵和无向图邻接矩阵。
T w o Two Two 例子
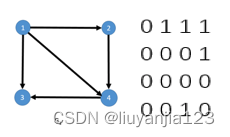
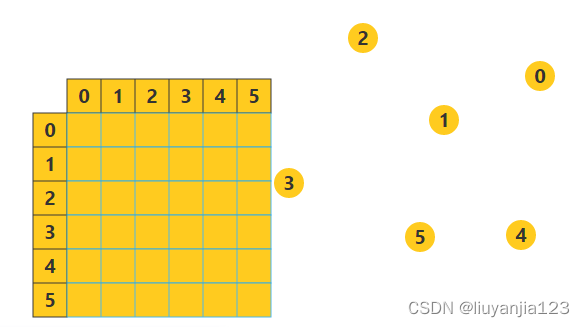
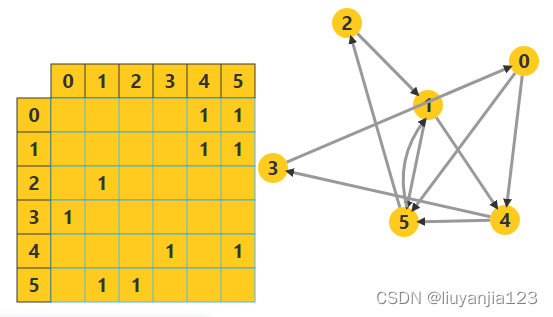
T h r e e Three Three 使用
初始化
初始化的过程很简单,只需要把数组初始化为 0 0 0 即可。可以借助 m e m s e t memset memset来快速地将一个数组中的所有元素都初始化为 0 0 0。
memset(G, 0, sizeof(G));
也可以直接用循环初始化。
for (int i = 1; i <= n; i++) // n 为数组第一维大小for (int j = 1; j <= m; j++) // m 为数组第二维大小G[i][j] = 0;
提示:一般来讲,我们用 G G G这个名称来作为图的数组名。
插入边
G[u][v] = 1;
G[v][u] = 1;
访问边
如果 G [ u ] [ v ] = 1 G[u][v] = 1 G[u][v]=1,说明有一条从 u u u 到 v v v 的边,否则没有从 u u u 到 v v v 的边。
特殊的,带权图只需将上文的 1 1 1改成权值即可。
同时,在存储带权图时,要注意重边的处理。
可将:
G[u][v] = G[v][u] = w;
改成:
G[u][v] = G[v][u] = max(G[u][v], w);
即可处理重边。
Four 优缺点
1.优点:在表示稠密图时节省空间。
2.缺点:在表示稀疏图时浪费空间和时间。
(二)、邻接表
O n e One One 优缺点
1.优点
节省空间:当图的顶点数很多、但是边的数量很少时,如果用邻接矩阵,我们就需要开一个很大的二维数组,最后我们需要存储 n 2 n^2 n2个数剧。但是用邻接表,最后我们存储的数据量只是边数 m m m的两倍。
2.缺点
随机访问效率低。比如,我们需要询问点 a a a 是否和点 b b b 相连,我们就要遍历 G [ a ] G[a] G[a] ,检查这个 v e c t o r vector vector 里是否有 b b b。而在邻接矩阵中,只需要根据 G [ a ] [ b ] G[a][b] G[a][b] 就能判断。
T w o Two Two 思想
对于图中的每一个顶点,用一个数组来记录这个点和哪些点相连。由于相邻的点会动态的添加,所以对于每个点,我们需要用 v e c t o r vector vector来记录。
T h r e e Three Three 使用
利用 v e c t o r vector vector 中的 p u s h push push_ b a c k back back 操作.
G[u].push_back(v);
G[v].push_back(u);
F o u r Four Four 图示
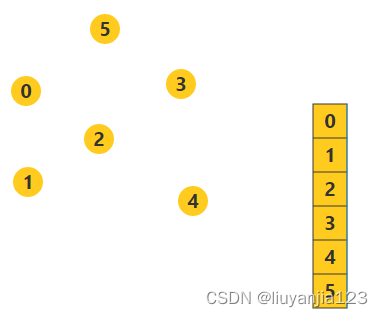
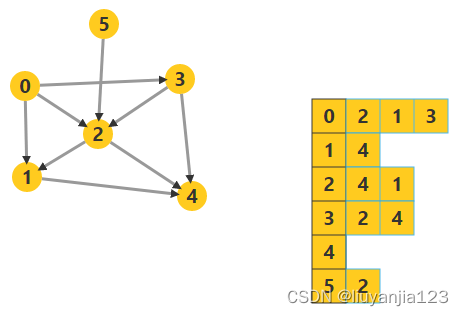
(三)、代码
F i r s t First First 邻接矩阵
#include <bits/sstdc++.h>
using namespace std;
const int N = 1e3 + 5;
int n, m, G[N][N];
int main() {cin >> n >> m;for (int i = 1, u, v; i <= m; i++) {cin >> u >> v;G[u][v] = G[v][u] = 1;}for (int i = 1;i <= n;i++) {for (int j = 1;j <= n;j++) {cout << G这篇关于CSP:重庆八中宏帆初级中学校新初二编程社C2024liuyanjia暑假一期集训总结(2/6))的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







