只需一招 彻底攻克c语言指针,【A-level高数】一招攻克CIE高数中最难真题类型！！...

原标题：【A-level高数】一招攻克CIE高数中最难真题类型！！

今天我们讲解一道CIE Further Mathematics Paper1 2018年的真题，值得一提的是本题中将需要把同样的一个知识点反复使用，考察了学生能否透彻的理解原理。

■ 首先我们来看题目的内容：

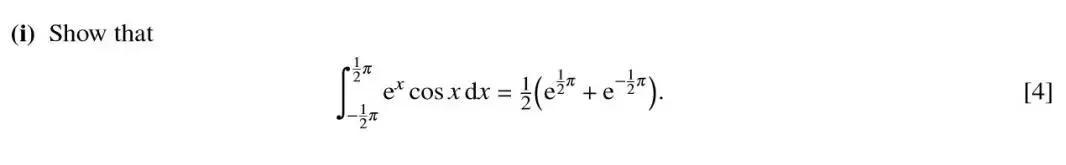
第一问比较明显，需要用到在P3中学习过的Integration by parts的技巧，直接套用公式

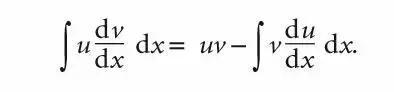
即可得到

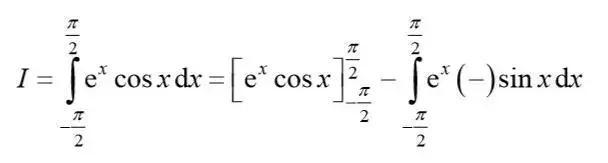
这里需要再次用到Integration by parts的技巧，将后面的式子化回到Ⅰ的形式

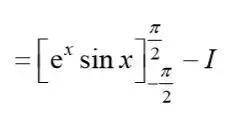
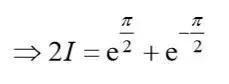
等式两边都除以2后可得到所需结果，注意在本题中，第一次Integration by parts时，无论是假设

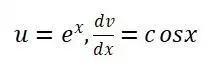
或是

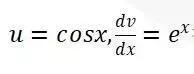
都可以继续进行，只要再次Integration by parts后把后面的式子化成Ⅰ的表达式即可。

■ 接下来是第二题，所占分值最重(6分)，因此也是最复杂的一题。

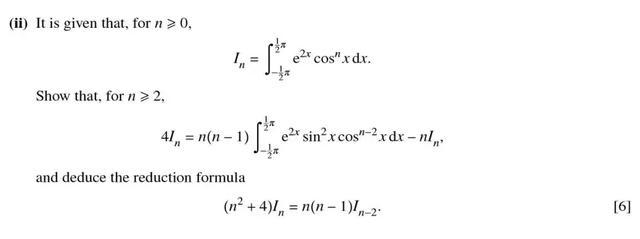
我们注意到，所需要证明的式子仍然是Ⅰ的表达式，所以我们还是需要用在FP2中学到的Integration using reduction formulae。

而这个技巧其实就是反复使用Integration by parts。这次所需的表达式中cosx的指数从原式中的n变为了n-2，所以我们要将cosx进行微分，在Integration by parts的公式中将

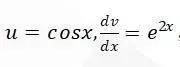
代入后，我们将得到如下式子：

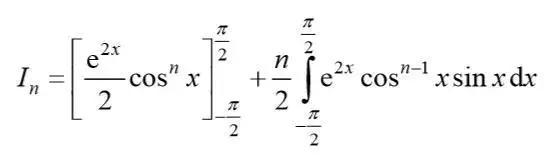
用同样的方法再次积分，我们将得到：

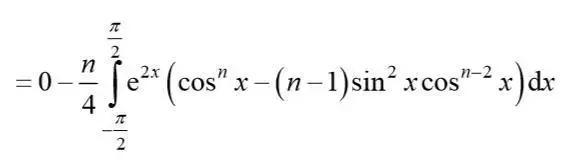
化简后，等式两边都乘以4即可得到所需结果

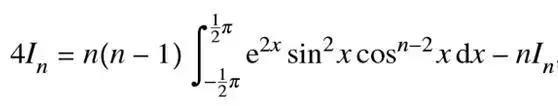
证明完第一部分，我们需要继续化简该式子来得到第二部分的内容。

注意到，所需答案中的三角函数部分都被化简了，因此我们需要从最好化简的

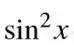
入手，利用公式

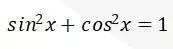
可得

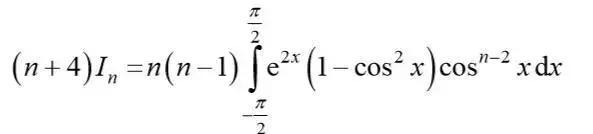
注意到右半部分等式的积分部分可化为

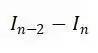
所以

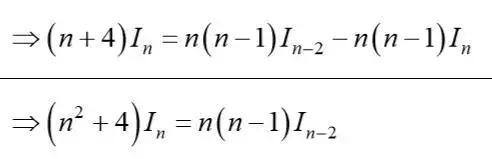
证明完毕。

■ 第三问中，题目已经告诉我们需要使用第一部分和第二部分的结果来解题。那么题目中的

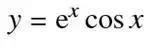
我们可以化成第二问中的Ⅰ的表达式，即

再结合第二问的结果，我们将得到

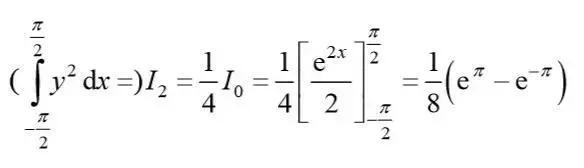
我们需要根据这个结果算出y的平均值

以上就是本次的真题讲解了，比较明显的一个特点是本题中所需的知识点并不太多，但需要大量的Integration计算，稍不留神就可能出错。

责任编辑：