朴素贝叶斯(NBM)之后验概率最大化的含义 | 统计学习方法

朴素贝叶斯 - 贝叶斯估计Python复现：

[舟晓南：朴素贝叶斯（Bayes）模型python复现 - 贝叶斯估计；下溢出问题]

在《统计学习方法》一书中，详细说明了后验概率最大化与期望风险最小化之间的关系，深入地说明了后验概率最大化的含义，但其中的推导过程有所省略，这篇文章作为补充说明。

后验概率最大化的含义：

书中提到，朴素贝叶斯法将实例分到后验概率最大的类中，这等价于期望风险最小化。

要明白什么是期望风险最小化，首先要明白什么是期望。

期望是指某件事大量发生后的平均结果，反应了随机变量平均取值的大小。计算期望的公式：

 
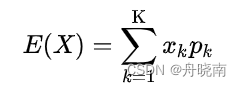
其中x为X的取值，p为在X为该取值的概率，K为x可取值的数量。

期望与平均值之间的关系：

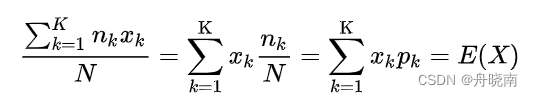ter)

 
其中N是实例总数，n是X为x取值时的实例数量。

举个例子，在10户人家中有3户拥有1个孩子，有3户拥有2个孩子，有4户拥有3个孩子，则其期望为：

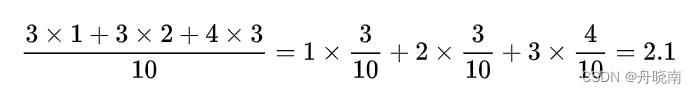
即对家庭的期望是每个家庭有2.1个孩子。

说回期望风险，按照书中的定义，期望风险的含义是：模型关于联合分布的期望损失，学习的目标就是选择期望风险最小的模型。

既然期望风险就是期望损失，那么我们需要定义一个损失函数，用来判断模型的好坏。

假设我们在朴素贝叶斯分类器中使用0-1损失函数：

 
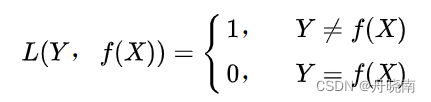
其中f(X)就是习得的朴素贝叶斯模型。

那么期望风险代表的就是损失的平均值，函数为：

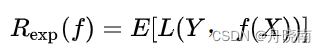
因为期望的定义是值出现的概率乘以具体值之和，所以上式可转换为损失函数与联合概率之积的积分：

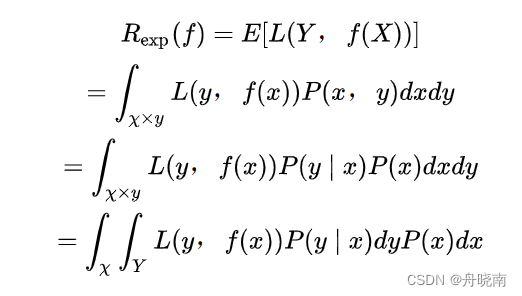
在上式的转换中运用了联合概率，边缘概率和条件概率的关系。
我们设 为H(x)。

H(x)中损失函数大于等于0，条件概率P(y|x)大于0，因此H(x)大于0。同时P(x)也大于0，且当X=x时P(x)（先验概率）为常数，因此期望风险最小化可转换为条件期望最小化，即argminH(x)

 
上式的第二个等式成立，是因为损失函数表示当分类错误时取1，那么我们只需要最小化分类错误的概率，也就是最小化 。

上式最后推导出在朴素贝叶斯分类器中，期望风险最小化等价于后验概率最大化。

同名公众号和知乎：舟晓南

对机器学习，深度学习，python感兴趣，欢迎关注专栏，学习笔记已原创70+篇，持续更新中~ ^_^

学习笔记：数据分析，机器学习，深度学习​https://www.zhihu.com/column/c_1274454587772915712

专栏文章举例：

【机器学习】关于逻辑斯蒂回归，看这一篇就够了！解答绝大部分关于逻辑斯蒂回归的常见问题，以及代码实现 - 知乎 (zhihu.com)

关于 python 二三事​https://www.zhihu.com/column/c_1484952401395941377

专栏文章举例：

记录一下工作中用到的少有人知的pandas骚操作，提升工作效率 - 知乎 (zhihu.com)

关于切片时不考虑最后一个元素以及为什么从0开始计数的问题 - 知乎 (zhihu.com)

关于转行：

舟晓南：如何转行和学习数据分析 | 工科生三个月成功转行数据分析心得浅谈

舟晓南：求职数据分析师岗位，简历应该如何写？｜工科生三个月成功转行数据分析心得浅谈

我建了个数据分析，机器学习，深度学习的群~ 需要学习资料，想要加入社群均可私信~

在群里我会不定期分享各种数据分析相关资源，技能学习技巧和经验等等~

详情私信，一起进步吧！