[huffman tree] fast_wpl带权路径长度的快速计算

wpl: weighted path length，指带权路径长度。

        要解出一组权值对应huffman树的带权路径长度，最直接的做法是先构造出huffman树，然后计算所有叶子结点的带权路径之和，即：

        这种解法需要我们先构造出huffman树，然后标记每个叶子结点对应的深度，再遍历所有的叶子节点。

        但实际上，如果只需要求解wpl，我们并不需要构造huffman树，更不需要求解深度，遍历叶子节点。只需要反复对原节点及新生成的节点的最小权值进行反复加和即可。

先给出代码：(默认权值数组有序)

//默认权重数组w已经有序(从小到大)
//指针p指向当前最小权值的index，初始值给1
//n为数组w的规模
//权重数组w默认1为起始位
int ans=0;
int fastwpl(int w[],int p,int n)   
{if(n<=1) return 0;        //没有或只有一个节点，wpl为0;if (p>= n) return ans;    //当p指向最末位(根节点),求解结束else {int new_w = w[p] + w[p+1];  //取出两个最小权值，生成新权值ans += new_w;               //插入新权值节点////查找插入位置int i = p+2;        //由于两个最小权值已取出，所以从p+2开始检索while (new_w > w[i] && i<=n ) i++;//在i之前插入新权值for (int j = p + 1; j < i-1; j++) w[j] = w[j + 1];w[i - 1] = new_w;//指针后移一位(每次运算，删除两个最小节点，生成一个新节点，故p+1)p++;fastwpl(w, p, n);}
}

算法说明（以下图huffman树为例)：                 

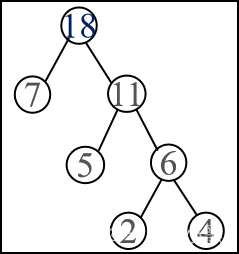
最直接的解法为：

本文解法为：

                ​​​​​​​        ​​​​​​​        ​​​​​​​        

即将所有非根节点权重进行加和。

        这个解法看似不可理喻，它好像完全没考虑节点的路径长度。实际上，“路径长度”，即叶子深度的计算被蕴含在对中间节点的反复求和过程中。

如：节点2、4的路径长度为3，即其带权路径长为2*3+4*3，相当于对2和4反复相加了3次。

        换种思路，当我们对由 2 + 4 构成的新节点 6 进行相加时，也相当于对进行了一次+2+4运算。

即+2+4+6=+2+4 +（2+4) = + 2 * 2 + 4 * 2。

        同样，下一层运算，对6 + 5 得到的新节点11进行相加，相当于又对 6 = 2 + 4进行了一次加和。

        因此在对新节点进行不断加和的过程，相当于不停在迭代叶子节点2和4的路径长度。

具有普遍性的，我们可以得出结论：

       wpl=生成huffman树的所有非根节点权值之和

        由此，要计算一组权值的最小加权路径长度，我们只需要不停迭代相加叶子节点及其新生成的权值节点即可。在权值数组有序情况下，复杂度为O(n);

        至于排序，我们可以使用快排或归并排序。