功能性模块：（10）Spearman‘s rank correlation coefficient的简单理解(含与PCC之间的区别)

Spearman’s rank correlation coefficient的简单理解

1. 背景

在统计学中，斯皮尔曼等级相关系数（Spearman’s rank correlation coefficient， 或者Spearman’s $\rho$， 通常使用$\rho$或者$r_s$来表示），是一个等级相关性的非参数度量（两个变量等级之间的统计相关性）。这个相关系数使用单调函数来描述两个变量之间的关系程度。

如果两个变量的Spearman correlation和Pearson correlation相等，Person correlation评估两组变量的线性关系，Spearman correlation评估的是两组变量的单调性关系（无论是否线性）。如果没有重复的数据值，每个变量都是另外一个变量的完美单调函数时，会出现+1或者-1的完美Spearman correlation。

直观上来看，如果两个变量之间具有相似的等级（或者换句话说完全相同的等级，那么相关性就为1），相似的情况下相关性也会比较高，如果两个变量具有不同的等级（或者完全相反的情况下，那么相关性就为-1），相关性就会非常低。

那么Spearman’s coefficient适用于连续序数变量或者离散序数变量的相关性表示

2.定义

Spearman’s rank correlation coefficient被定义成等级变量之间的Pearson coefficient。

对于样本容量为n的样本，将n个原始数据$X_i$,$Y_i$转换成等级数据$r{g}_{X_i}$,$r{g}_{Y_i}$，并且$r_s$可以按照如下的公式进行计算

$r_s={\rho }_{r{g}_{X_i},r{g}_{Y_i}}=\frac{cov(r{g}_X,r{g}_Y)}{{\sigma }_{r{g}_X}{\sigma }_{r{g}_Y}}$

其中$\rho$表示的是Pearson correlation coefficient（PCC），但是使用的变量是转换成等级后的变量。
$cov(r{g}_X,r{g}_Y)$是转换成等级变量之间的协方差

${\sigma }_{r{g}_X}$, ${\sigma }_{r{g}_Y}$是转换成等级变量后的标准差

只有当所有n个等级都是不同的整数是，才可以使用下面的公式进行计算
$r_s=1-\frac{6\sum d_i^2}{n(n^2-1)}$

其中$d_j=rg(X_i)-rg(Y_i)$是两个变量值等级之间的差异

3.代码实现

很简单的代码实现

def ComputeRs(a, b):aa = np.column_stack((a, b))# rank的方式有很多种，这里使用的average的方式aa_ranked = np.apply_along_axis(stats.rankdata, 0, aa)rs = np.corrcoef(aa_ranked, rowvar=0)return rs[1, 0]

4. Spearman‘s rank correlation coefficient 与Pearson Correlation coeffiicient的区别

最主要的区别是：

• Pearson Correlation coeffiicient是关注的两组数据的线性相关性
• Spearman‘s rank correlation coefficient 是关注两组数据的单调性，换句话说是两组数据的趋势

4.1 线性正相关

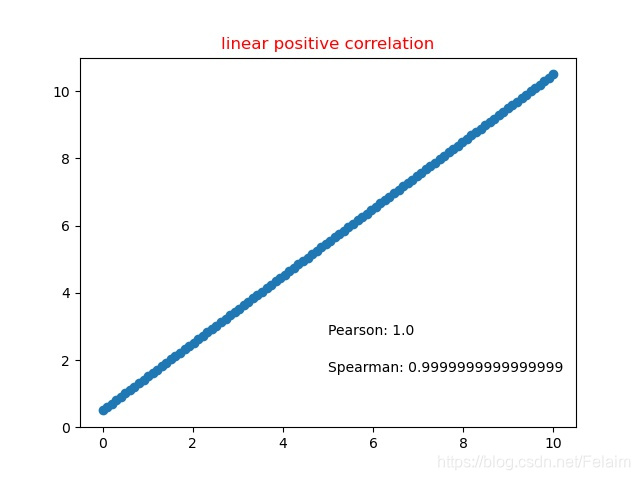
4.2 线性负相关

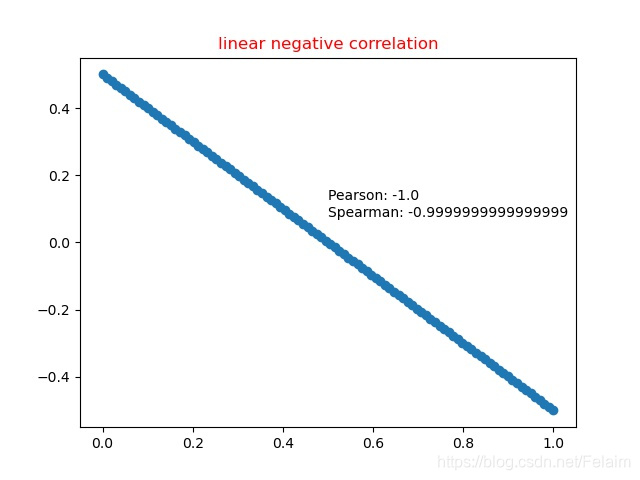
4.3 非线性函数（Sigmoid）

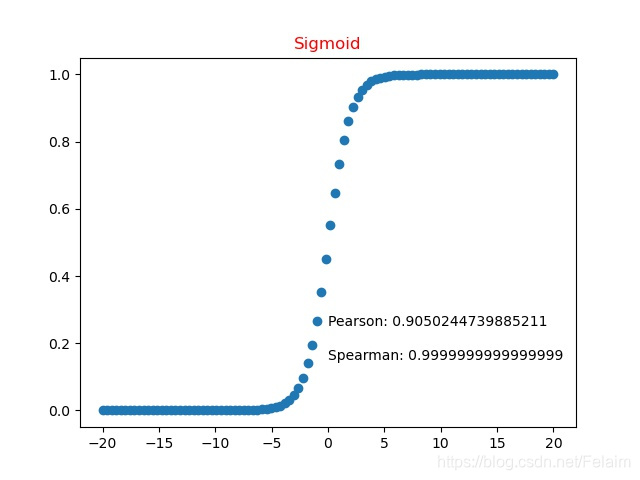
可以看到Spearman还是相关性几乎为+1

4.4 非线性函数（二次函数）

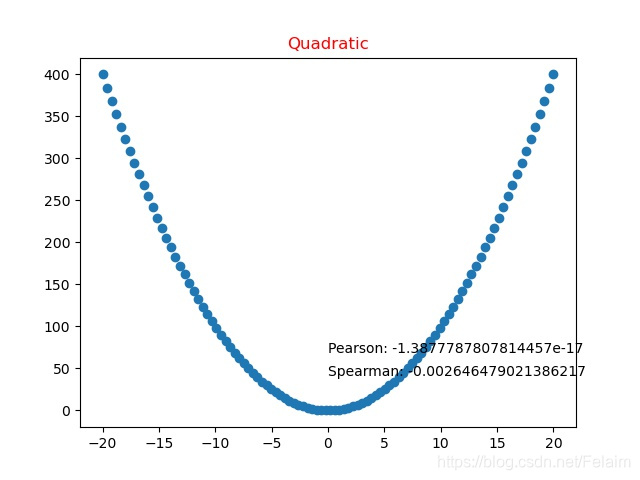
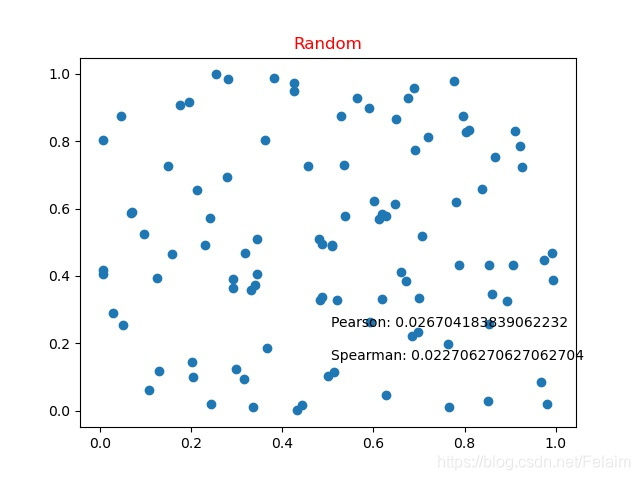
4.5 随机数

4.6 异常值

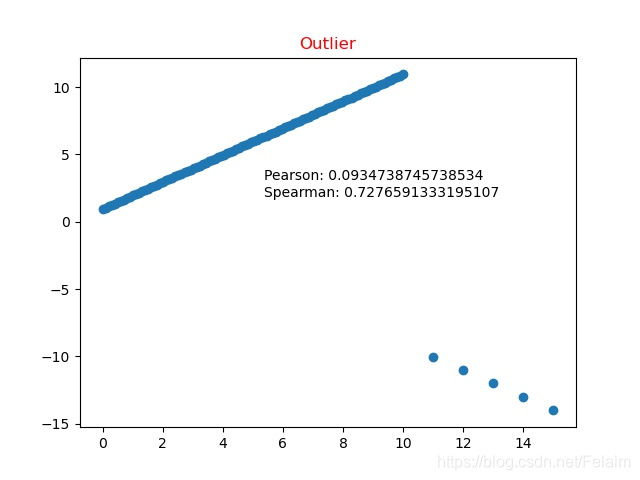
总结，从4.6上可以看出，一旦数据存在异常值，那么Spearman‘s rank correlation coefficient的鲁棒性会更好一些。